http://www.ab126.com/Geography/3753.html
互相变换:
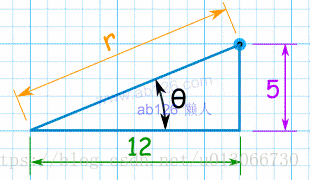
将直角坐标(x,y)转为极坐标(r,θ)
-
r = √( x2+y2)
-
θ = tan-1 (y/x)
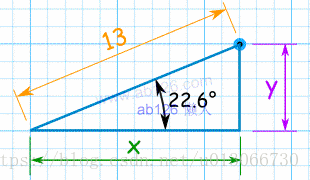
将从极坐标(r,θ)转为直角坐标(x,y)
-
x = r × cos( θ )
-
y = r × sin( θ )
直角坐标系是正方形网状,极坐标系是圆辐射形;
一个直角坐标对应唯一点,一个极坐标也对应唯一点;
但一个点在直角坐标系中的直角坐标是唯一的,
而一个点在极坐标系中的极坐标却有无数多个。





 本文详细介绍了直角坐标系与极坐标系之间的转换公式,包括如何将直角坐标(x,y)转换为极坐标(r,θ),以及如何进行逆向转换。文章指出,尽管一个点在两种坐标系中都有唯一对应,但在极坐标系中,一个点可能有无数个表示方式。
本文详细介绍了直角坐标系与极坐标系之间的转换公式,包括如何将直角坐标(x,y)转换为极坐标(r,θ),以及如何进行逆向转换。文章指出,尽管一个点在两种坐标系中都有唯一对应,但在极坐标系中,一个点可能有无数个表示方式。
















 1万+
1万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








