一、絮絮叨叨
计划写一系列数据结构与算法的博客:
- 一是给自己立个flag——坚持做完,
- 二是记录自己的学习过程,总结和分享知识
1、Why?
- 面试 =》考查基础 =》数据结构与算法
- 工作 =》有助于理解、使用框架;优化程序,提升效率、性能
- 锻炼逻辑思维能力 =》提升个人竞争力
2、What?
数据结构: Array(数组)、Stack/Queue(堆栈/队列)、PriorityQueue(优先队列)、LinkedList(链表)、Tree/Binary Search Tree(树/二分查找树)、HashTable(哈希表、散列表)、Disjoint Set(并查集)、Heap(堆)、跳表(SkipList)、Trie、BloomFilter、LRU Cache
算法: Greedy(贪婪算法)、Recursion/Backtrace(递归/回溯)、Traversal(遍历)、Breadth-first/Depth-first search(广度优先/深度优先搜索)、Divide and Conquer(分治法)、Dynamic Programming(动态规划)、Binary Search(二分查找)、Graph(图)、sort(排序)、字符串匹配算法、哈希算法
3、How?
(1)Chunk it up(切碎知识点)==》从书籍、课程中获得
(2)Deliberate practicing(刻意练习)
+ 刻意练习:练习缺陷、弱点的地方
+ 心理:感觉不舒服、不爽、枯燥 =》坚持住
(3)Feedback(反馈)
+ ① 即时反馈
+ ② 主动型反馈(自己去找)
+ 高手代码(Github、LeetCode…)
+ 论坛交流
+ ③ 被动式反馈(高手指点)
+ code review
+ 高手看自己打并给予反馈
4、关键点
- 来历、自身的特点、适用解决的问题、实际应用场景
5、解题步骤
(1) 理解题目
(2)想出 possible solutions
- 关注时间/空间复杂度
- 选择最优解法
(3) Coding!!!
(4)测试多种情况下,检查codes是否考虑周全
6、相关书籍
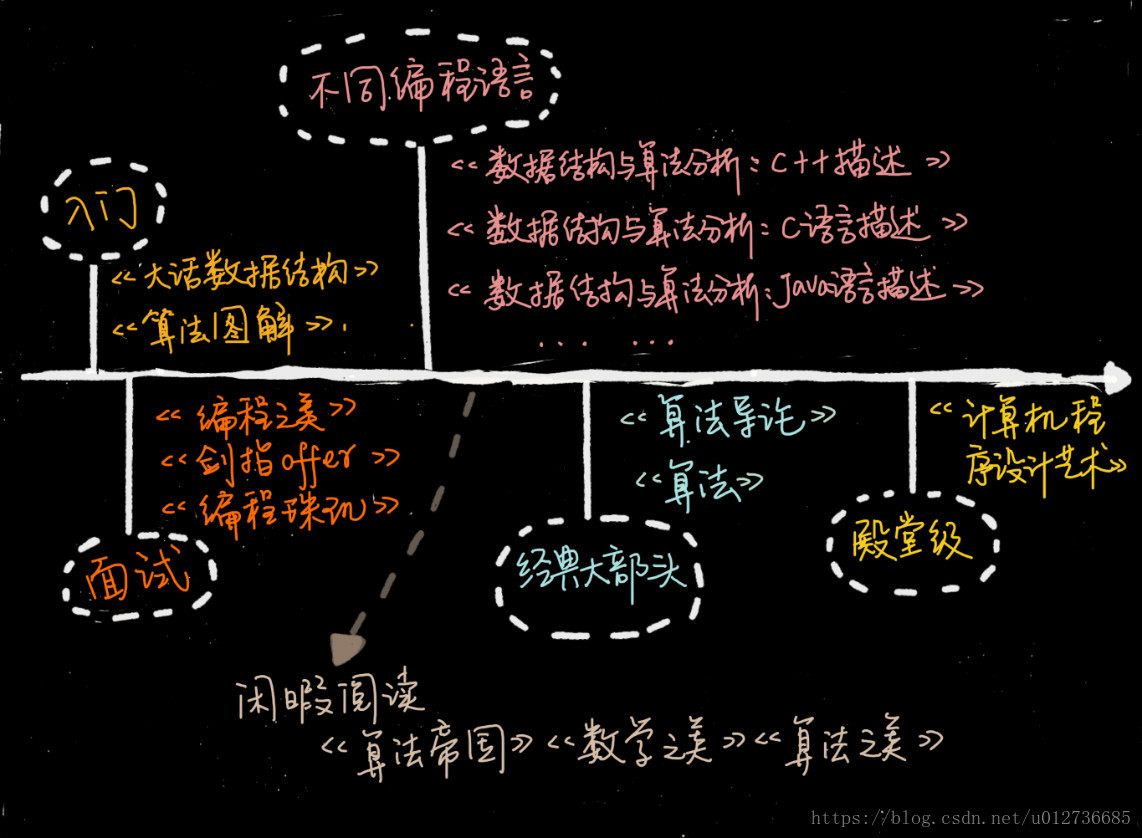
一、数据结构
1、概念
数据结构:是相互之间存在一种或多种特定关系的数据元素的集合 =》存储结构
算法:是为求解一个问题需要遵循的、被清楚地指定的简单指令的结合。
两者关系: 数据结构为算法服务,算法作用于数据结构之上。
二、复杂度分析
- 时间/空间复杂度 ——是效率和资源消耗的度量衡(不依赖于环境)
1、大O时间复杂度表示法
- 所有代码的执行时间 T(n) 与每行代码执行的次数 n 成正比 ==》可用执行的次数衡量算法的优劣
T(n) = O(f(n))=》 大O记法
其中,T(n)表示代码执行的时间,n表示数据规模的大小,f(n)表示每行代码执行次数的总和。
大O时间复杂度实际上并不具体代表代码真正的执行时间,而是代表代码执行时间随数据规模增长的变化趋势,所以,也叫做渐进时间复杂度。
2、时间复杂度分析
- 只关注循环执行次数最多的一段代码
- 加法法则:总复杂度等于量级最大的那段代码的复杂度
若 T1(n) = O(f(n)), T2(n) = O(g(n)),
则 T1(n) = T1(n) + T2(n) = max(O(f(n)), O(g(n))) = O(max(f(n), g(n)))
- 乘法法则:嵌套代码的复杂度等于嵌套内外代码复杂度的乘积
3、几种常见时间复杂度
(1)多项式量级
- O(1)——常数复杂度(Constant Complexity)
int i = 10;
int j = 6;
int sum = i + j;
- O(logn) ——对数复杂度
for(int i = 1; i < n; i = i * 2){
cout<<"Hey~I'm busy looking at:"<<i<<endl;
}
- O(n)——线性复杂度
for(int i = 1; i <= n; i++){
cout<<"Hey~I'm busy looking at:"<<i<<endl;
}
- O(nlogn)——线性对数阶
- O(nlogn) 也是一种非常常见的算法时间复杂度。比如,归并排序、快速排序的时间复杂度都是 O(nlogn)。
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j = j * 2){
cout<<"Hey~I'm busy looking at:"<<i<<"and"<<j<<endl;
}
}
- O(n2)、O(n3) … O(nk)——平方阶、立方阶…k次方阶
// 平方阶复杂度
for(int i = 1; i <= n; i++){
for(int j = 1; j <= m; j++){
cout<<"Hey~I'm busy looking at:"<<i<<"and"<<j<<endl;
}
}
//k次方阶复杂度
for(int i = 1; i <= Math.pow(2,n);i++){
cout<<"Hey~I'm busy looking at:"<<i<<endl;
}
- O(m+n)、O(m*n)——m和n表示两个数据规模的大小,且无法事先评估m和n的量级大小
(2)非多项式量级
时间复杂度为非多项式量级的算法问题 =》NP(Non-Deterministic Polynomial)问题
- O(2n)——指数阶
- O(n!)——阶乘阶
for(int i = 1; i <= factorial(n); i++){
cout<<"Hey~I'm busy looking at:"<<i<<endl;
}
4、空间复杂度分析
空间复杂度表示算法的存储空间与数据规模之间的增长关系,又称渐进空间复杂度。
常见的空间复杂度:O(1)、O(n)、O(n2)
void print(int n){
int i = 0;
int *a = new int[n];
for (i; i<n; ++i){
a[i] = i * i; }
for (i = n-1; i>=0; --i){
cout<<a[i]<<endl; }
}
第二行代码中,我们申请了一个空间存储变量i,但是它是常量阶的,跟数据规模n没有关系,所以可以忽略。第三行中,我们申请了一个大小为n的int类型数据。所以整段代码的空间复杂度就是O(n)。
5、复杂度比较
复杂度从低到高:
O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n3) <… < O(2n) < O(n!)

三、其他时间复杂度
1、最好/最坏情况时间复杂度(best/wrost case time complexity)
// 目的:在一个无序的数组中,查找变量x出现的位置
// n 表示数组 array 的长度
int fun1( int[] array, int n, int x){
int i = 0;
int pos = -1;
for(; i < n, ++i){
//找到即结束
if( array[i] == x) {
pos = i;
break;
}
}
return pos;
}
复杂度分析:变量 x 可能出现在数组中的任何位置。如果数组中第一个元素正好是要查找的变量 x ,那就不需要遍历剩下的 n-1 个数据了,这时时间复杂度为 O(1) ,也就是最好情况时间复杂度为 O(1)。 但如果数组中不存在变量 x ,那么就需要把整个数组都办理一遍,时间复杂度就是 O(n) ,也就是最坏情况时间复杂度为 O(n)。 所以不同情况下,这段代码的时间复杂度是不一样的。
==》引入概念:最好情况时间复杂度、最坏情况时间复杂度、平均情况时间复杂度。
2、平均情况时间复杂度
平均情况时间复杂度:假定各种输入实例的出现符合某种概率分布(如均匀独立随机分布)之后,进而估计出的加权平均时间复杂度
复杂度分析: 仍为上面的例子,要查找的变量x,要么在数组里,要么不在数组里。这两种情况对应的概率统计起来很麻烦,假设这两种情况的概率都为1/2。要查找的数据在0~n-1这n个位置的概率也是一样的,为1/n。所以根据概率乘法法则,要查找的数据出现在0~n-1中任意位置的概率为1/2n。
把每种情况发生的概率也考虑上:
1*1/2n + 2*1/2n + 3*1/2n + ... + n*1/2n + n*1/2 = (3n+1)/4
==》平均情况时间复杂度为O(n)
3、均摊时间复杂度
(1)举例
目的:数组元素求和(有限大小)——往数组中插入数据,当数组满后count = n,用for循环遍历数组求和,并清空数组。求和之后的sum值当道数组的第一个位置,然后再进行插入,如果数组一开始就有空闲空间,直接插入。
int arr[SIZE] = {0};
int n = sizeof(arr)/sizeof(arr[0]);
int count = 0;
int fun2(int val)
{
if(count == n)
{
int sum = 0;
for(int i=0; i<n; i++)
{
sum = sum + arr[i];
}
arr[0] = sum;
count = 1;
}
arr[count] = val;
++count;
}
最好情况时间复杂度:O(1)
最坏情况时间复杂度:O(n)
平均时间复杂度: 假设数组的长度是n,根据数据插入位置的不同,我们可以分为n种情况,每种情况的时间复杂度为O(1)。除此外,还有一种情况,就是当数组没有空闲空间时,这时的时间复杂度为O(n)。而且,这n+1种情况发生的概率一样,都是1/(n+1)。所以有:
1*1/(n+1) + 1*1/(n+1) + ... + 1*1/(n+1) + n*1/(n+1) = O(1)
(2)对比 fun1( ) 与 func2( ):
- fun1函数在极端情况下,复杂度才为O(1)。但是fun2在大部分情况下,时间复杂度都为O(1),只有个别情况下,复杂度才比较高。
- 对于fun2来说,O(1)时间复杂度的插入和O(n)时间复杂度的插入的出现是有规律的,而且有一定的前后时序关系,一般是O(n)插入后,紧跟着n-1个O(1)的插入操作,循环往复。
均摊时间复杂度: 在代码执行的所有复杂度情况中绝大部分是低级别的复杂度,个别情况是高级别复杂度且发生具有时序关系时,可以将个别高级别复杂度均摊到低级别复杂度上。基本上均摊结果就等于低级别复杂度。
上例分析:对于每一次的O(n)操作,将时间均摊给n-1个O(1)的操作,这样均摊下来,总的时间复杂度为O(1)。==》func2()的均摊时间复杂度为O(1)
四、递归算法的时间复杂度
待补充。。。
























 5226
5226

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








