线性数据结构——链表、堆栈和队列
二叉树严格控制了每个结点最多只能有两个后继结点(简称“儿子”)控制了这样的结构之后,这棵树就比普通的树简单很多
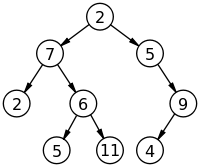
我们再用二叉树来做点有意义的事情,比如说保持结构里面结点的大小顺序等等,于是我们就有一个更实用的树结构:二叉查找树(Binary Search Tree)

在二叉树的基本定义上,二叉查找树有一层更深的定义:左儿子的元素大小严格小于父结点,右儿子的元素大小严格大于父结点。这样的话,进行搜索的时候,从根结点出发,如果想要找的元素比这个结点小,向左搜,否则向右搜。这样的搜索效率竟然可以控制到平均O(log n)!实在是太快了!
不过,O(log n)的效率仅限于一棵比较随机的二叉查找树,如果一棵二叉查找树,儿子永远比父亲大,那么就会变成一条直线,效率也是只有O(n)而已。那么效率就变得很虚无飘渺了。
幸好,伟大的计算机科学家们在二叉查找树的基础上,加上了自动平衡的算法,因此创造出AVL树(AVL Tree):
最佳二叉排序树通常用于存储构造后就不经常改动的静态字典;对于动态字典,在进行元素的插入和删除操作时,为了能够较快地对二叉排序树进行调整,通常不要求二叉排序树调整到“最佳的”检索效率,而是希望达到“较佳”的状态。
保持二叉排序树平衡的一个有效方法,即构造平衡二叉排序树,又称AVL树。平衡二叉排序树具有下列性质∶每个结点左、右子树深度之差的绝对值不超过1。结点右子树深度与左子树深度之差定义为该结点的平衡因子,平衡二叉排序树中每个结点的平衡因子只能是1、0或-1。
n个结点的AVL树的高度一定是O(log n)
检索,插入,删除的效率是O(log 2 n)
适用于组织较小的,内存中的目录

AVL树的平衡条件是:左儿子高度与右儿子高度相差不超过1,上图则是给出了平衡算法。告诉大家该怎么样对树进行旋转,而得到一棵新的平衡树。
AVL树的效率已经非常可观了,平衡之后整棵树的访问效率为O(log n),插入移除效率O(log n),可谓十分迅速!
但是人们总是不知足的,与其通过分析树本身结构来调整,倒不如自己创建标记,再根据标记来调整,减少旋转次数!于是红黑树(Red Black Tree)就此诞生:

hash表:
hashing定义了一种将字符组成的字符串转换为固定长度(一般是更短长度)的数值或索引值的方法,称为散列法,也叫哈希法。由于通过更短的哈希值比用原始值进行数据库搜索更快,这种方法一般用来在数据库中建立索引并进行搜索,同时还用在各种解密算法中。
堆:
堆特点:堆顶元素是整个序列最大或者最小的元素。
堆排序:
堆排序例题:























 13万+
13万+

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








