1381 - Balancing the Scale (技巧枚举+位运算)

最新推荐文章于 2019-08-23 11:25:42 发布

lab104_yifan

最新推荐文章于 2019-08-23 11:25:42 发布

阅读量1.8k

点赞数 2

CC 4.0 BY-SA版权

分类专栏：算法竞赛入门经典训练指南-第一章暴力-技巧枚举高效算法-位运算

本文链接：https://blog.youkuaiyun.com/accelerator_/article/details/18945155

算法竞赛入门经典训练指南-第一章同时被 3 个专栏收录

181 篇文章

订阅专栏

暴力-技巧枚举

22 篇文章

订阅专栏

高效算法-位运算

15 篇文章

订阅专栏

本文探讨了一种使用特定算法解决平衡具有独特方程的天平问题的方法，包括问题描述、输入输出规范、详细解题策略及代码实现。重点在于通过位运算技巧和全排列算法来计算不同组合的数量。

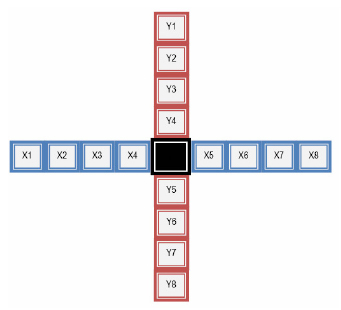
You are given a strange scale (see the figure below), and you are wondering how to balance this scale. After several attempts, you have discovered the way to balance it -- you need to put different numbers on different squares while satisfying the following two equations:

x₁ * 4 + x₂ * 3 + x₃ * 2 + x₄ = x₅ + x₆ * 2 + x₇ * 3 + x₈ * 4

y₁ * 4 + y₂ * 3 + y₃ * 2 + y₄ = y₅ + y₆ * 2 + y₇ * 3 + y₈ * 4

How many ways can you balance this strange scale with the given numbers?

Input

$\epsfbox{p3693.eps}$

There are multiple test cases in the input file. Each test case consists of 16 distinct numbers in the range [1, 1024] on one separate line. You are allowed to use each number only once.

A line with one single integer 0 indicates the end of input and should not be processed by your program.

Output

For each test case, if it is possible to balance the scale in question, output one number, the number of different ways to balance this scale, in the format as indicated in the sample output. Rotations and reversals of the same arrangement should be counted only once.

Sample Input

87 33 98 83 67 97 44 72 91 78 46 49 64 59 85 88 
0

Sample Output

Case 1: 15227223

题意：给定16个数字，求题目中给定公式的平衡方法有几种

思路：技巧枚举+位运算，通过位运算每次枚举4个数字，通过全排列求出和，算出2边相同时候状态的种数，最后在把x的情况和y的情况数相乘并所有都相加就是答案，计算全排列前要排序一开始忘了答案一直少，后面看了题解才发现。一开始还理解错题目了以为x和y的和都是要相同的。

代码：

#include <stdio.h>
#include <string.h>
#include <vector>
#include <algorithm>
using namespace std;

int num[16], st[16], Sum[(1<<16)];
vector<int> sum[22222];

bool judge(int state) {
	int sn = 0;
	for (int i = 0; i < 16; i++) {
		if (state&(1<<i))
			st[sn++] = num[i];
	}
	if (sn == 4) return true;
	return false;
}

int solve() {
	int ans = 0;
	memset(sum, 0, sizeof(sum));
	memset(Sum, 0, sizeof(Sum));
	sort(num, num + 16);
	for (int i = 0; i < (1<<16); i++) {
		if (judge(i)) {
			do {
				int s = st[0] * 4 + st[1] * 3 + st[2] * 2 + st[3];
				for (int j = 0; j < sum[s].size(); j++) {
					if ((i&sum[s][j]) == 0)
						Sum[(i|sum[s][j])]++;
				}
				sum[s].push_back(i);
			} while(next_permutation(st, st + 4));
		}
	}
	for (int k = 0; k < (1<<16); k++)
		ans += Sum[k] * Sum[k^((1<<16)-1)];
	return ans / 2;
}

int main() {
	int cas = 0;
	while (~scanf("%d", &num[0]) && num[0]) {
		for (int i = 1; i < 16; i++)
			scanf("%d", &num[i]);
		printf("Case %d: %d\n", ++cas, solve());
	}
	return 0;
}