决策树

一.决策树的构建

决策树的构建主要是确定各个节点的排放顺序。排放顺序的的策略：这里有信息增益，增益比，基尼系数这3种。

所以说信息增益，增益比，基尼系数决定着决策树的划分。选择信息增益最大的属性，作为根节点，依次递归排列。

二.熵和信息熵

通常使用“熵”来度量样本集合的纯度，“熵”就是物体内部的混乱程度，理论上“熵”的值越小，数据集的“纯度”越高，下面是“熵”的计算公式：

• Pk指的是第k类样本所占的比率。

信息熵：指的是测试属性对于样本纯度的增益效果，值越大越好，计算公式为： 

• 信息增益=样本的熵-所有测试属性熵的和
• Dv指的是满足某个测试属性的样本集。

选择信息增益最大的属性，作为根节点，然后递归计算最优的节点属性即可组成最优的策略树。ID3算法就是依此实现的。

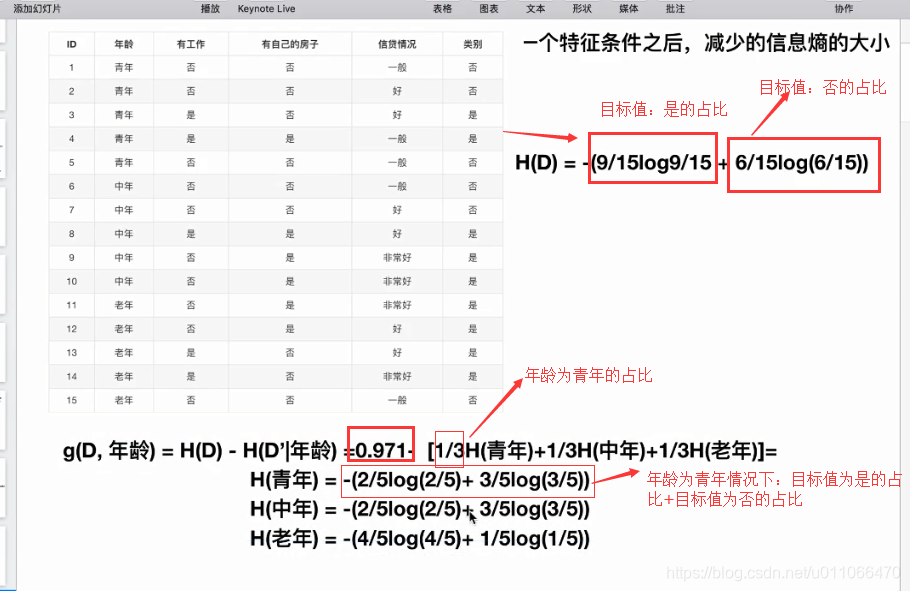
同样道理求出特征：工作，年龄，贷款特征的增益，g（D，a4）=0.4，最大，选择a4特征最为最佳特征，先放到树的第一个节点上，依次递归计算。

三. 剪枝处理
构建决策树的过程中，如果完全按照训练集进行分支节点的构建，会使决策树与训练集过拟合，无法支持真实数据的要求，而且由于分支节点过多，还会增大训练和测试的时间开销。为了解决这个问题，需要对决策树进行剪枝处理。

是否裁剪，可以依据裁剪前后的精确度来判断。

3.3.1 预剪枝
在生成决策树的过程中，判断每个节点是否需要划分。判断的标准是增加该节点后是否能提升精度。

优点：
- 降低过拟合的风险。
- 降低训练时间和测试时间开销。

缺点：有这种风险，该节点降低了精度，但是子节点可以提升精度，在预剪枝中会丢失。

3.3.2 后剪枝
先生成决策树，然后从底到根对决策树的节点进行裁剪。判断的标准是减少该节点后是否能提升精度。

优点：
- 降低欠拟合的风险。所谓过拟合（over-fitting）就是所建的模型在训练样本中表现得过于优越，导致在验证数据集以及测试数据集中表现不佳；欠拟合则相反，模型在训练集上表现都非常差。
-泛化性能往往优于预剪枝。

缺点：后剪枝需要首先形成一颗完整的树，再从底到根进行判定，会增加训练和测试的开销。

3.4 数据预处理
3.4.1 连续值
连续值的取值范围没有限制，需要转换为离散值才能进行分类任务，一般采用2分法：取一个中间值，小于中间值的为分类a，大于中间值的为分类b。

与离散值不同的是，连续值的属性，可以在子节点中多次使用。

3.4.2 缺失值
缺失值的处理方式，是把包含缺失值的样本，拷贝到各个分类中，只是权重为1/n，n为分类的数目。

后面的计算方式就一样了，计算每个节点的信息增益，判断是否需要划分节点。

https://blog.youkuaiyun.com/u013252773/article/details/87018168?ops_request_misc=%257B%2522request%255Fid%2522%253A%2522158909117519724845039939%2522%252C%2522scm%2522%253A%252220140713.130102334..%2522%257D&request_id=158909117519724845039939&biz_id=0&utm_medium=distribute.pc_search_result.none-task-blog-2~all~baidu_landing_v2~default-2-87018168.nonecase&utm_term=%E5%86%B3%E7%AD%96%E6%A0%91