[数据自习室]第一周-数据的描述性统计

[数据自习室]第一周-数据的描述性统计

数据的集中趋势

**众数：**出现次数最多的数。
**中位数：**按顺序排序，处于中间位置的数。
**平均数：**一般指的是 算术平均数。
**极差：**最大值与最小值之间的差距。

**分位数：**亦称分位点，是指将一个随机变量的概率分布范围分为几个等份的数值点，常用的有中位数（即二分位数）、四分位数、百分位数等。

1.二分位数
对于有限的数集，可以通过把所有观察值高低排序后找出正中间的一个作为中位数。如果观察值有偶数个，则中位数不唯一，通常取最中间的两个数值的平均数作为中位数，即二分位数。

2.四分位数
四分位数（Quartile）是统计学中分位数的一种，即把所有数值由小到大排列并分成四等份，处于三个分割点位置的数值就是四分位数。
1）第一四分位数(Q1)，又称“较小四分位数”，等于该样本中所有数值由小到大排列后第25%的数字；
2）第二四分位数(Q2)，又称“中位数”，等于该样本中所有数值由小到大排列后第50%的数字；
3）第三四分位数(Q3)，又称“较大四分位数”，等于该样本中所有数值由小到大排列后第75%的数字。
第三四分位数与第一四分位数的差距又称四分位差。

3.百分位数
百分位数，如果将一组数据从小到大排序，并计算相应的累计百分位，则某一百分位所对应数据的值就称为这一百分位的百分位数。运用在教育统计学中，例如表现测验成绩时，称PR值。

算术平均数：
算术平均数是指在一组数据中所有数据之和再除以数据的个数。它是反映数据集中趋势的一项指标。

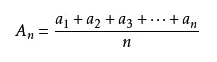
加权平均数：
加权平均数是不同比重数据的平均数，加权