从线性到非线性模型-三层神经网络

从线性到非线性模型

1、线性回归，岭回归，Lasso回归，局部加权线性回归

2、logistic回归，softmax回归，最大熵模型

3、广义线性模型

4、Fisher线性判别和线性感知机

5、三层神经网络

6、支持向量机

五、三层神经网络

一、神经单元

​ 深度学习的发展一般分为三个阶段，感知机–>三层神经网络–>深度学习（表示学习）。早先的感知机由于采用线性模型，无法解决异或问题，表示能力受到限制。为此三层神经网络放弃了感知机良好的解释性，而引入非线性激活函数来增加模型的表示能力。三层神经网络与感知机的两点不同

1）非线性激活函数的引入，使得模型能解决非线性问题

2）引入激活函数之后，不再会有$0$损失的情况，损失函数采用对数损失，这也使得三层神经网络更像是三层多元（神经单元）逻辑回归的复合

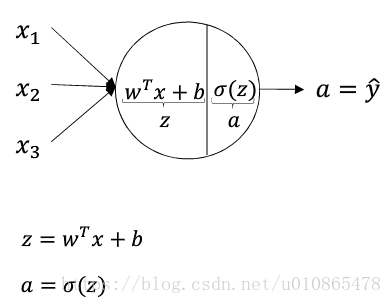
神经网络中每一个神经元都可以看作是一个逻辑回归模型，三层神经网络就是三层逻辑回归模型的复合，只是不像逻辑回归中只有一个神经元，一般输入层和隐藏层都是具有多个神经元，而输出层对应一个logistic回归单元或者softmax单元，或者一个线性回归模型。

这里对一些常用的非线性激活函数做一些简单的介绍（图像，性质，导数）

$$sigmoid(z)=\frac{1}{1+e^{-z}},tanh(z)=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}},relu(z)=max \left\{0,z\right \},leaky relu(z)=\left\{\begin{matrix} \alpha z,z<0\\ z ,z\geqslant 0 \end{matrix}\right.$$
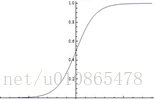
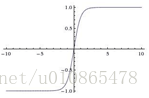
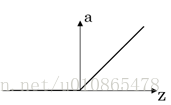
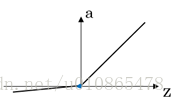
性质：对于以上几个非线性激活函数都可以看作是 $\left\{\begin{matrix} 0,z<0\\ 1,z\geqslant 0\end{matrix}\right.$ ，的一个近似。采用近似的一个重要原因是为了求导，早起常采用平滑的sigmoid和tanh函数，然而我们可以发现这两个函数在两端都存在导数极小的情况，这使得多层神经网络在训练时梯度消失，难以训练。而Relu函数则很好的解决两端导数极小的问题，也是解决神经网络梯度消失问题的一种方法。

导数：

sig(z)=11+e−z,d(z)=−−e−z(1+e−z)2=e−z+1(1+e