http://acm.fzu.edu.cn/problem.php?pid=2020
注意要用64位数据类型,一开始一直被wrong!!!
#include <stdio.h>
typedef __int64 LL;
LL PowMod(LL base,LL n,LL m)
{
LL res = 1;
while(n)
{
if(n&1)
res = res*base%m;
base = base*base%m;
n >>= 1;
}
return res;
}
LL Cal(LL n,LL m,LL p)
{
LL res = 1,re;
for(LL i = 1;i <= m;++i)
{
res = res*(n-i+1)%p;
re = PowMod(i,p-2,p);
res = res*re%p;
}
return res;
}
LL Lucas(LL n,LL m,LL p)
{
if(n < m)
return 0;
else
return Cal(n,m,p);
}
int main()
{
int T;
scanf("%d",&T);
while(T--)
{
LL n,m,p;
scanf("%I64d%I64d%I64d",&n,&m,&p);
LL res = 1;
while(n||m)
{
int a = n%p;
int b = m%p;
n = n/p;
m = m/p;
res = (res*Lucas(a,b,p));
if(res == 0)
break;
}
printf("%I64d\n",res);
}
return 0;
}
注意在使用Lucas的时候要p为质数的时候才成立,否则不能使用。
之后再介绍一下Lusca算法吧!
Lucas定理,设p是一个素数(题目中要求取模的数也是素数),将n,m均转化为p进制数,表示如下:
满足下式:
即C(n,m)模p等于p进制数上各位的C(ni,mi)模p的乘积。利用该定理,可以将计算较大的C(n,m)转化成计算各个较小的C(ni,mi)。
该方案能支持整型范围内所有数的组合数计算,甚至支持64位整数,注意中途溢出处理。该算法的时间复杂度跟n几乎不相关了,可以认为算法复杂度在常数和对数之间。
【卢卡斯(Lucas)定理】
Lucas定理用来求C(a,b)mod p的值,其中p为素数。
数学表达式为:
Lucas(a,b,q)=C(a%q,b%q)*Lucas(a/p,b/p,p);
Lucas(a,0,q)=0;
通过这个定理就可以很方便的把大数的组合转化成小数。但其中还是要求C(a%q,b%q)%p,所以这里引入逆元来求。
【定义】若整数a,b,p, 满足a·b≡1(mod p).则称a 为b 模p 的乘法逆元, 即a=b- 1mod p.其中, p 是模数。
应用到组合数中来就是:
a!/[b!*(a-b)!] % p == a! * [b!*(a-b)!]-1 %p
【逆元求法】:
应用费马小定理,ap-1=1 mod p ,即 a*ap-2=1 mod p
也就是说 ap-2就是a的逆元。
当然这里求出来的逆元是在取模p的逆元,对我们最终目标没有影响。这也是比较方便而且比较好的方法。
HDU 3939 3944 3037








 Problem Description
Problem Description
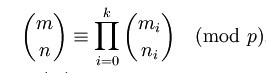

















 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








