斜率优化dp总结（AcWing任务安排123题解）

感想

前两天在$Acwing$学的斜率优化$dp$，当天是学的差点自闭，今天正好有空就抽点时间出来总结一下。任务安排$123$是$acwing$中用来讲解斜率优化$dp$时候用到的三道例题，其中$1$的数据比较弱，可以直接用普通$dp$做出来，$2$就是标准的斜率优化$dp$的板子，把$1$的结论直接套板子就能写了，$3$是在$2$的基础上再一次加强了自己数据，需要用到二分优化。斜率优化$dp$的优化方式还是比较多的，平衡树，$CDQ$等等，这些就等以后学了再慢慢总结吧。

题意

有$N$个任务要到一台机器上去做，机器每次开启都要花费$S$的时间，每个任务都要花费$T_i$的时间，每个任务有$C_i$的重要度。但每次任务完成后都不会直接计算花费，而是要等到机器下一次停了之后再进行结算，结算方式为$t_{当前}\ast c_{任务}$的总和。现在这台机器可以关闭启动无限多次，请问花费最小是多少？

题解

任务安排$1$

任务安排$1$数据范围

先列出$dp$数组$dp[i]$代表如果在$i$任务结束后暂停机器花费最小是多少。列出转移方程：
dp[i]=min{dp[j]+sTi∗(sCi−sCj)+S∗(sCn−sCj)} dp[i]=min\{dp[j]+sT_i*(sC_i-sC_j)+S*(sC_n-sC_j)\} dp[i]=min{dp[j]+sTi​∗(sCi​−sCj​)+S∗(sCn​−sCj​)}
$sT$和$sC$分别代表$T$和$C$的前缀和。其中$S\ast (s{C}_n-s{C}_j)$代表当前这次机器开启会造成接下来的任务增加的花费，$s{T}_i\ast (s{C}_i-s{C}_j)$代表在不考虑机器开启导致的花费增加的情况下本次开启机器造成的任务花费。

这里我们用到了费用提前计算的思想，也就是$S\ast (s{C}_n-s{C}_j)$。我们可以这样理解如果我们在$j$发生之后重新启动机器，之后的任务的结束时间都要往后顺延$S$的单位时间，费用都要增加$S\ast (s{C}_n-s{C}_j)$，如果我们采用了这个策略，无论后面怎么选，这些增加的费用都是逃不掉的，与此同时如果我们在后面还想要也就是由$dp[i]$转移出去的时候我们还想要计算这个值并不方便，所以我们就可以选择在此之前提前计算掉。

void MAIN(){
    memset(dp,0x3f,sizeof(dp));
    cin>>n>>s;
    for(int i=1,t,c;i<=n,cin>>t>>c;i++) st[i]=st[i-1]+t,sc[i]=sc[i-1]+c;
    dp[0]=0;
    for(int i=1;i<=n;i++){
        for(int j=0;j<i;j++){
            dp[i]=min(dp[i],dp[j]+(sc[i]-sc[j])*st[i]+s*(sc[n]-sc[j]));
        }
    }
    cout<<dp[n]<<endl;
    return ;
}

至此，$1$的题解完毕。

任务安排$2$

$2$与$1$最大的不同在于数据范围的扩大。

任务安排$2$数据范围

很明显我们上面用的$O(n^2)$的算法已经不能用了，我们应该研究更加高效的算法。
dp[i]=min{dp[j]+sTi∗(sCi−sCj)+S∗(sCn−sCj)} dp[i]=min\{dp[j]+sT_i*(sC_i-sC_j)+S*(sC_n-sC_j)\} dp[i]=min{dp[j]+sTi​∗(sCi​−sCj​)+S∗(sCn​−sCj​)}
首先我们来简化一下上面的公式。

我们已经枚举到了$i$，换句话说$i$是已经确定的值，而哪一个$j$代价最小是未知的，是我们要求的值。

那我们把已经确定了的值认为是常量提出来。
dp[i]−S∗sCn−sTi∗sCi=min{dp[j]−(sTi+S)∗sCj} dp[i]-S*sC_n-sT_i*sC_i=min\{dp[j]-(sT_i+S)*sC_j\} dp[i]−S∗sCn​−sTi​∗sCi​=min{dp[j]−(sTi​+S)∗sCj​}
等式左边的是我们要求的对象我们将他们设为常量$b$，右边设为未知量$x=s{C}_j,y=dp[j]$，$s{T}_i+S$是一个常量我们设为$k$，得出
$$\{\begin{array}{l}x=s{C}_j\\ y=dp[j]\\ k=s{T}_i+S\\ b=dp[i]-S\ast s{C}_n-s{T}_i\ast s{C}_i\end{array}$$
我们就将上述的等式转换成了$b=y-kx$我们要求最小值也就变成了求$b_{min}$，换句话说我们要找到一个点（这个点就是我们之前遍历过的所有$dp$数组中的一个），使得这个$b$最小。

那么现在我们的任务就变成了如何在可以接受的时间复杂度范围内找到这个点。

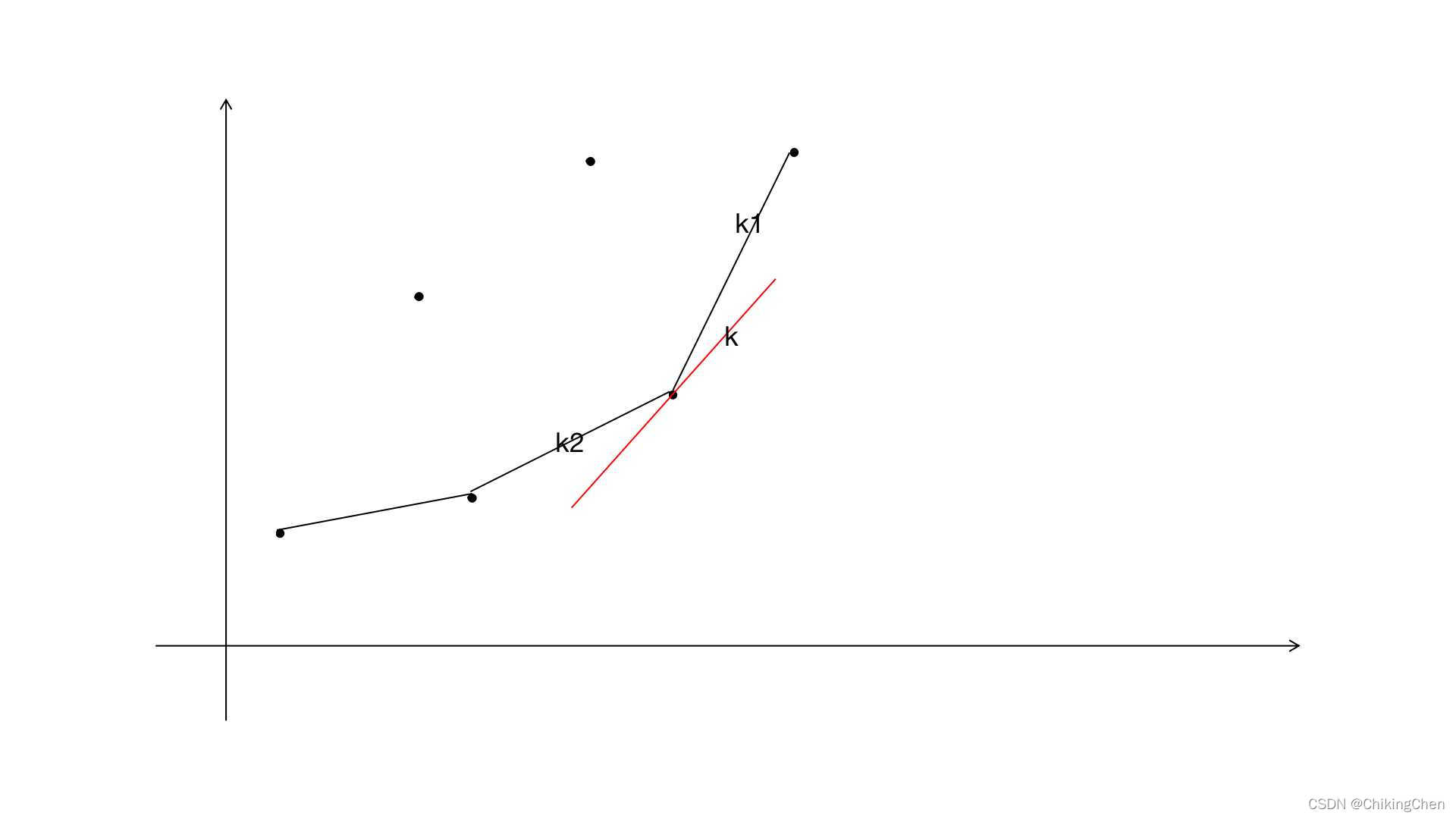
如图所示是我们当前情况下能够找到的$b$最小的点，这个点显然是在凸包上面的并且满足$k1<k<k2$，其中$k1,k2$分别代表当前点与相邻点的斜率，同时凸包上相邻的点斜率递增。

再回到我们上面列出的方程
$$\{\begin{array}{l}x=s{C}_j\\ y=dp[j]\\ k=s{T}_i+S\\ b=dp[i]-S\ast s{C}_n-s{T}_i\ast s{C}_i\end{array}$$
我们能够发现$k(i)$带有明显的单调性，同时凸包的斜率也有单调性。

这边我们想到用单调队列来维护凸包的单调性。因为考虑到$k(i)$单调递增之前小于$k(i-1)$的斜率绝对不会大于$k(i)$，所以我们可以直接将他们弹出队列，最后剩下的头节点就是被转移的对象。与此同时为了维护凸包的单调递增，我们在将新的节点加入单调队列的同时也要检查新加入的节点与尾节点以及尾节点与尾节点前一位的节点的斜率的单调性。

这里可能有点绕，因为一个对象他表现了两种性质，在找被转移对象时候我们用到的是他的$k$值，而在加入单调队列时候我们用到的是他的坐标值$(x,y)$。

最后放一个$OIwiki$上的总结：

1. 将初始状态入队
2. 每次使用一条和$i$相关的直线$f_i$去切维护的凸包，找到最优决策，更新$d{p}_i$
3. 加入状态$d{p}_i$。如果一个状态（即凸包上的一个点）在$d{p}_i$加入后不再是凸包上的点，需要在$d{p}_i$加入之前剔除

void MAIN(){
    cin>>n>>s;
    for(int i=1,c,t;i<=n,cin>>t>>c;i++) sc[i]=sc[i-1]+c,st[i]=st[i-1]+t;
    int head=0,tail=0;
    for(int i=1;i<=n;i++){
        int k=st[i]+s;
        while(head<tail&&k*(x(dq[head])-x(dq[head+1]))<=y(dq[head])-y(dq[head+1])) head++;
        int j=dq[head];
        f[i]=f[j]+st[i]*(sc[i]-sc[j])+s*(sc[n]-sc[j]);
        while(head<tail&&(y(dq[tail])-y(i))*(x(dq[tail])-x(dq[tail-1])) > (y(dq[tail])-y(dq[tail-1]))*(x(dq[tail])-x(i))) tail--;
        dq[++tail]=i;
    }
    cout<<f[n]<<endl;
    return ;
}

任务安排$3$

$3$的数据范围

我们直接把上面的代换放下来
$$\{\begin{array}{l}x=s{C}_j\\ y=dp[j]\\ k=s{T}_i+S\\ b=dp[i]-S\ast s{C}_n-s{T}_i\ast s{C}_i\end{array}$$
可以看到新的数据中$k$已经失去了单调性，上面单调队列的做法已经不可取。

但不变的是凸包斜率的单调性没有变化，我们可以将点存放在队列中，并直接在队列中二分找到目标点位然后算出答案。

然后再根据单调性来维护队列的单调性加入点位。

bool check(int x){
    if((x(que[x+1])-x(que[x]))*k<(y(que[x+1])-y(que[x]))) return true;
    return false;
}
int binary_search(int l,int r){
    if(l==r) return l;
    int mid=(l+r)>>1;
    if(check(mid)) return binary_search(l,mid);
    else return binary_search(mid+1,r);
}
int read() {
    int x=0,f=1;
    char c=getchar();
    while(c<'0'||c>'9'){if(c=='-') f=-1;c=getchar();}
    while(c>='0'&&c<='9') x=x*10+c-'0',c=getchar();
    return x*f;
}
void write(int x) {
    if(x<0) putchar('-'),x=-x;
    if(x>9) write(x/10);
    putchar(x%10+'0');
}
void MAIN(){
    n=read();s=read();
    for(int i=1;i<=n;i++) st[i]=read(),sc[i]=read();
    for(int i=1;i<=n;i++) st[i]+=st[i-1],sc[i]+=sc[i-1];
    int border=0;
    for(int i=1;i<=n;i++){
        k=st[i]+s;
        int x=binary_search(0,border);
        f[i]=f[que[x]]+st[i]*(sc[i]-sc[que[x]])+s*(sc[n]-sc[que[x]]);
        while(border!=0&&(y(i)-y(que[border]))*(x(que[border])-x(que[border-1]))<=(y(que[border])-y(que[border-1]))*(x(i)-x(que[border]))) border--;
        que[++border]=i;
    }
    write(f[n]);
    return ;
}

结语

到现在为止我已经讲完了斜率优化$dp$及其二分优化，当然二分优化之外还有平衡树优化等等，不过考虑到我太菜以及我手上没有配套的题目还是有空再说吧。