快速幂问题

前言

	简单问题,写的不好,大佬见谅.
	如有疏漏,欢迎指正,小编垂首.

问题描述:

快速幂：指数 x的y次方。不能使用 power()函数;
X^y(直接使用for循环),但当y很大时怎么办?
例:y=10^18
有一个求解快速幂的好办法,公式如下

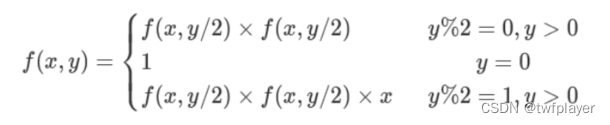
来试试吧!

问题解析:

使用题目中的算法求解:
该算法又叫反复平方法,如题:
如果y可以写成2^n,那么
下x^y = ((x²)²)²…
时间复杂度从O(n)下降至㏒()

实现代码:

代码如下（示例一）：为了递归而递归

#include<iostream>
using namespace std;

long long power(int x, long int y) {
	if (y == 0) return 1;
	if (y > 0) {
		long long t = power(x, y / 2);
		if (y % 2 == 0) {
			return t * t;
		}
		if (y % 2 == 1) {
			return t * t * x;
		}
	}
	return -1;
}

long long result(int x,long int y,int p) {
	return power(x, y) % p;
}

int main() {
	int t,x,p;
	long int y;
	cin >> t;
	getchar();//吸收缓冲区字符
	while (t > 0) {
		cin >> x >> y >> p;
		cout << result(x, y, p) << endl;
		t--;
	}
	return 0;
}

代码如下（示例二）推荐使用：

#include<iostream>
using namespace std;

long long power(int x, long int y) {
	long long res = 1;
	while (y) {
		if (y & 1) {
			res *= x;
		}
		x *= x;
		y >>= 1;
	}
	return res;
}

long long result(int x,long int y, int p) {
	return power(x, y) % p;
}

int main() {
	int t, x, p;
	long int y;
	cin >> t;
	getchar();//吸收缓冲区字符
	while (t > 0) {
		cin >> x >> y >> p;
		cout << result(x, y, p) << endl;
		t--;
	}
	return 0;
}

测试案例:

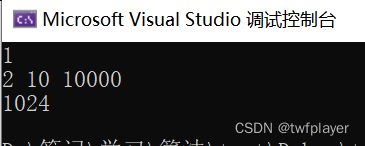
注意事项

算法示例一:只是为了练习递归啦
算法示例二:显然位运算比较快啦

总结

快速幂
不能使用power函数,那就自己写一遍呗.