基于OpenCV的图像编解码实践

原图：

图像信息,可以看到图像是一个816*2100像素的图片:

python代码：

import cv2
import numpy as np
import matplotlib.pyplot as plt
 
img = cv2.imread('11.jpg', 0)
img1 = img.astype('float')
img_dct = cv2.dct(img1)
img_dct_log = np.log(abs(img_dct))
img_recor = cv2.idct(img_dct)
recor_temp = img_dct[0:100,0:100]
recor_temp2 = np.zeros(img.shape)
recor_temp2[0:100,0:100] = recor_temp
print recor_temp.shape
print recor_temp2.shape
img_recor1 = cv2.idct(recor_temp2)
plt.subplot(221)
plt.imshow(img)
plt.title('original')
plt.subplot(222)
plt.imshow(img_dct_log)
plt.title('dct transformed')
plt.subplot(223)
plt.imshow(img_recor)
plt.title('idct transformed')
plt.subplot(224)
plt.imshow(img_recor1)
plt.title('idct transformed2')
 
plt.show()

仅仅提取一个100*100的DCT系数后的效果：

x

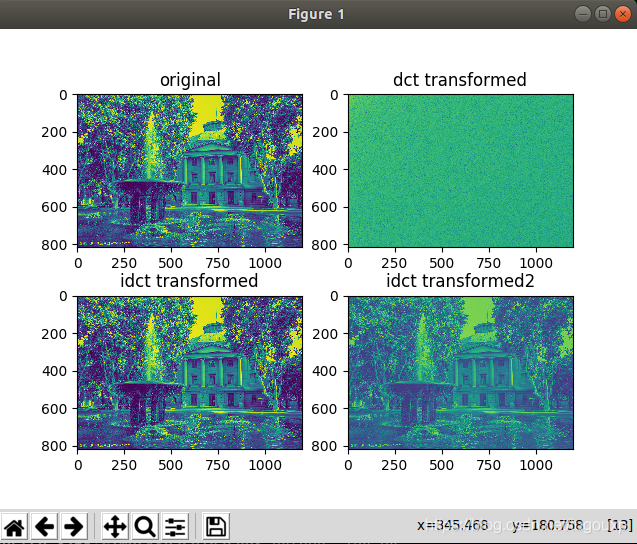
当用800*1000的DCT系数：

可以看到图像细节更丰富了一些：

import cv2
import numpy as np
import matplotlib.pyplot as plt
 
img = cv2.imread('11.jpg', 0)
img1 = img.astype('float')
img_dct = cv2.dct(img1)
img_dct_log = np.log(abs(img_dct))
img_recor = cv2.idct(img_dct)
recor_temp = img_dct[0:800,0:1000]
recor_temp2 = np.zeros(img.shape)
recor_temp2[0:800,0:1000] = recor_temp
print recor_temp.shape
print recor_temp2.shape
img_recor1 = cv2.idct(recor_temp2)
plt.subplot(221)
plt.imshow(img)
plt.title('original')
plt.subplot(222)
plt.imshow(img_dct_log)
plt.title('dct transformed')
plt.subplot(223)
plt.imshow(img_recor)
plt.title('idct transformed')
plt.subplot(224)
plt.imshow(img_recor1)
plt.title('idct transformed2')
 
plt.show()

当用816*1200的DCT系数：

可以看出图像恢复到原来的质量了．

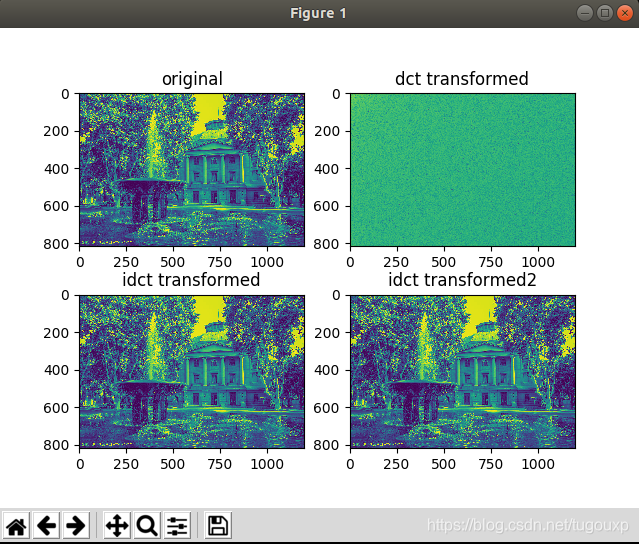
去掉低频分量，保留高频分量系数，看一下DCT反变换后图片的效果，下面的例子中将左上角30*30的DCT系数设置为０．

import cv2
import numpy as np
import matplotlib.pyplot as plt
 
img = cv2.imread('11.jpg', 0)
img1 = img.astype('float')
img_dct = cv2.dct(img1)
img_dct_log = np.log(abs(img_dct))
print abs(img_dct)
print "------------------------------------------------------------------"
print img_dct_log
img_recor = cv2.idct(img_dct)
recor_temp = img_dct[0:816,0:1200]
recor_temp2 = np.zeros(img.shape)
recor_temp2[0:816,0:1200] = recor_temp
print recor_temp.shape
print recor_temp2.shape

for i in range(30):
    for j in range(30):
        recor_temp2[i][j]=0;

img_recor1 = cv2.idct(recor_temp2)
plt.subplot(221)
plt.imshow(img)
plt.title('original')
plt.subplot(222)
plt.imshow(img_dct_log)
plt.title('dct transformed')
plt.subplot(223)
plt.imshow(img_recor)
plt.title('idct transformed')
plt.subplot(224)
plt.imshow(img_recor1)
plt.title('idct transformed2')
plt.show()

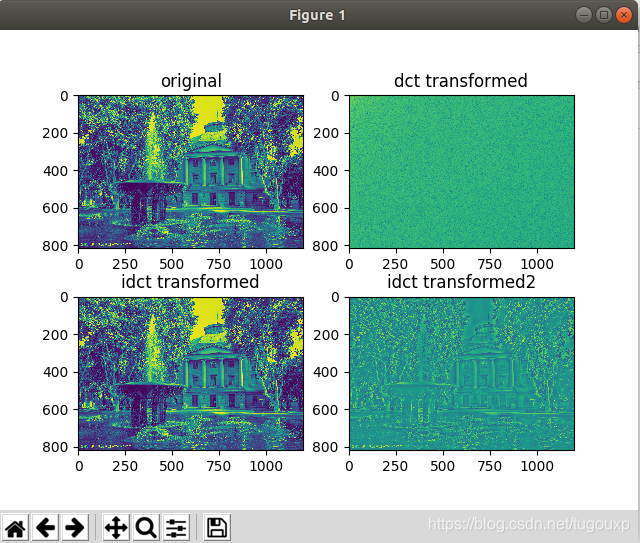
可以看到，图片中只剩下了变化剧烈的高频信号区域．怎么类比这件事情呢，图片是二维的，不好类比，我们就拿一维的信号为例，典型的一维信号就是数字电路时钟，时钟信号常常是电路系统中频率最高和边沿最陡的信号，多数EMI问题的产生和时钟信号有关，其实我们见过的经典傅里叶分析的例子方波信号就和时钟信号很相似，如下图的方波密度谱，它的陡峭边沿产生了大量的高频信号分量，对应于我们这里高频分量的IDCT变换能够反应图片的高频轮廓部分。如果我们选择它作为IDCT反变换的系数，能够得到对变化剧烈部分的描述。也就是图片轮廓。

---

分析代码：

img_dct保存的是dct变换后的矩阵，img_dct_log是矩阵中的元素首先取绝对值，再求对数的矩阵．

img_dct_log = np.log(abs(img_dct))

那么对数的底是多少呢？

打印出来img_dct_log和abs(img_dct)看一下：

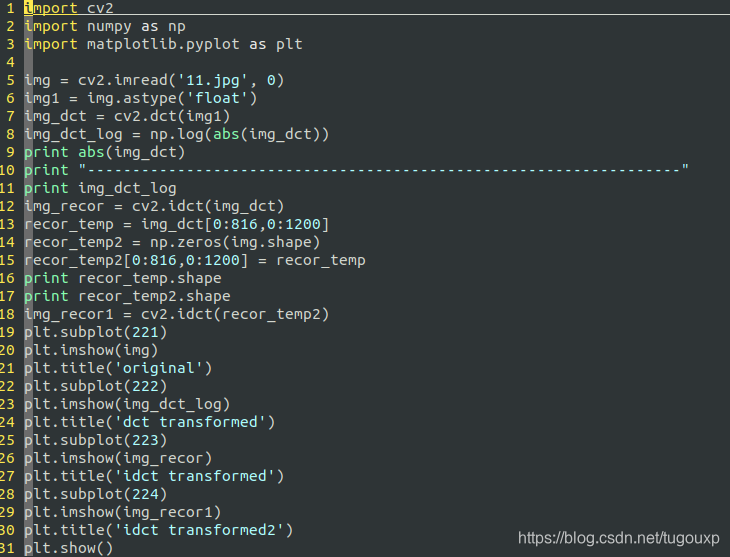
打印结果：

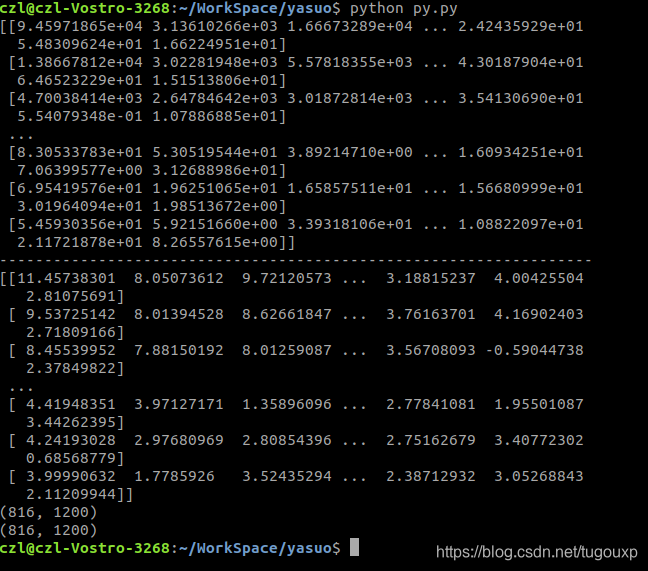
其中9.45971865e+04=9.45971865 x 10^4 =94597.1865表示的是科学计数法．

  

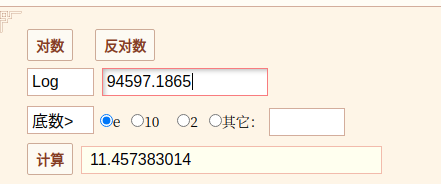
我们看到只有在底数取e的时候，对应的对数才符合题目输出要求，所以,python numpy.log函数取的是以自然常数e为地的对数．

---

这个试验让我联想到一个问题，实验中我们都是按照图的大小进行DCT变换的，相当于整张图作为一个宏块儿，而真正应用场景中的VPU编码，宏块大小都是有限制的，一般是8*8或者16*16个像素方阵大小，直接把一张图片看成一个宏块，还能节省掉方块滤波这个环节，为什么实际中不用呢？

经过请教高人,得到了答案，现在总结如下：

算法限制：视频编码属于有损编码，其本质是去除冗余信息。去除冗余信息的基本手段是差值编码，简单可以理解为记录一个或几个像素作为参考值，其它像素与它或它们相减，记录之间的差值（这让我联想到了GIT版本管理的原理），而这些参考像素的选取有多种模式（帧内预测、帧间预测）。如果整一帧都选取少数几个参考值，那肯定做不到最优解的。所以必须分块来做。DCT变换成频域，只是为了方便量化（滤除部分高频纹理信息）。DCT变换的最终表现形式是H*A*H^T（变换矩阵*输入像素矩阵*变换矩阵的转置矩阵），这里的三个矩阵都是方阵。从这里可以看出DCT变换有两个问题：（1）维数越高，计算复杂度越大；（2）不能适应非方形的图片。另外一个DCT变换只能使用一个量化参数，不能做区域差异，不利于基于人眼感知的区域图像压缩。

硬件限制：硬件处理数据时，是要靠SRAM缓存的，SRAM越大越多，芯片面积也越大。所以硬件读入数据都是以固定的MB size为单位，每个处理模块都使用固定的SRAM。如果给你开一个4K的SRAM，你觉得面积得有多夸张。

关于宏块大小定义，H265标准规定分块为64*64~4*4，公司做H265时，做了裁剪，最大只支持到32*32。所以编码器的MB也是按32*32为基准。中间为了做边界滤波等特殊操作，某些模块会加大一点。

关于对齐:为啥一些模块的输入或输出数据的DRAM buffer申请，宽高必须要多少对齐：硬件的每一个操作是有一定周期的，这里的周期可以看成2的幂数倍个晶振输出的脉冲信号。而为了压榨在固定周期内的使用效率，并且兼顾H265等标准，在读取数据时，会以N个32*32块为单位读数的。所以有时候，如果图像的宽高不能整除这个读数单位块的宽高，就会出现读数超过实际图像边界的情况。而为了避免出现硬件扫描到未malloc的DRAM地址，就必须申请大于实际图像size的DRAM buffer。其实如果没有使用IOMMU的话，硬件扫描buffer越界，也只是会超出一点点，只要没有刚好跟别的地址有重叠，一般不会有什么问题。就是上了IOMMU，对buffer管理严格了，才会出各种对齐问题。

视觉领域的女神图

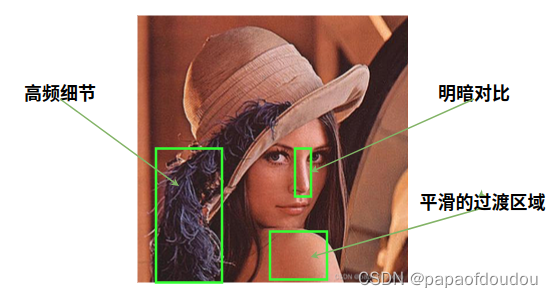
数字信号处理中的行业中经常使用下面这张图作为标准输入验证编码算法的性能，这是为什么呢?

首先，它不但有丰富的细节，还有鲜明的明暗对比和平话的过渡区域，这就可以充分考验压缩算法的能力，图像是由无数个像素组成的，像素会转化为数字信号，细节丰富的区域会转化成高频信号，比较难处理，过渡平滑的区域对应低频信号，比较好处理，厉害的算法要兼顾高频信号和低频信号，lena这张照片等于给算法除了一张题目完整覆盖了考点，又兼顾了普通题和难题的考卷，可以完整测试算法的能力，其次，我们人类对人脸的辨识能力比较强，猫猫狗狗图片压缩后的变化可能看不出来，但是人脸上细微的改变我们可以识别出。最后一个原因，看过lena全身照的都会明白的。

总结：

压缩编码这也就是一个很自然的思路, 把无关的高频细节给去掉，从而获取性能上的好处！网络图像压缩技术不就是这么整的么！PCA主成分、傅立叶分解的思路不都是这样的么！抓住事物的主要矛盾，忽略细节，从而提高整体性能！就像机器学习里的正则化优化不也是这样么，避免你过于钻到细节里面从而产生过拟合啊！这么一想，其实，我们人生不也是这样么？什么事情都得抠死理，钻牛角尖么？！！有时候主动放弃一些东西首先你的人生肯定会轻松很多，其次说不定会收获到更稳定的人生幸福值（泛化性能）呢

---

结束！