战斗机做机动动作的时候经常会执行偏航,俯仰和翻滚等动作,用来改变飞机的运行轨迹,这里面也蕴含了丰富的线性空间变换的思想和应用。本篇文章试图用线性代数的理论来解释这些操作具体是怎么做的,当然,同样的解释也可以用在机器人,机械手臂的运动上面。
方便起见,将坐标系选在飞机上,假定飞机处于平面,机头指向
轴的正方向,左机翼指向
轴的正向,飞机在
平面飞行,
轴定义在飞行平面的法线方向,机头上面为正。如下图所示:

当飞机飞行时,三个坐标轴和飞机同时运动。
我们分别讲述:
1.偏航
偏航是一个在平面的旋转,以偏航45°为例,此时,飞机右转45°(顺时针方向),从三维线性变换的角度看,偏航就是关于
轴的旋转,如果飞机机头的初始坐标表示为向量
,则偏航后,它的坐标仍然是
,这是因为坐标轴连同飞机一起旋转,暂且把变换前的坐标系统成为初始坐标系统,偏航45°后,机头相对于初始坐标系统的位置为:

如果将偏航变换L堪称初始坐标系统的变换,则容易求得它的表示矩阵,如果L对那个的偏航角度为,则L将(1,0,0)和(0,1,0)分别旋转为点
和
点在偏航时将保持不变,因为它在旋转轴上。对列向量,若
为L在
中的坐标向量,则
则,偏航的变换矩阵为:
2.俯仰
飞机的俯仰是在平面的旋转,当角度为负时,机头向下旋转,反之,则向上。从三维空间线性变换的角度看,俯仰就是关于
轴的旋转,正如偏航一样,也存在一个相对于初始坐标系的转移矩阵。若L是一个旋转角度为
的俯仰变换,则L表示的矩阵为:
3.翻滚
飞机的翻滚是在平面的旋转,左翼向上,右翼向下,旋转为正方向。从三维空间线性变换的角度看,翻滚就是关于
轴的旋转,类似于偏航和俯仰,可以i球的翻滚变换关于初始坐标系的转移矩阵。
如果先偏航角度,然后俯仰角度
,这个复合变换是线性的,它的变换矩阵并不是乘积
,偏航的作用是将标准基向量
转换到新的方向
,所以向量
将用于定义俯仰时新的
轴的方向,接下来的俯仰变换是针对新的
轴进行的(即向量
指示的方向),向量
构成一个平面,而且在俯仰时,它们将在平面内一起旋转角度
,向量
在俯仰时不受影响,因为它在旋转轴上。因此,符合变换L对于标准基向量的作用为:
标准基向量的象构成符合变换表示矩阵的列向量。
所以,符合变换的表示矩阵是分别表示偏航和俯仰的两个矩阵的成乘积,但乘积必须以相反的顺序进行 ,即偏航矩阵在左,俯仰矩阵
在右,类似的,偏航角度
,然后俯仰角度
,再翻滚角度
的符合变换表示矩阵应为乘积
可以这样理解,假设依次经过偏航,俯仰,翻滚三次变换后,新坐标系中的向量
则在翻滚变换前,向量为
俯仰变换前,向量为
偏航变换前,向量为
所以
其中是变换前坐标系衡量的坐标,
则是新坐标系下的坐标
标准坐标系下的向量等于
坐标系下的
向量,可以写成:
类似于C语言编程中的变量定义.
int a;
double abc;
遵从“类型+对象”的形式,这里矩阵即使类型,对象即是向量坐标.
想到另外一种复合变换的理解方式:
假设初始坐标系为标准坐标系,保持不变,则变换是在
基的基础上进行的变换,所以,相对于原坐标系来说,假设坐标向量为
,变换后在原坐标系下的新坐标为
,变换算子为
。
变换后在原坐标系下坐标变为,变换算子为
所以,综合进行Y,R变换后,原向量经过变换后在原来坐标系中的新坐标为变换算子相乘:
先进行Y变换,在进行R变换得到:
同样道理,将看成一个变换,在它的基础上再进行
变换,则R变换是在
基上进行的,同样道理,在原坐标系中,
变换算子应该是
所以,依次进行Y,P,R变换得到的复合变换应该是复合直观上的三次变换矩阵的乘法:
其中,
,
分别是从原坐标系角度,看到的
变换的变换矩阵,这样就符合右乘的直观理解了,过程如下图所示:
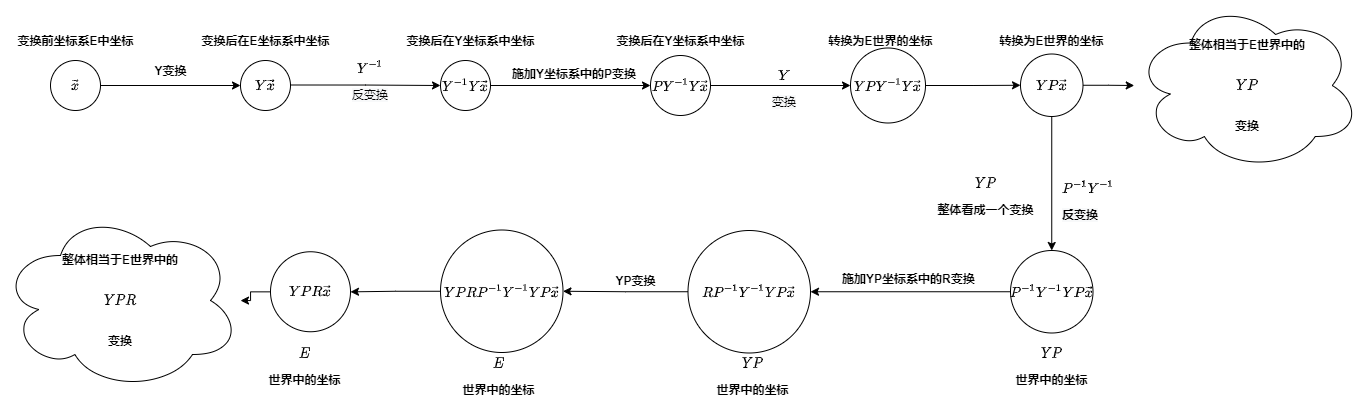
如下图所示:
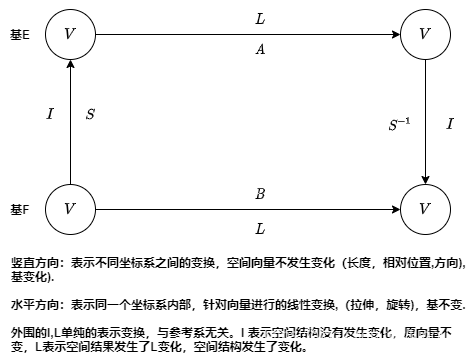
这里一定刚要区分空间变换和视角变换:
视角变换:观察角度的变化,控件本身并未发生改变,矩形还是原来的矩形,正方形还是原来的正方形,空间结构没有发生变化。
空间变换:空间本身发生改变,空间被扭曲,拉伸等等,比如,矩形变成了平行四边形等等。这里要注意一种特殊的空间变换,就是正规矩阵引起的正交变换,正交变换不会扭曲,变形任何东西,但是它属于空间变换。
当然,这里可能需要假设,空间是存在绝对方位的,也就是存在真正的单位矩阵., 从这个角度上说,视角变换可以看成一种特殊的空间变换。
实际上,线性代数高级教程中(非误人子弟的同济版)有一条定理,描述如下:
令
以及
为一个向量空间的两个有序基,并令
为
上的线性算子,令
为从
到
的转移表示矩阵,若
为
相应于
的表示矩阵,且
为
相应于
的表示矩阵,则
,或者
这条定理的证明也很简单:
把看成恒等变换
相应于有序基
和
的表示矩阵,那么:
为
相应于
和
的表示矩阵:因为对于
中向量
施加恒等变换
(也就是保持不变),相当与
中的坐标
为
相应于
的表示矩阵:所以
为
相应于
和
的表示矩阵:因为对于
中向量施加恒等变换
(也就是保持不变),相当与
中的坐标左乘
,也就是
所以,相当于F中向量,经过A变换后,得到F中的坐标
, 所以,同一个变换,在E和F中的表示是不同的,但是它们具有相似关系。
将上面的定理映射到在变换后俯仰的问题:
俯仰
角度
初始坐标系
变换后的新坐标系
相对于新坐标系
的变换,这里就是P
P变换相对于
的表示矩阵.
相对于新坐标系F的变换,这里就是
套用上述公式,可以得到:
例:
假设


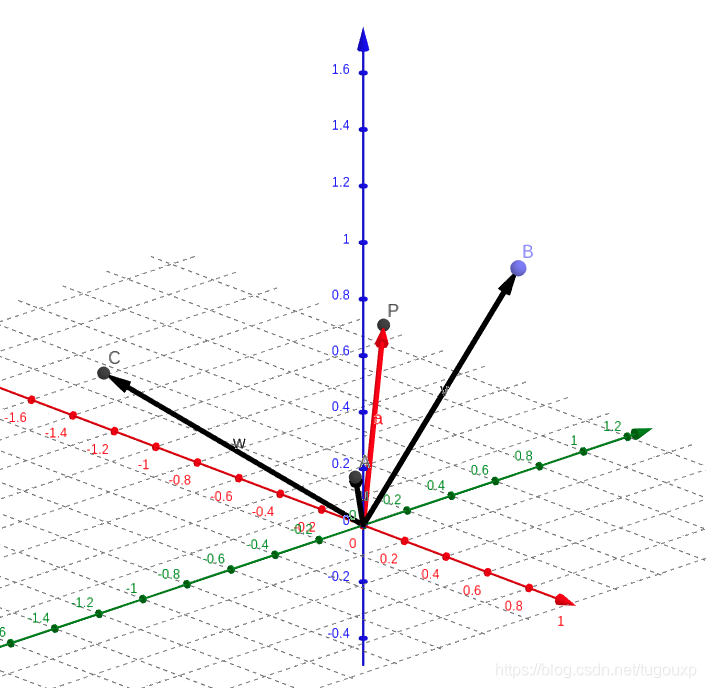
根据octave计算出来的特征值和特征向量,可以看出,两个复特征值互为共厄,对应的特征向量也是互为共厄的关系,组合向量有一个特征值为1,并且对应的特征向量是实向量,实际上,三维空间中的正交变换必定存在特征值为1的特征值(刚体变换,不改变刚体任何方向上的长度),这个特征值和特征向量有非常深刻的意义,它可以将上面的三种变换归为一种变换,特征向量对应的方向即是新变换的对称轴,我们后面在说.关于条的证明,请参考我的博文线性空间一些基本性质的证明30.(基本结论是:在三维空间中的刚体变换,一定存在一个对称轴,在对称轴方向上,刚体的尺度不发生变化(特征值为1))
下图中是对称轴,
分别是原来的
轴变换后的样子,注意整个变换相当于坐标系沿着
做了一次旋转.
关于这种围绕特征向量方向做对称旋转的关系,可以由下图进行直观的说明.
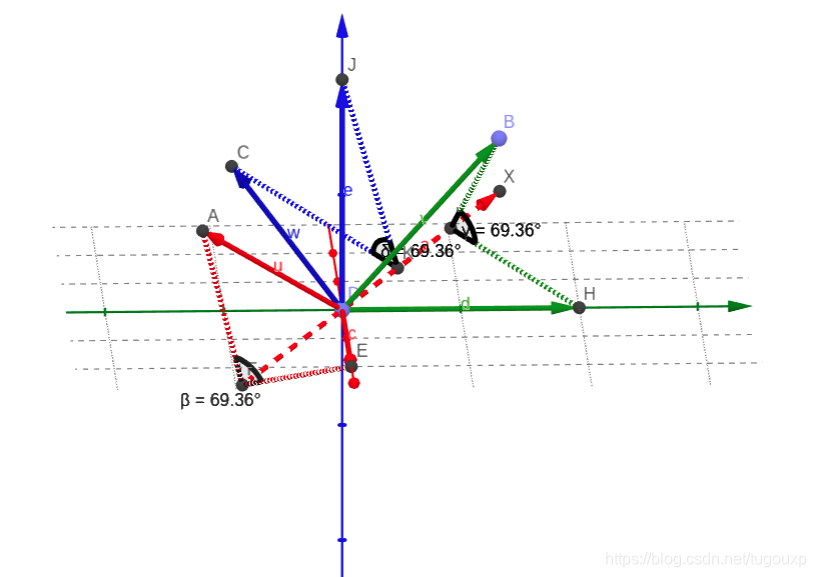
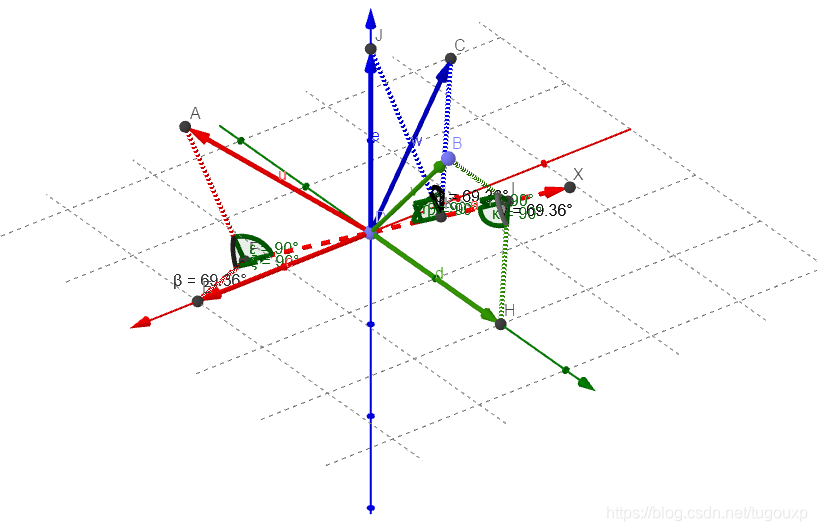
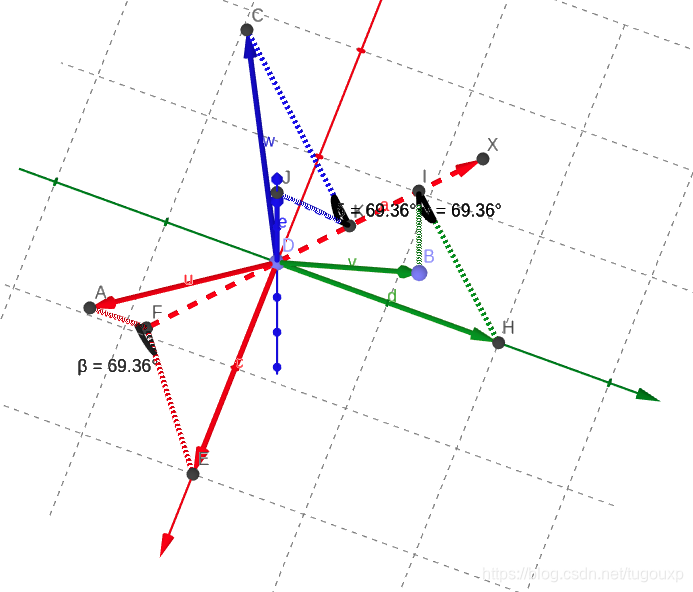
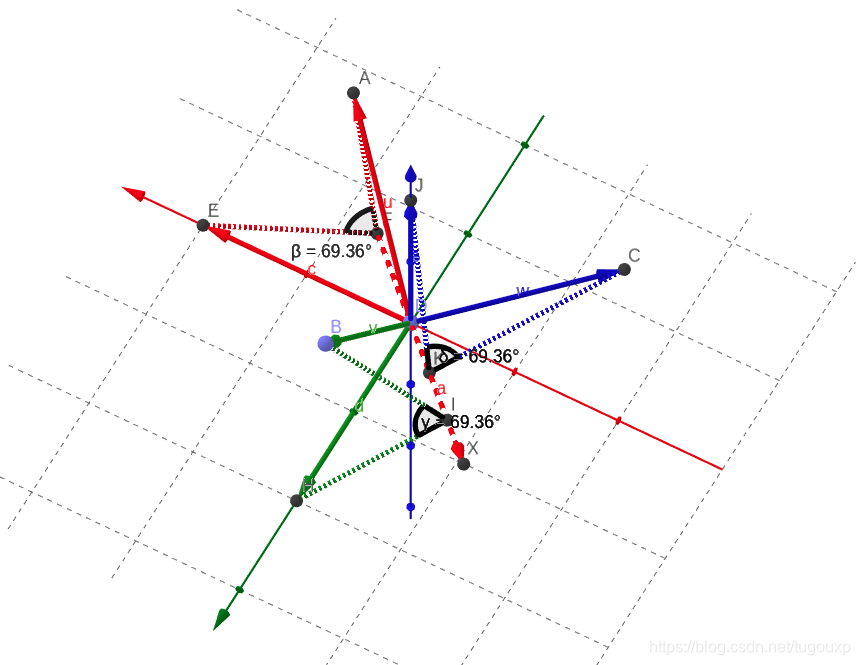
来一张轴的特写:
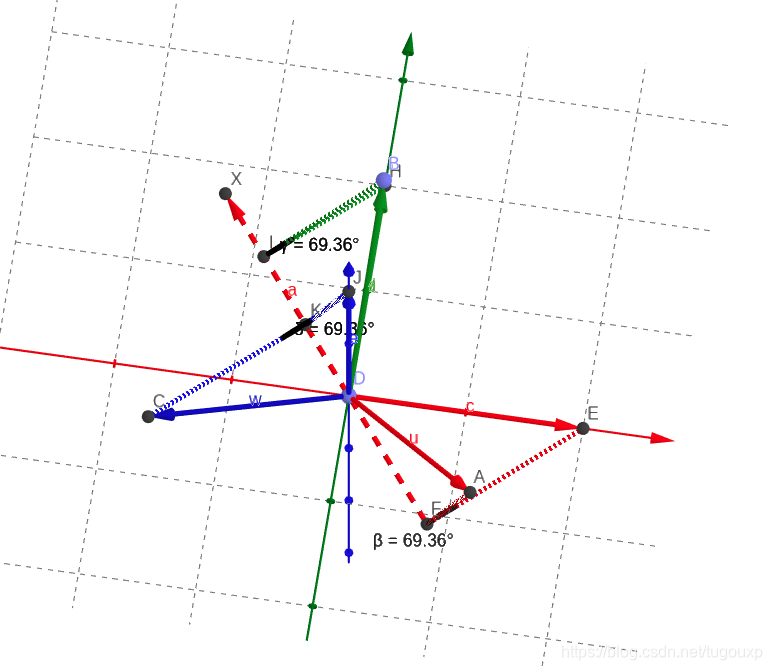
综上所述,偏航
俯仰
翻滚
的综合效果,相当将坐标系围绕单位特征向量
旋转69.36°变换一次完成的效果,所以战机没必要按部就班的一个一个的做动作了,只要按照计算得到的向量方向做一次69.36°的旋转,即可一步到位,这里特征向量指向的方向就是对称轴,这就是特征向量在工程中的物理意义。








 本文通过分析战斗机的偏航、俯仰和翻滚动作,探讨了线性变换在飞机姿态控制中的应用,利用线性代数理论解释了这些操作如何改变飞机的运行轨迹。同时,这一理论也可应用于机器人和机械臂的运动控制。文中详细阐述了各个动作的线性变换矩阵,并讨论了复合变换的理解方式,强调了特征向量在工程中的物理意义。
本文通过分析战斗机的偏航、俯仰和翻滚动作,探讨了线性变换在飞机姿态控制中的应用,利用线性代数理论解释了这些操作如何改变飞机的运行轨迹。同时,这一理论也可应用于机器人和机械臂的运动控制。文中详细阐述了各个动作的线性变换矩阵,并讨论了复合变换的理解方式,强调了特征向量在工程中的物理意义。

















 894
894

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










