关于特征值和特征向量的直观意义

大部分工科专业在学习现行代数会使用同济大学的教材，这本教材在传授过程中，全程给人一种莫名奇妙的感觉，从头到尾都在爱灌输一些莫名其妙的计算规则，所以，你可能在期末考试中考了高分，但仍然不明白现性代数的概念到底在实际中意味着什么，直到工作后，当看到一些四层相似的规则在某个领域中应用的时候，你才会大呼相见恨晚，恨不得从头把线性代数在从头学一变．

对于具有n个不同特征值的线性变换矩阵A来说

设其特征值以及对应的特征向量分别为：

         

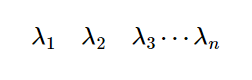
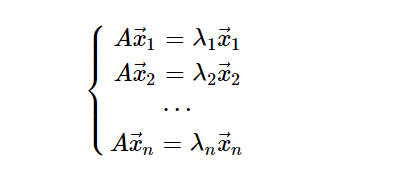
转换一下形式：

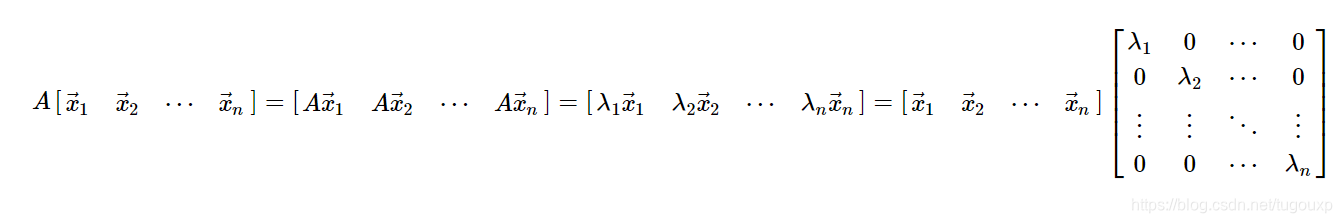
令P,V分别等于

则上式等价 于:

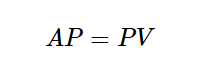
两边左乘以V的逆，

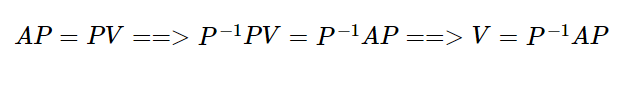
V是特征值为对角的对角矩阵，而P是由特征向量为列组成的方阵。V为A的相似矩阵，表征同一个线性变换，只是观察的角度有差异。

现在我们可以建立两个世界坐标，第一个坐标是标准的坐标系：

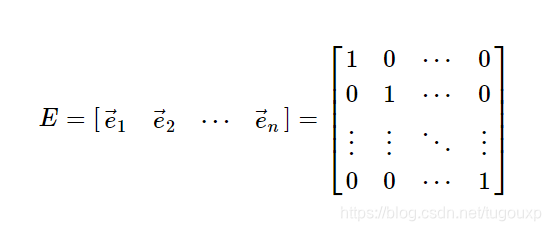
第二个坐标系是由矩阵的特征向量组成的坐标系P：

       

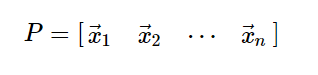
我们尝试分析一下，如果不断的施加线性变换A，同一个向量在如上两个坐标系中描述的坐标各是什么样子

设在P世界中的坐标为

    

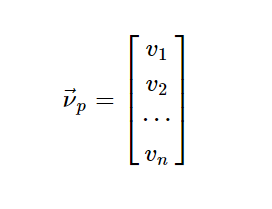
由于线性变换是用E世界的矩阵A描述的，所以，如果需要对向量v施加A变换，必须将其首先转化为 E世界的坐标系坐标

 根据转换关系：

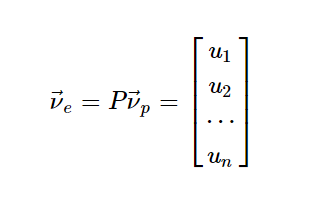
对v(p)进行一次A变换，相当于对v(e)进行A变换，在转换为P世界的坐标，则

反向推导：

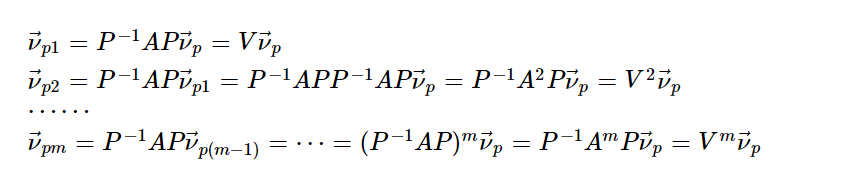
正向推导：

　

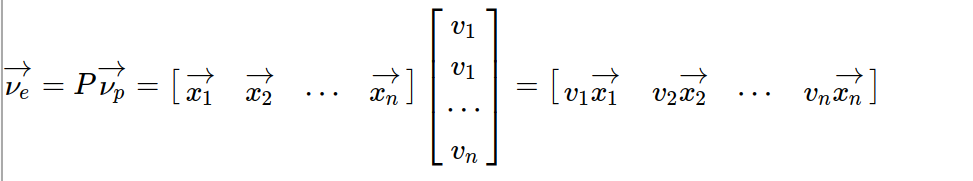
所以：

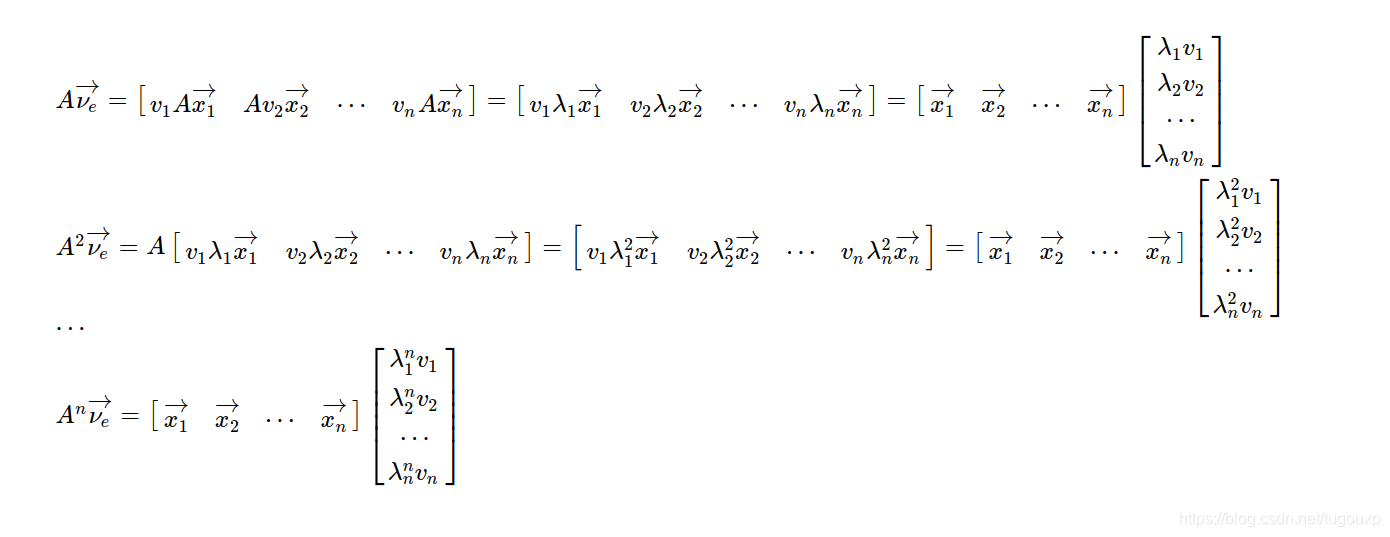
也就是经过m次的A变换后，E世界中的坐标已经面目全非，看不出任何规律，但是从P世界的角度看，向量的变换出奇的有规律，变换后的坐标全部是

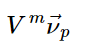
的形式：

也就是

也就是经过m此A变换后，以P世界坐标轴描述的坐标沿每个坐标轴方向，长度伸长了对应特征值的

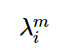
倍，其中i是对应P世界的某个坐标轴

所以，很明显，同一个线性变换，在E世界用很复杂的A来描述，但是在P世界，只要对角阵矩阵V即可描述。变换的特征一眼就能看出来。

以矩阵为例，

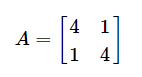
它的特征向量和特征值为：

特征向量是图中红色的部分：

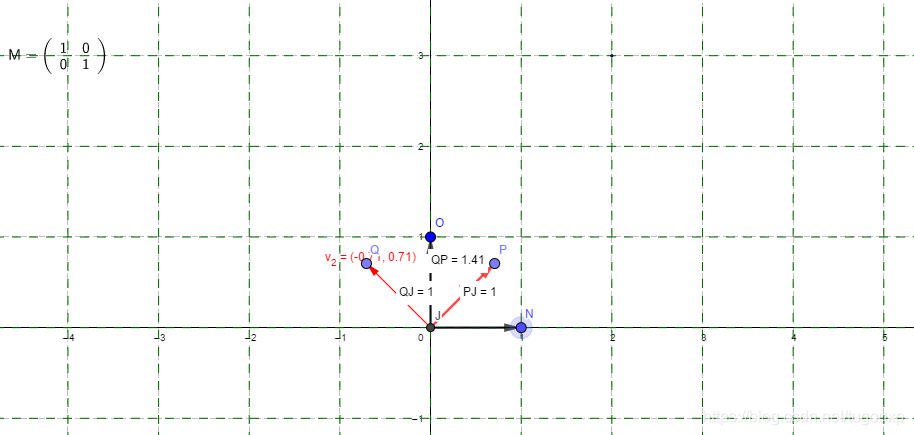
我们将线性变换施加于坐标轴单位向量，得到下图，如图，经过线性变换A， 特征向量长度变为原来的3倍和5倍，方向不变。

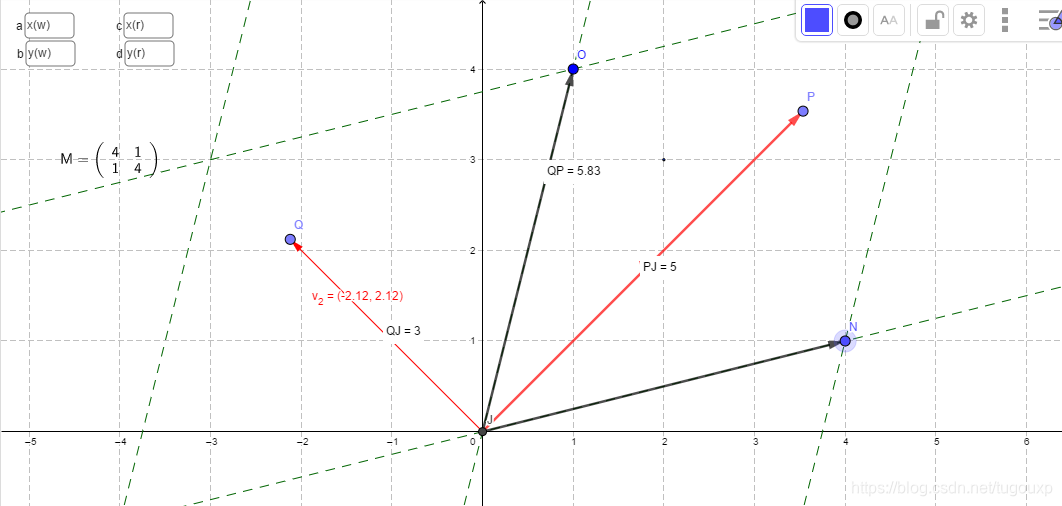
经过两次线性变换：

特征向量再次扩大特征值的倍数。

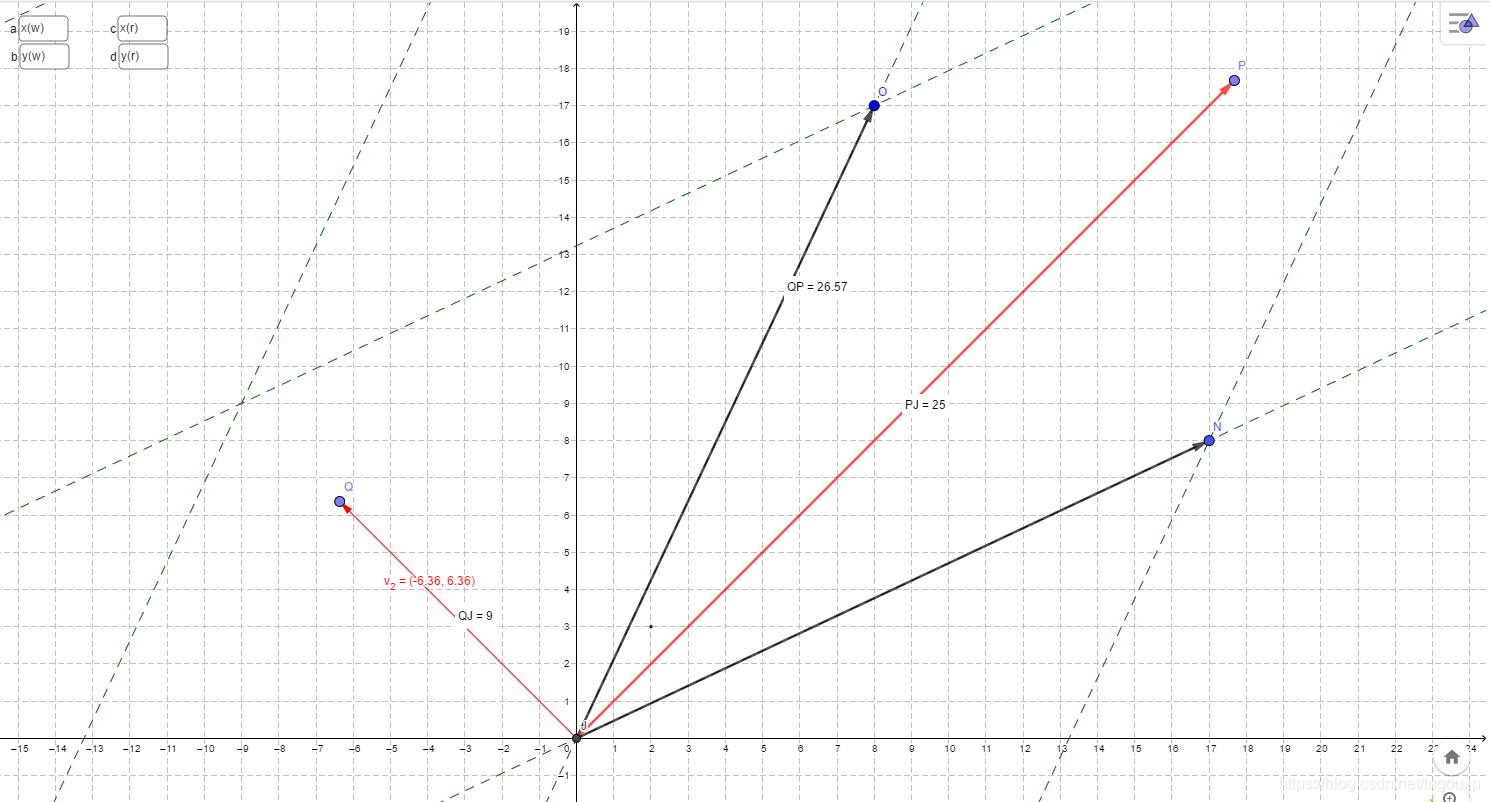
对于任意向量，设其v世界坐标为(2,3),

转换到标准坐标系为

 

 

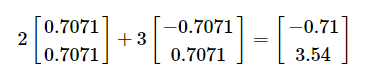
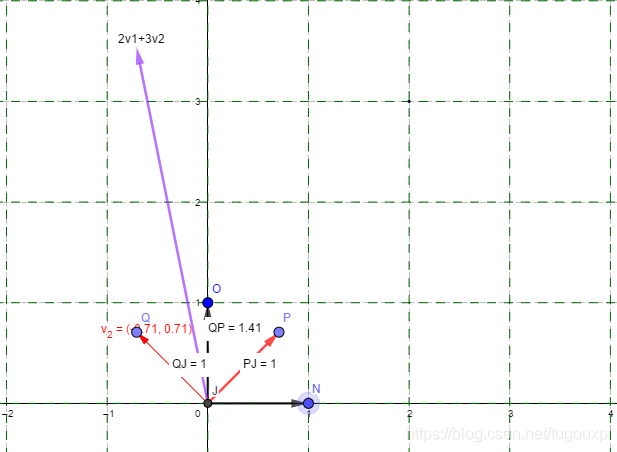
变换后呢

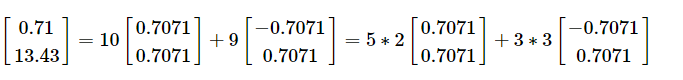
横纵坐标轴分别变为原来的5倍和3倍，正好是特征值。

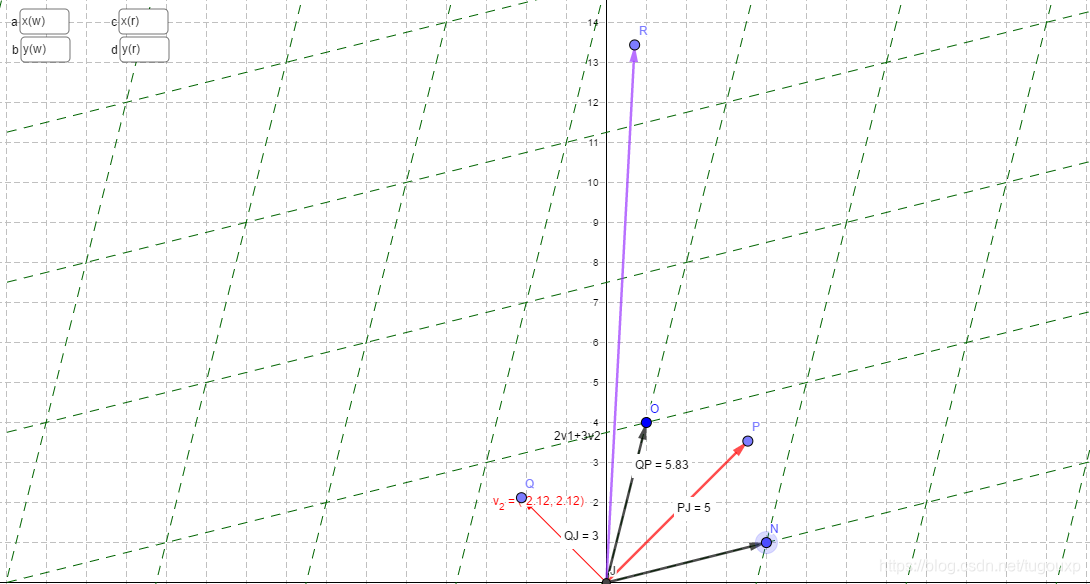
现在我们换一个坐标系，看一下同样的线性变换，新的坐标系中的变换矩阵是什么样子

设新坐标系:

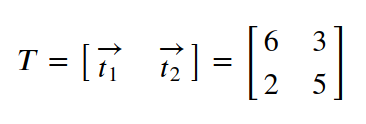
其中某点T在原坐标系的坐标为,(5.5,3.3)

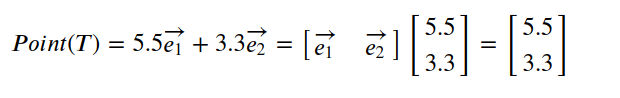
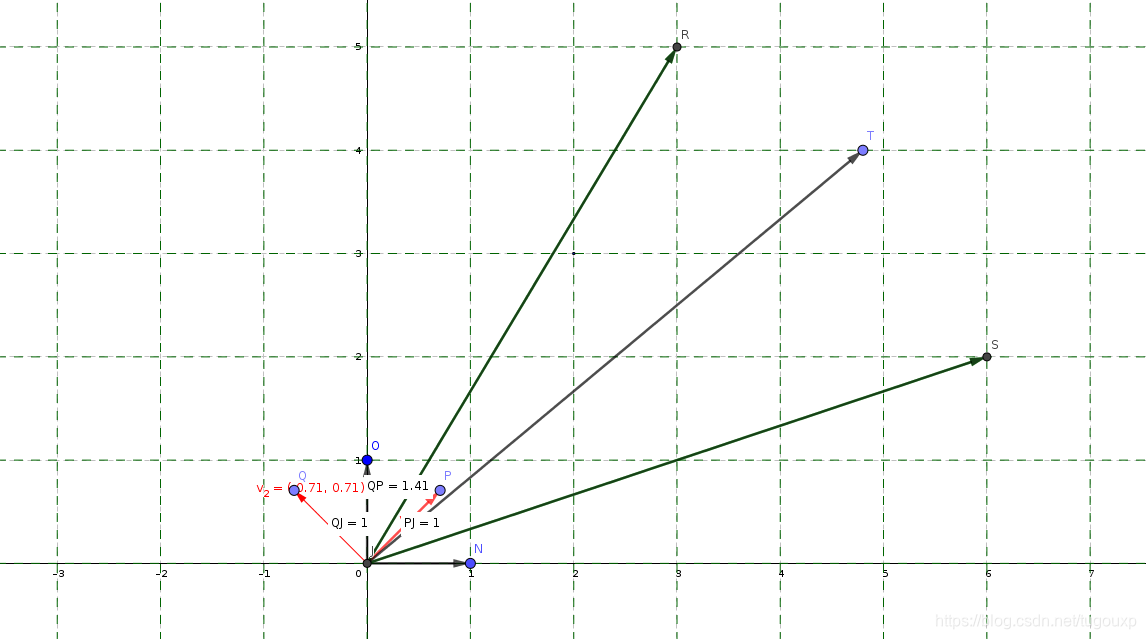
经过线性变换后:

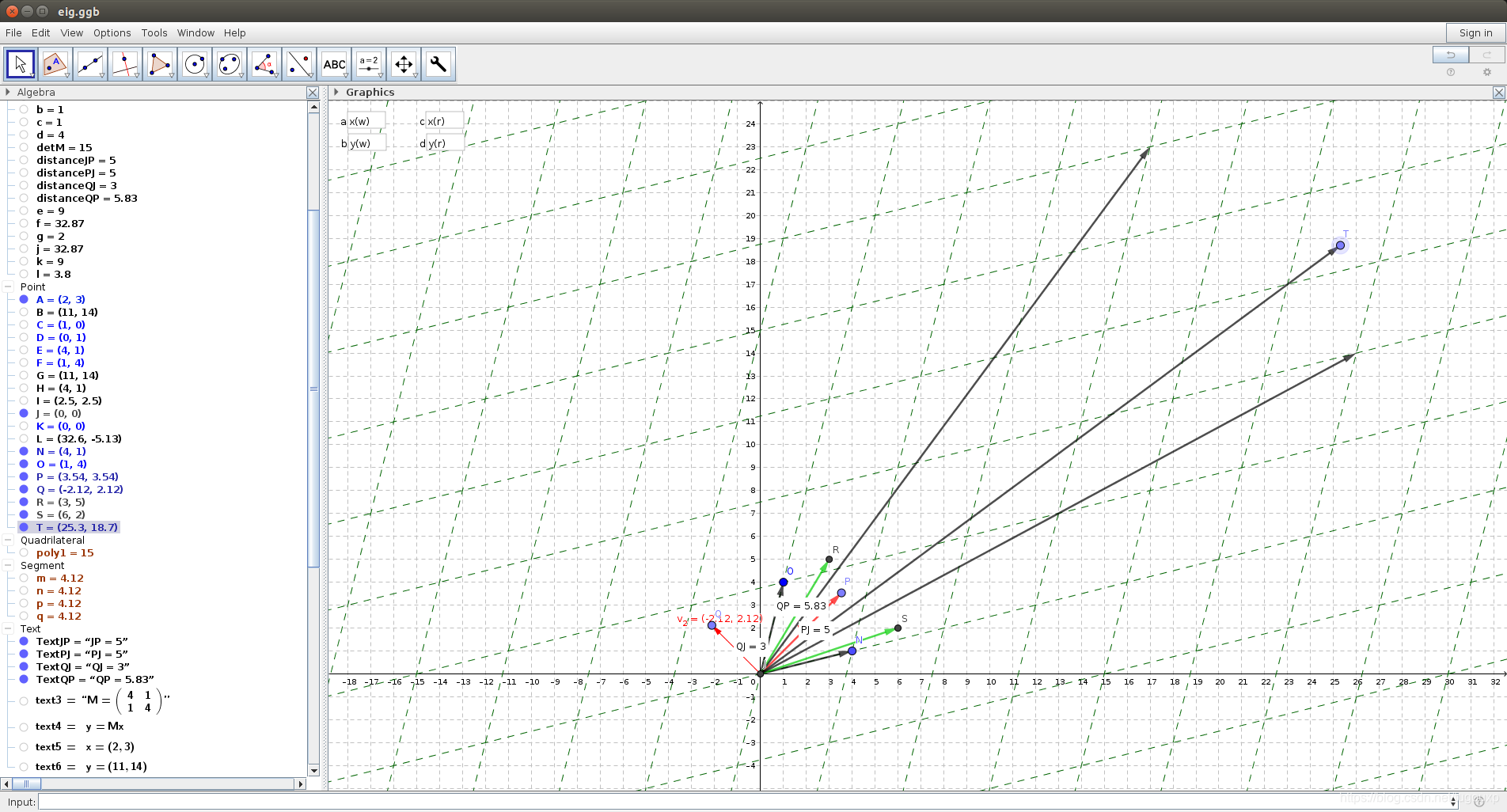
坐标变为

则新坐标轴下的线性变换可表示为：

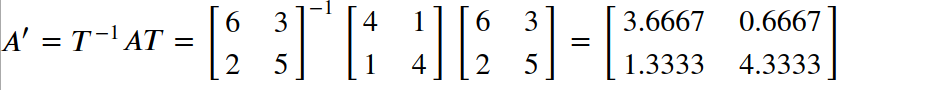
测试等式成立,A`确实是新坐标系下的对等变换：

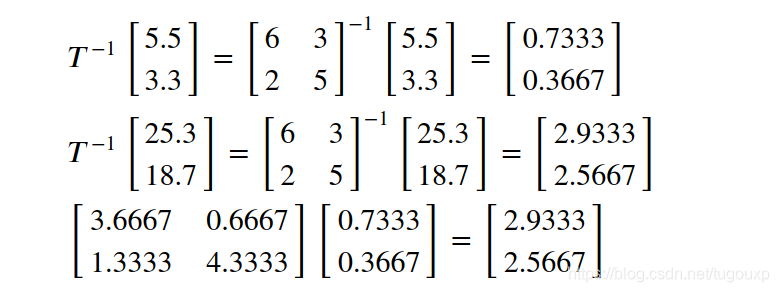
新的线性变换对应的特征向量和特征值为：

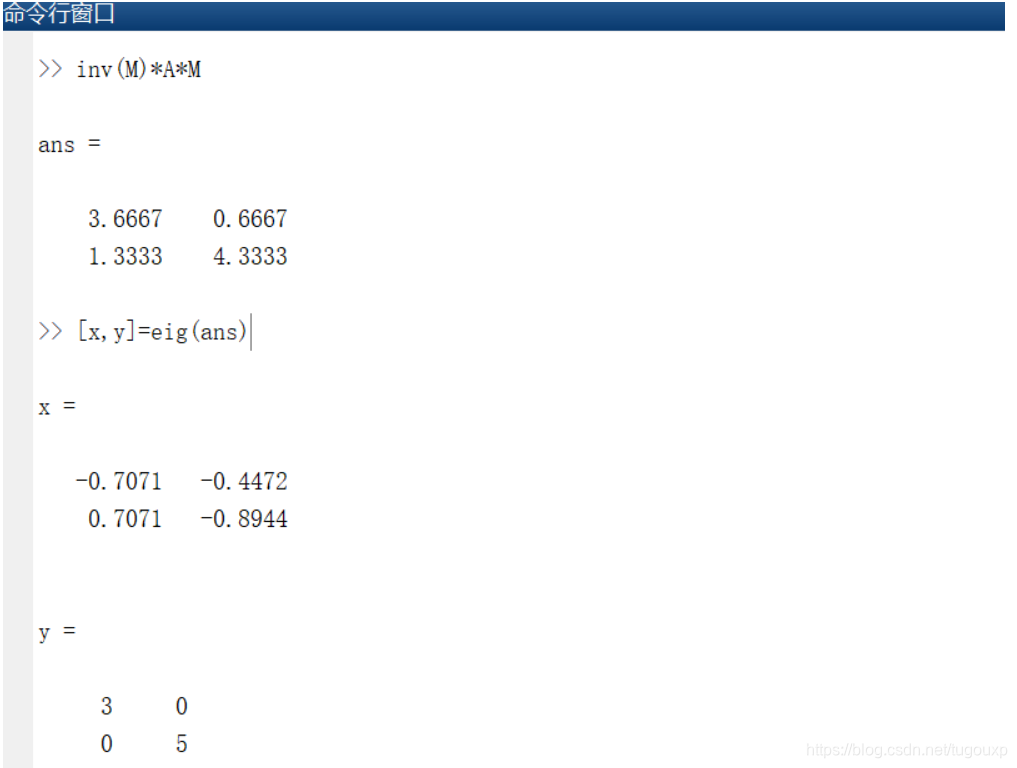
可见相似矩阵的特征值是相同的，但是特征向量明显不同，这是合理的，特征向量坐标依赖于基的选择，而且可以理论推导出，相似矩阵的特征向量之前满足简单的线性变换关系.

特征多项式相同，所以特征值一定相同：

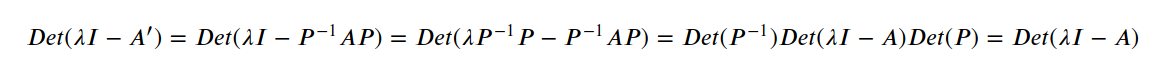特征向量不同，差着一个线性变换:

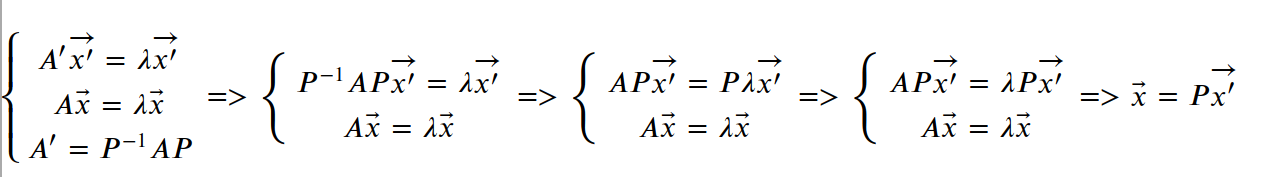
验证:　ans归一化后得到的特征向量和A矩阵是相同的，相似矩阵的特征向量的方向相同，特征值完全相同。

图形仿真的结果和理论推导完全吻合。

最后一个问题，上面已经得到结论，互为相似的矩阵表示的是同一个线性变换，只是在不同的坐标系下的观察角度不同，那么，如果已经知道两个矩阵是相似的(具有相同的特征值)，那么有没有办法得到两个矩阵的坐标系呢？

例如:

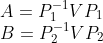
由于相似性是等价关系，A 和 B 都和V相似，那么A和B一定相似，A,B是相似矩阵，和 代表两个矩阵到V矩阵的相似变换，其本质是从线性变换V所在的基向线性变换A或B所在的基的过渡矩阵，初始基可以是任意的线性无关的基，不要求必须是单位正交基，对于任何初始机中的线性变换V，相似的形式都保持不变。

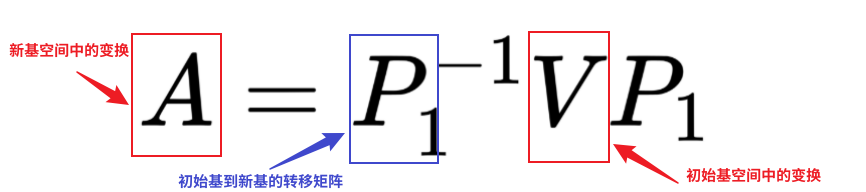
则存在Ｐ，使得:

P就应该是Ｂ变换对应的坐标系，应该是多少呢？由:

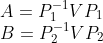
得到:

所以

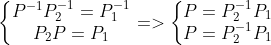
同理，从Ｂ的角度

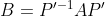
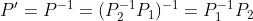
octave 举例如下：

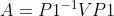
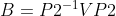
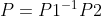
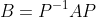
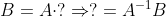
如同A和V以及B和V矩阵同转移矩阵P_1,P_2一样，A和B之间的相似变换对应的转移矩阵就是， 它描述了线性变换在两个不同基下的坐标转换关系。具体来说，假设矩阵 A 和 B 代表同一个线性变换 T，但分别基于不同的基：

• 设矩阵 A 是线性变换 T 在基 U 下的表示。

• 设矩阵 B 是线性变换 T 在基 W 下的表示。

• 矩阵V是线性变换T在参考基下的表示，如前所述，参考基可以是任意基，不需要正交。

P 是从基 W（即 B 所在的基）到基 U（即 A 所在的基）的坐标变换矩阵。也就是说，对于任意向量 x，如果它在基 W 下的坐标为 ​，那么在基 U 下的坐标为

.

反过来，从基 U 到基 W 的变换矩阵是，即:

所以，根据相似矩阵，也可以算得两个坐标系之间的转移矩阵．相似性的形式和初始参考基（对应同一个线性变换V所在的基）是否是正交基无关。比如，我们忘掉V矩阵，从B矩阵开始推演，我们已经知道了如下成立：

我们再给B定义一个相似矩阵C，满足：

可以看到，形式和上面完全相同，只是初始矩阵从V变成了B，而变换B所在的基我们知道是非正交的，但是整个推导过程并不依赖任何正交性，我们依然能够推导出：

所有的基都是等价的，不存在绝对优先的坐标系，从使用性上会存在更加方便的坐标系（标准正交坐标系，否则数学就不会教变换坐标系简化问题的方法了），但是不存在绝对的参考系。

基变换不会让你学过的那些描述线性变换“几何本质”的公式发生任何改变。比如行列式，秩等，但是，那些依赖于坐标系的具体“计算公式”（尤其是涉及内积和长度的），其形式必须根据新的基进行调整（引入度量张量），尽管它们所描述的几何关系本身是永恒的。这正体现了线性代数的美妙之处：它严格区分了客观的、不变的几何本质，和主观的、可变的坐标表示。

不得不说，简单的逻辑蕴含着深刻的对称性原理，数学就是抓住本质的工具,　线性代数是非常有用的一门学科，即便对于非理工科的同学，里面的线性变换，矩阵，特征根，特征向量的概念对于塑造我们的世界观也有很大作用，可是呢，我们的线代教育上来就先介绍行列式，然后就是灌输一些毫无道理的规则，这对于喜欢对问题追根究底的同学是种折磨。

人类是什么时候开始意识到坐标系可以不用垂直正交的呢？

验证：

验证思路如下字符图所示：

+-----------------------------------------------------+
|                     初始基 E                         |
+-----------------------------------------------------+
|                     线性变换 T                       |
+-----------------------------------------------------+
          ^                            ^
          |                            | 
+-------------------+          +-------------------+
|                   |          |                   |
|  矩阵表示: V       |<-------->|   矩阵表示: V       |
|                   |          |                   |
+-------------------+          +-------------------+
          ^                            ^
          |                            |
          | P1                         | P2
          | (从基U到E的过渡矩阵)          | (从基W到E的过渡矩阵)
          |                            |
+-------------------+          +-------------------+
|                   |          |                   |
|   新基 U           |          |   新基 W          |
|                   |          |                   |
|  矩阵表示: A       |          |  矩阵表示: B        |
|  A = P₁⁻¹ V P₁    |          |  B = P₂⁻¹ V P₂    |
|                   |          |                   |
+-------------------+          +-------------------+
          ^                            ^
          |                            |
          | P⁻¹ = P₁⁻¹ P₂              | P = P₂⁻¹ P₁
          | (从基W到基U的过渡矩阵)        | (从基U到基W的过渡矩阵)
          |                            |
          +----------------------------+
                       |
                       v
                   A = P⁻¹ B P

设线性变换V为相对于标准正交基将坐标平面逆时针旋转90度

应用变换示意图：

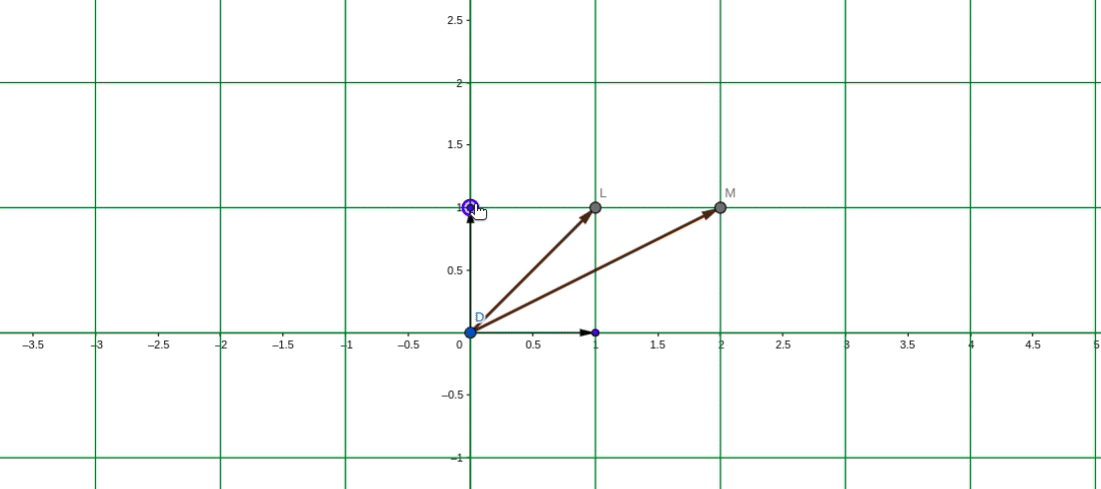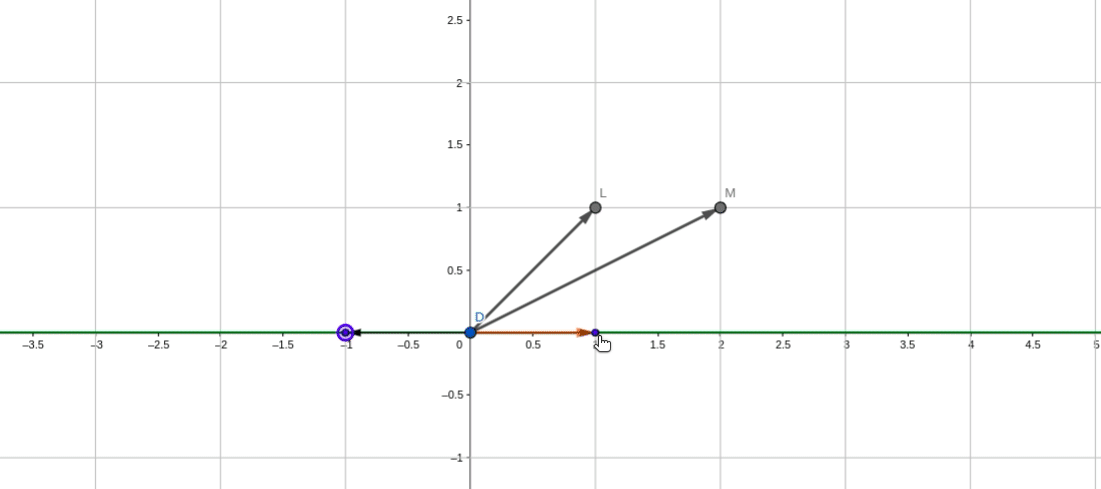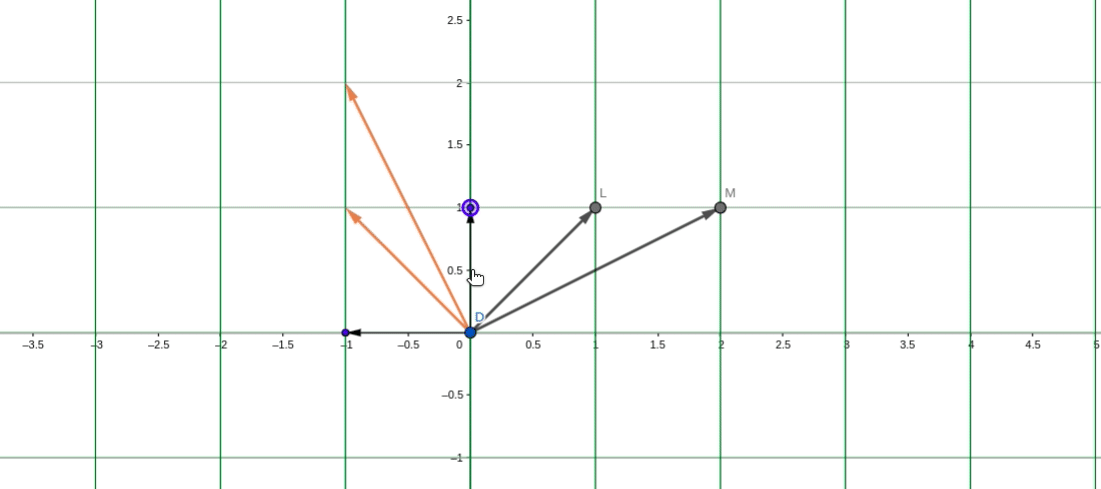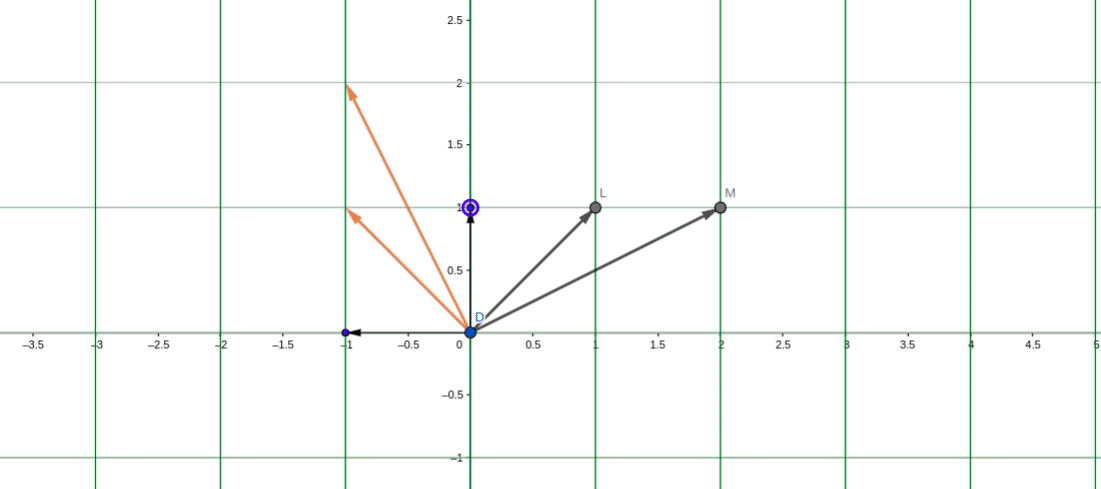
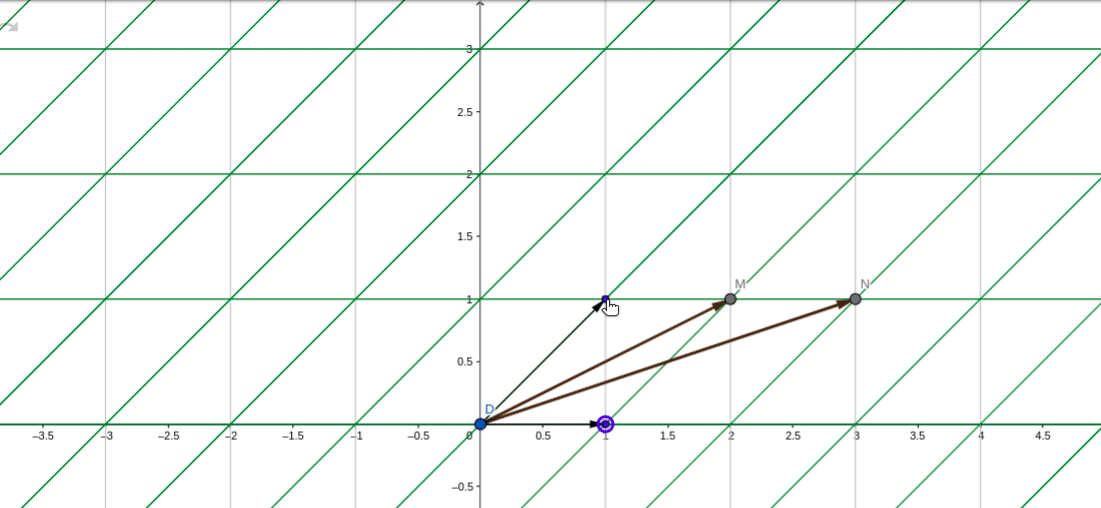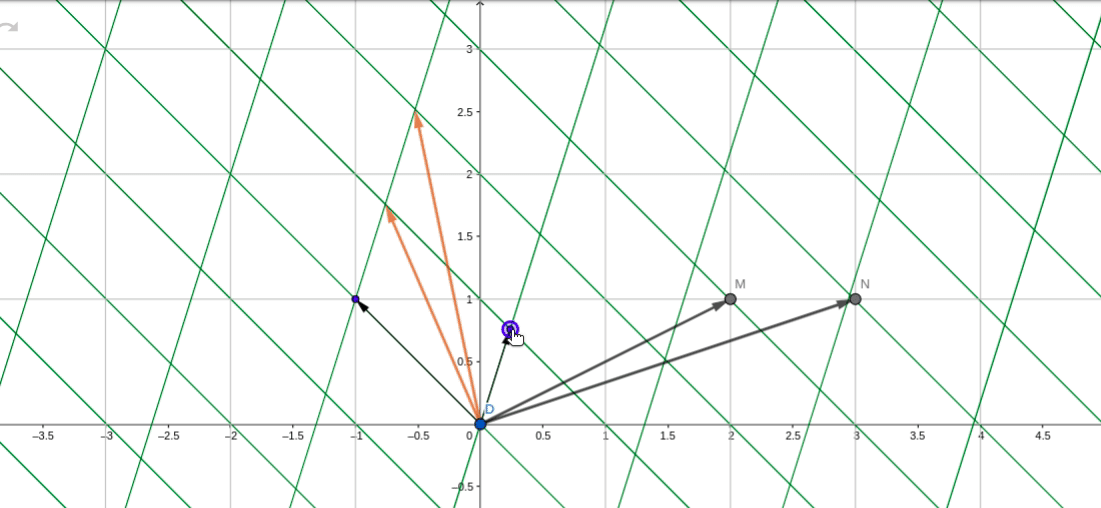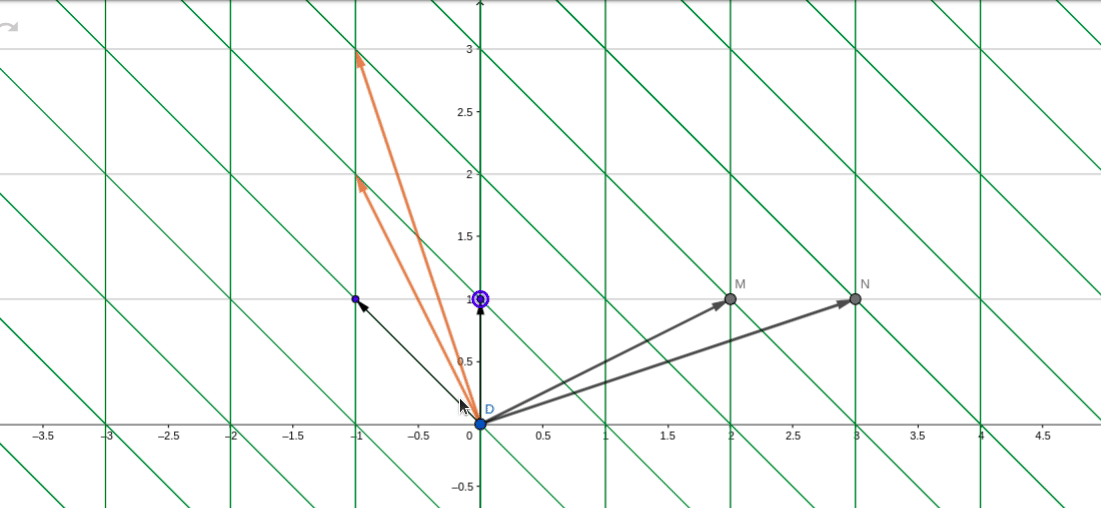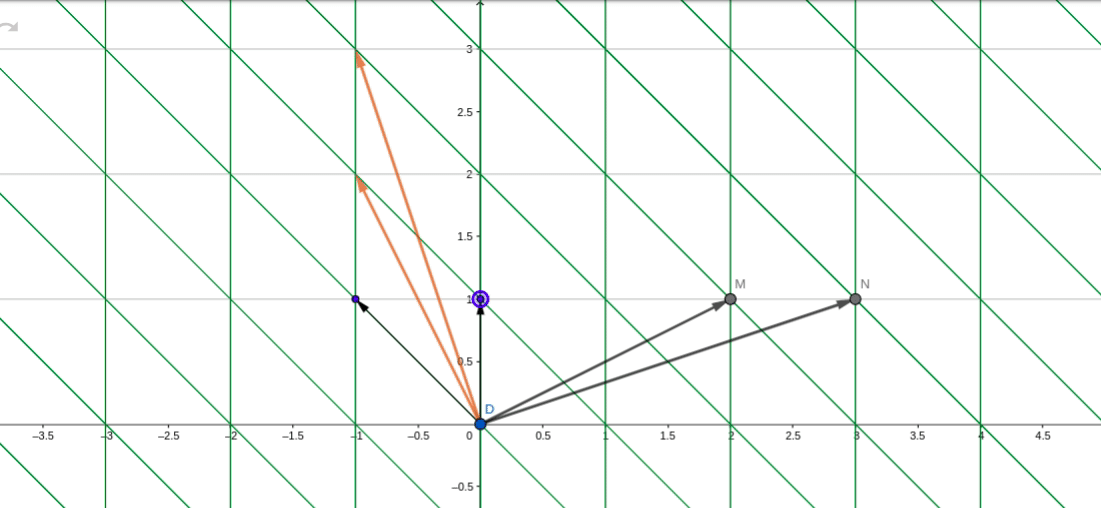
在转移矩阵P_1下，P_1为剪切矩阵：

在剪切矩阵为基的平面下，对应的逆时针旋转90度的线性变换变为：

其中分别表示在剪切基下的变换坐标，所以，在基下，A变换后的坐标位置分别为：

最终还是以初始基坐标为锚点,坐标轴也同样顺时针旋转了90度。

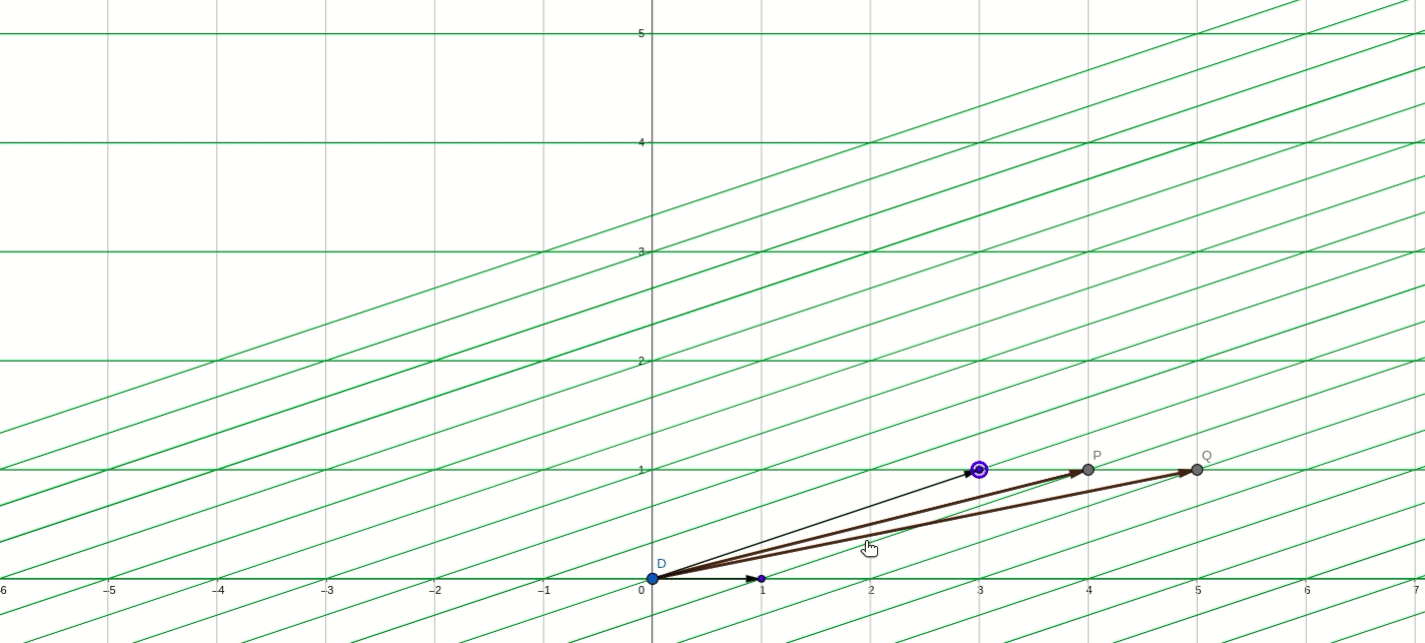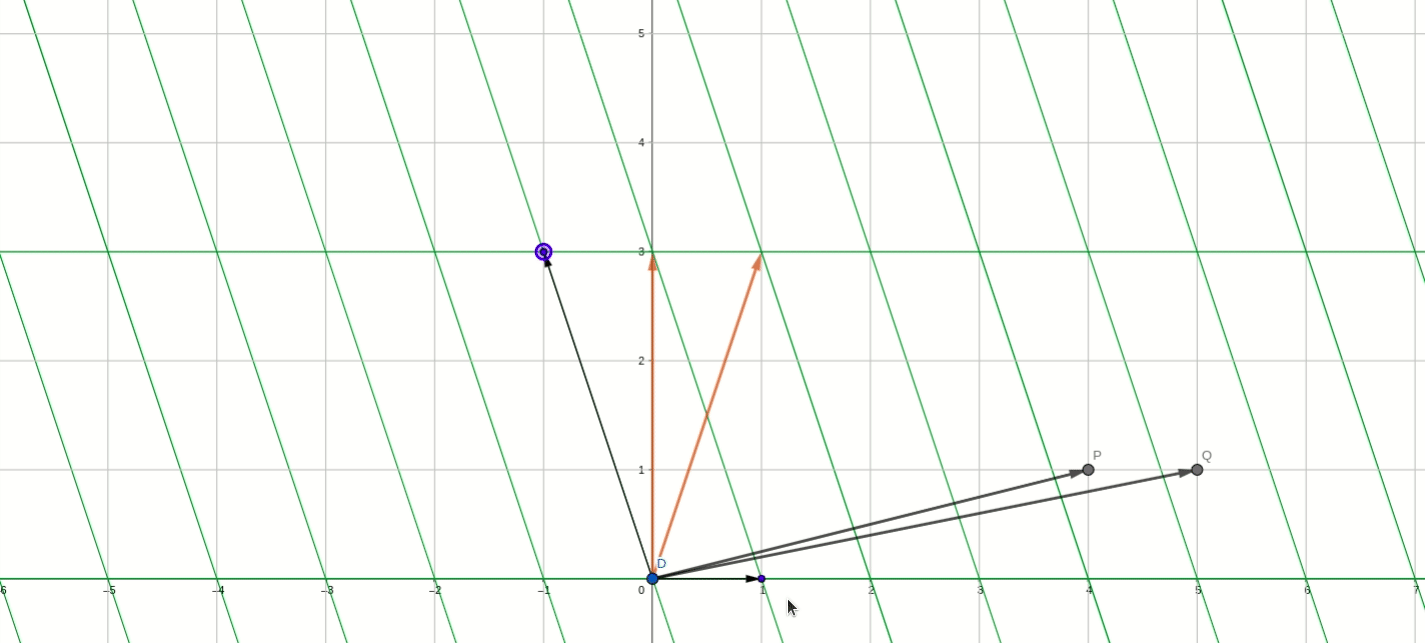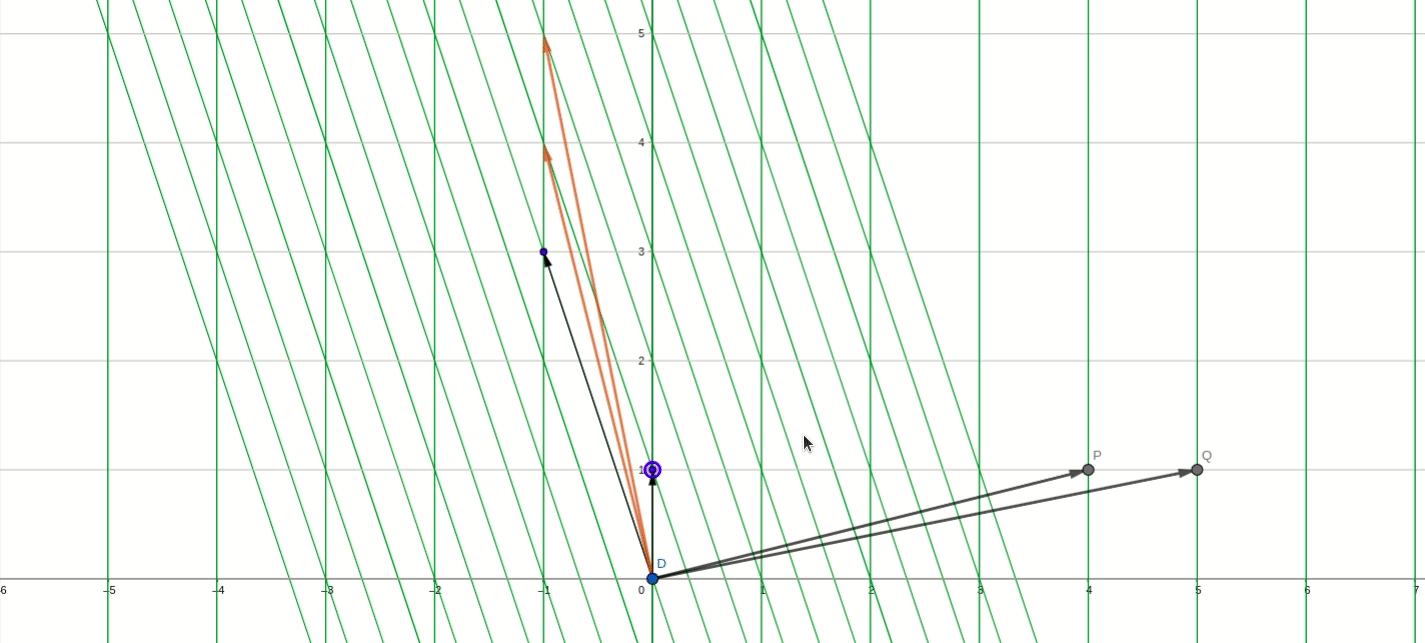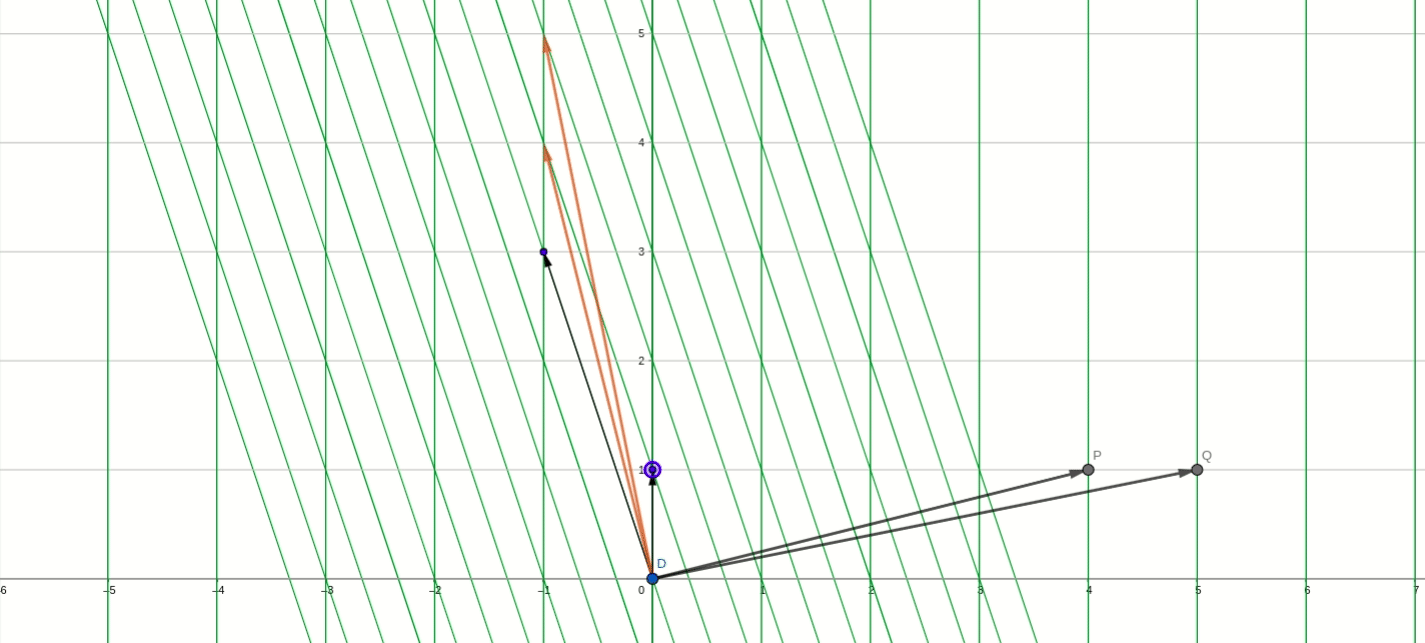
在转移矩阵P_2下，P_2矩阵：

其中分别表示在基下的变换坐标，所以，在基下，经过B变换后的坐标位置分别为：

最终还是以初始基坐标为锚点,坐标轴也同样顺时针旋转了90度。

由前面推导可知

计算得到：

那么P到底有什么几何含义呢？

假设A变换所在坐标系下的一个坐标向量为

因为A的基（相对于标准正交坐标系）为：

所以，从标准正交基的视角来看，其坐标为

因为：

因为B的基为：

所以看出来了吗，线性变换A所在的坐标系下的向量对应的在标准正交基下的同一个向量的坐标是，这个和线性变换B下的坐标竟然是同一个位置，而是怎么来的呢？它是A变换所在坐标系下的坐标做乘P矩阵得到的，所以，P矩阵的意义就非常清除了，P举着实际上是A变换所在坐标系和变换所在坐标系的转移矩阵。

实际上，以上推导完全不依赖V所在的初始坐标系是正交系，任何合法初始坐标系都可以，关键在最后一步：

这里用正交坐标系作为V所在的初始坐标系目的是为了方便绘制动画。为了证明这一点，我们从非标准正交基开始从新做这个数学实验：

设初始基向量分别为：

新基是剪切矩阵的两个列向量，线性变换仍然是逆时针旋转90度，在新基下的表示为：

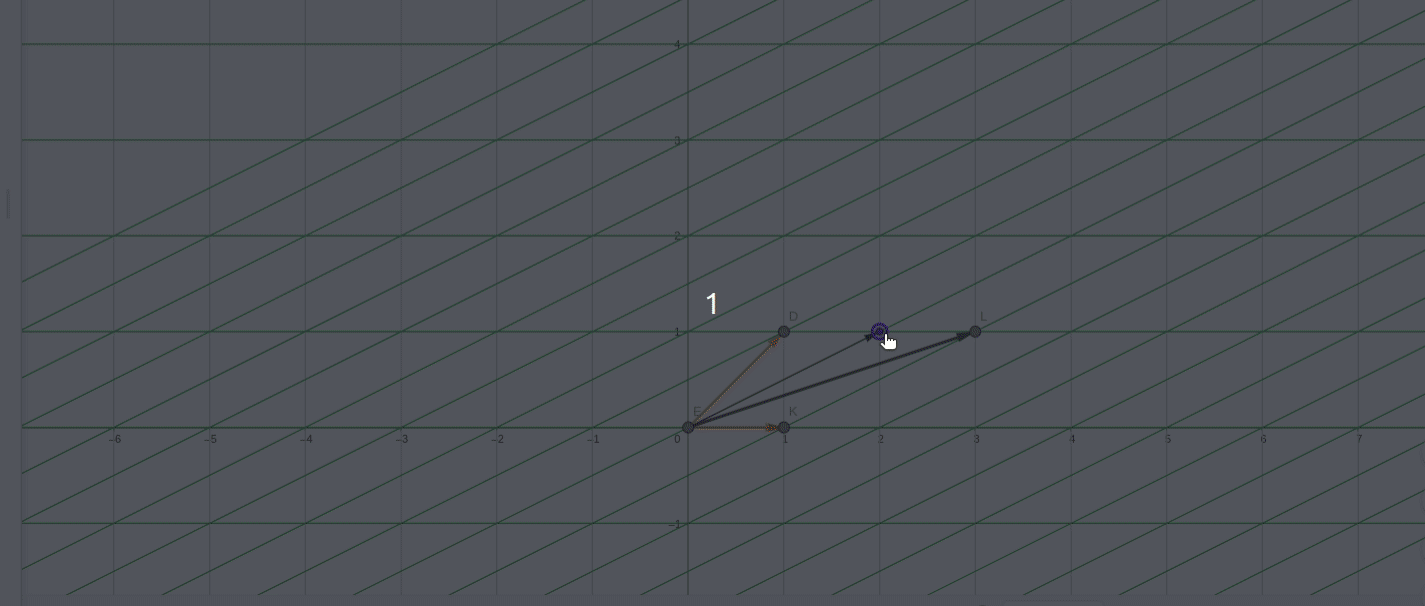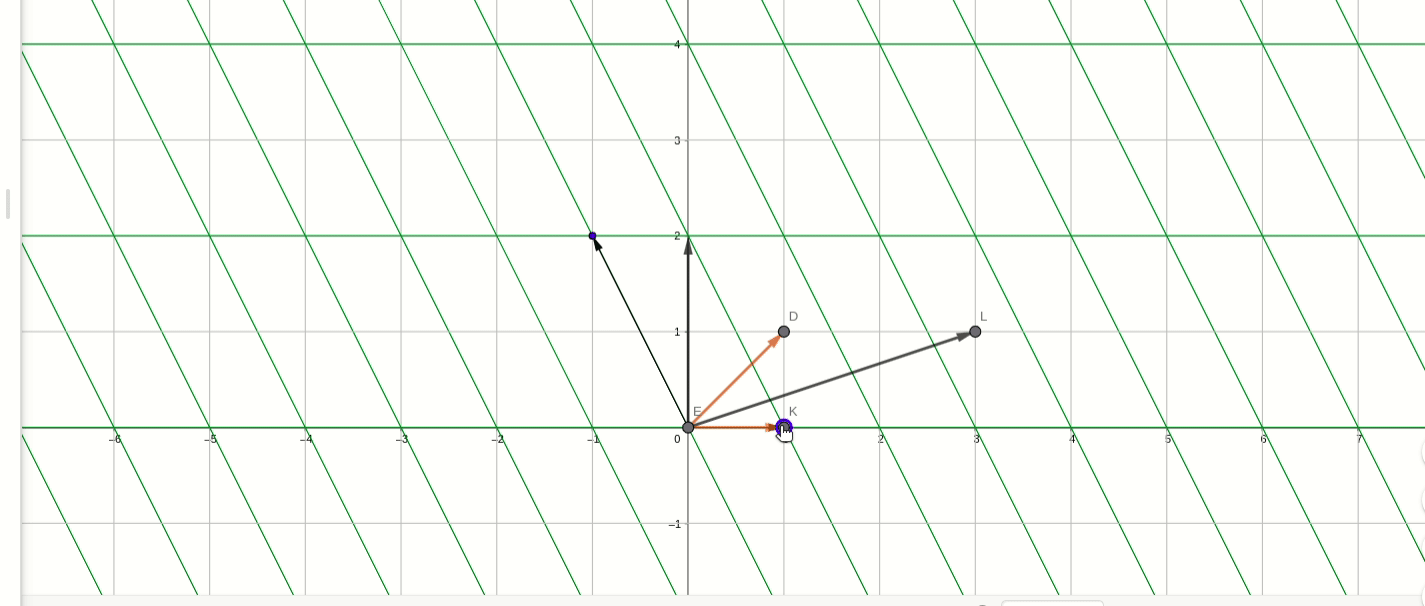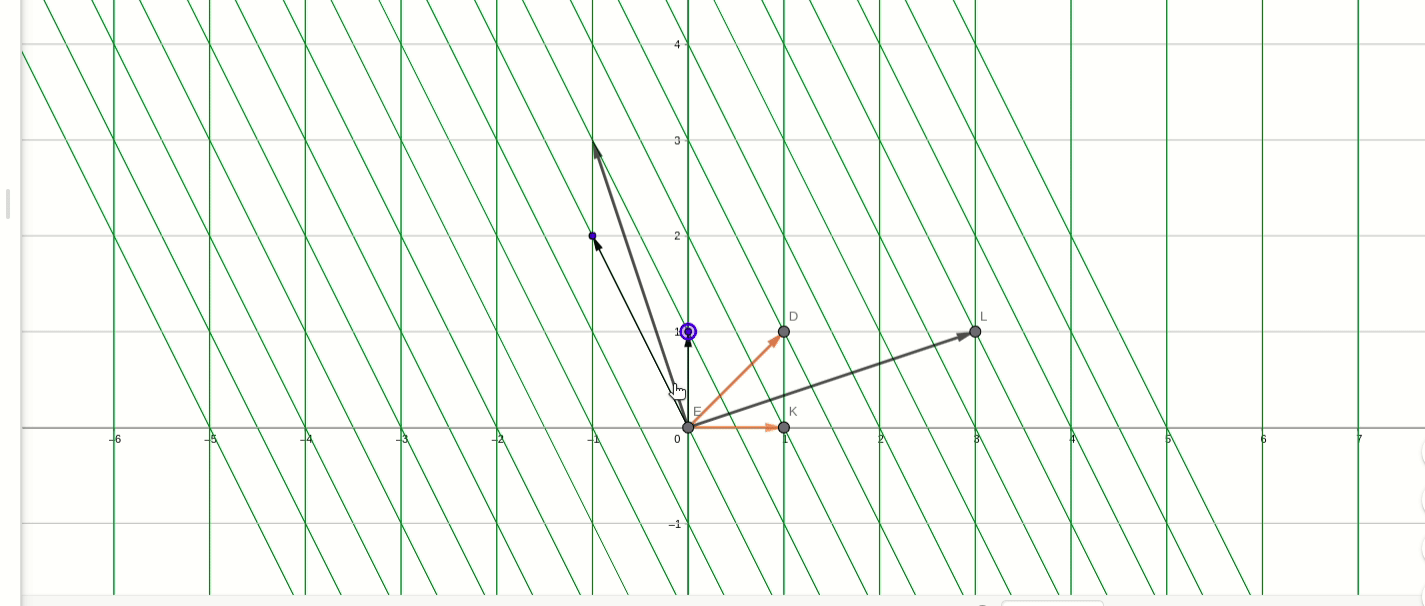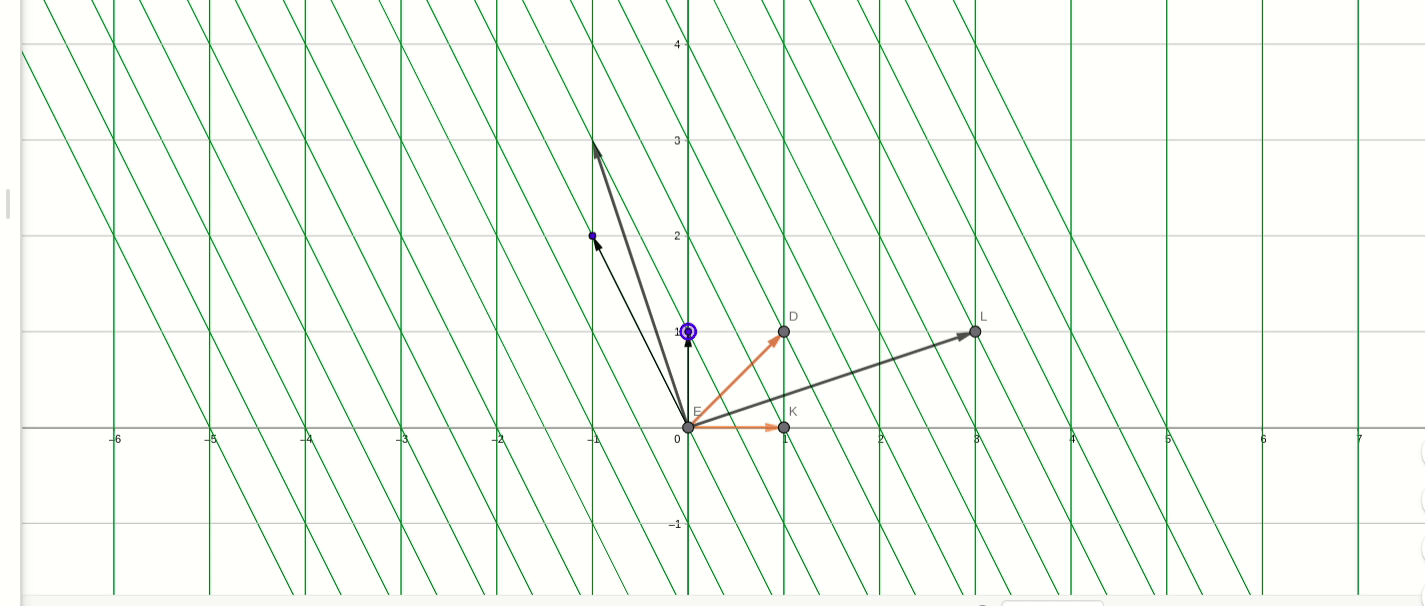
同样， 设第一个基变换矩阵为P_1,相对于初始基下的表示为：

红色的初始基，移动的是新基，新基在初始基下的坐标是P_1的列向量，可以看到，新基在经过A变换的效果就是进行逆时针90度旋转。

在转移矩阵P_2下，P_2矩阵：

红色的初始基，移动的是新基，新基在初始基下的坐标是P_2的列向量，可以看到，新基在经过B变换的效果就是进行逆时针90度旋转。

由前面推导可知:

计算得到：

下面看一下，在初始坐标系为非正交情况下，P矩阵的几何含义。假设A变换所在坐标系下的一个坐标向量为：

因为A的基（相对于初始剪切矩阵坐标系）为：

所以，从初始剪切矩阵坐标系来看，其坐标为

因为：

因为B的基相对于初始剪切矩阵坐标系）为：

所以可以看到，初始基向量的改变不影响计算结果，我们在考虑线性变换的时候，可以不用过问初始基向量是多少，线性变换的复合方法和基向量是什么无关。

如下图所示，基P下的坐标(x,y)是相对于初始基的不动点，也就是说：

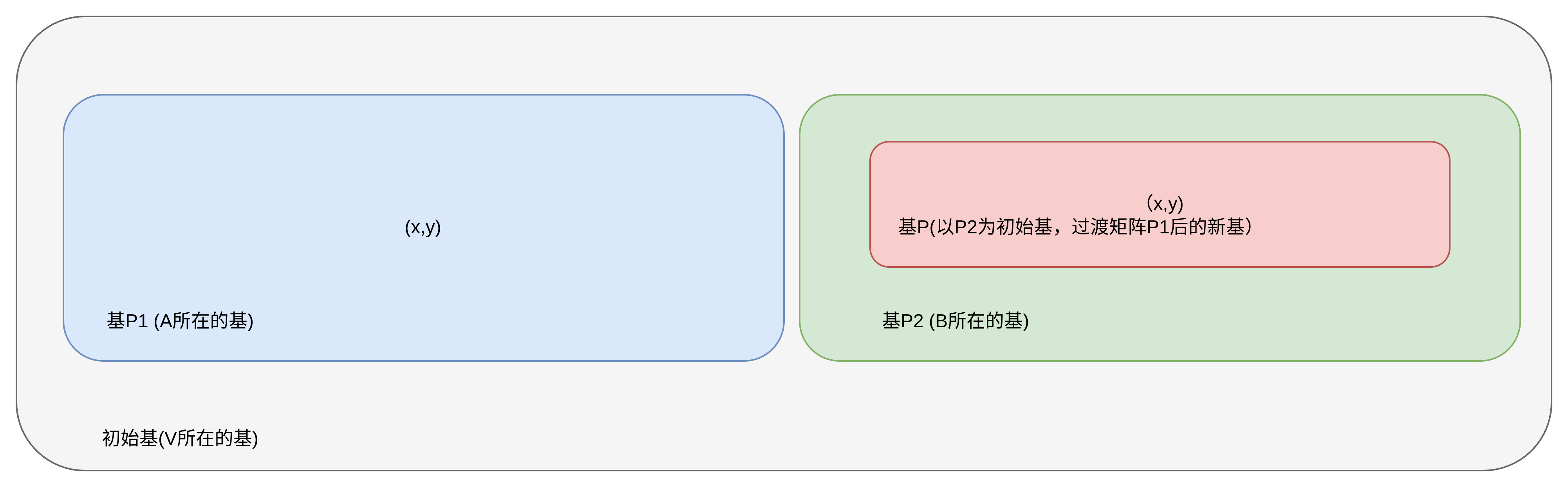
初始基可以是非正交基，不要求是标准正交基，抽象角度，对于坐标(x,y)，满足如下金字塔坐标系的基变换公式，其中下一级的基变换矩阵是相对于上一级的坐标系而言的：

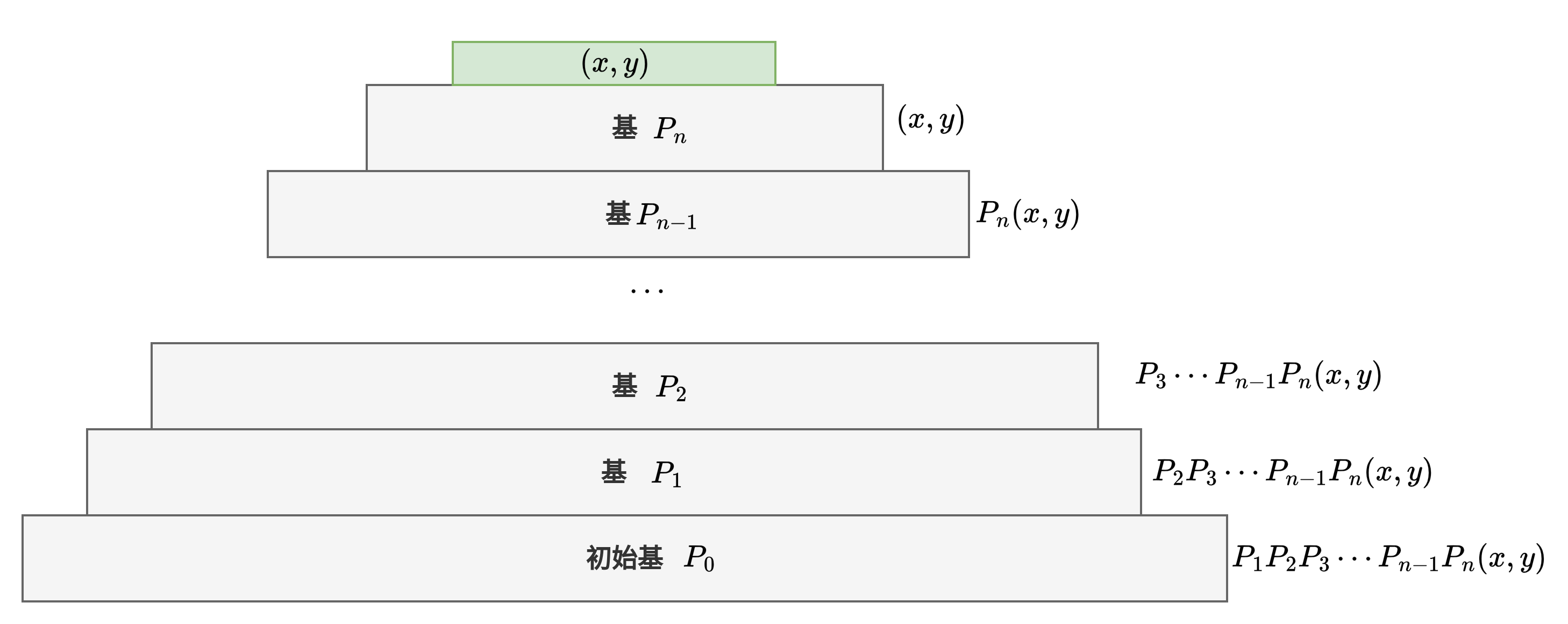
更一般的结论是，如果存在一个从标准正交基开始的基链，其中初始基变换的转移矩阵为 P0​，后续每个新基都是通过对上一个基应用线性变换矩阵得到的，转移矩阵依次为 P1,P2,…,Pn。矩阵 Pi​ 表示从第 i 个基到第 i−1个基的过渡矩阵，也就是说，如果有一个向量在第i个基下的坐标为,那么它在第i-1个基下的坐标为：

现在，在第 n 个基下有一个坐标点(x_n,y_n),要找到改点在初始正交坐标系下的坐标，通过基变脸链条，坐标点从第n个基变换到初始正交基的坐标计算方法为：

乘积得到一个新的列向量，即点在初始基下的坐标，这个公式表示过渡矩阵的连续应用相当于将坐标从高级基转换回初始基，其中每一步的转移矩阵P_i都是可逆的。

总结：

1.特征值是反映变化速度的量，反映了在多个变化因素里，谁占主导地位，谁决定了变化的速度
2.特征向量是反映稳定性的量，决定了变化的宿命,即决定了它最终向谁收敛。

结束！