【数据结构与算法】第四章：高级排序

于 2021-09-15 07:25:17 发布
阅读量228 收藏
点赞数
分类专栏： 数据结构与算法 文章标签： 算法 数据结构 java
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/tu_wer/article/details/120300640
版权

基础排序：冒泡排序、选择排序、插入排序，在最坏情况下的时间复杂度都是O(N^2)，平方阶，随着输入规模的增大，时间成本将急剧上升，所以这些基本排序方法不能处理更大规模的问题

4.1、希尔排序

希尔排序是插入排序的一种，又称“缩小增量排序”，是插入排序算法的一种更高效的改进版本

案例：

  • 需求 ： 排序前：{9,1,2,5,7,4,8,6,3,5} 排序后：{1,2,3,4,5,5,6,7,8,9}

  • 排序原理

    1. 选定一个增长量h，按照增长量h作为数据分组的依据，对数据进行分组

    2. 对分好组的每一组数据完成插入排序

    3. 减小增长量，最小减为1，重复第二步操作

  • 增长量h规则
// 确定增长量h的最大值
int h = 1
while(h < 数组长度/2){
	h = 2h + 1；
}


// 增长量h的减小规则
h = h/2

关于 2h+1 和 h/2：

在堆中(完全二叉树)，结点 h 的两个子结点为 2h 和 2h+1，父结点为 h/2

  • API设计

  • 代码实现
import java.util.Arrays;

/**
 * @author 土味儿
 * Date 2021/10/5
 * @version 1.0
 * 希尔排序
 * 插入排序的优化版
 */
public class Shell {
    /**
     * 比较次数
     */
    private static int g_num = 0;
    /**
     * 交换次数
     */
    private static int e_num = 0;

    /**
     * 排序
     *
     * @param a
     */
    public static void sort(Comparable[] a) {
        // 【1】根据数组长度，确定增长量h的初始值
        int h = 1;
        while (h < a.length / 2) {
            h = 2 * h + 1;
        }

        // 【2】希尔排序
        while (h > 0) {
            // 【2.1】找到待插入元素
            for (int i = h; i < a.length; i++) {
                // 【2.2】把待插入元素放入有序数组中
                for (int j = i; j - h >= 0; j -= h) {
                    // 待插入元素是a[j]；比较a[j]、a[j-h]
                    if (greater(a[j - h], a[j])) {
                        // 前面大于后面，交换
                        exch(a, j - h, j);
                    } else {
                        // 前面不大于后面，退出内循环
                        break;
                    }
                }
            }

            // 【2.3】减小增长量h的值，继续下次操作
            h = h / 2;
        }
    }

    /**
     * 判断元素v是否大于w
     *
     * @param v
     * @param w
     * @return
     */
    private static boolean greater(Comparable v, Comparable w) {
        g_num++;
        return v.compareTo(w) > 0;
    }

    /**
     * 交换数组c中位置i和j处的元素
     *
     * @param c
     * @param i
     * @param j
     */
    private static void exch(Comparable[] c, int i, int j) {
        if (c[i] != c[j]) {
            e_num++;
            Comparable temp = c[i];
            c[i] = c[j];
            c[j] = temp;
        }
    }

    public static void main(String[] args) {
        Integer[] c = {9, 1, 2, 5, 7, 4, 8, 6, 3, 5};
        System.out.println("排序前：" + Arrays.toString(c));
        sort(c);
        System.out.println("排序后：" + Arrays.toString(c));

        System.out.println("比较次数：" + g_num);
        System.out.println("交换次数：" + e_num);
    }
}

排序前：[9, 1, 2, 5, 7, 4, 8, 6, 3, 5]
排序后：[1, 2, 3, 4, 5, 5, 6, 7, 8, 9]
比较次数：33
交换次数：17

  • 时间复杂度分析

    在希尔排序中，增长量h并没有固定的规则，在这里就不做分析了。
    可以使用 事后分析法 对希尔排序和插入排序做性能比较。

  • 性能测试

    从100000到1的逆向数据，可以根据这个批量数据完成测试。

    测试的思想：记录排序前后的时间差

public class SortTest {
    /**
     * 比较插入排序和希尔排序
     */
    @Test
    public void testInsertionAndShell() {
        Integer[] c = getArray(10_0000);
        long start = System.currentTimeMillis();
        //InsertionSort.sort(c);//用时：17683
        ShellSort.sort(c);//用时：27
        long end = System.currentTimeMillis();
        System.out.println("用时：" + (end - start));
    }

    /**
     * 得到待排序数组
     * 最坏情况（倒序，从大到小）
     *
     * @param n
     * @return
     */
    private Integer[] getArray(int n) {
        Integer[] c = new Integer[n];
        for (int i = 0; i < n; i++) {
            c[i] = n - i;
        }
        return c;
    }
}

插入排序用时：17683
希尔排序用时：27

通过测试发现，在处理大批量数据时，希尔排序的性能明显高于插入排序

4.2、归并排序

1）递归

  • 定义： 定义方法时，在方法内部调用方法本身，称之为递归
public void show(){
    System.out.println("aaaa");
    show();
}
  • 作用
    它通常把一个大型复杂的问题，层层转换为一个与原问题相似的，规模较小的问题来求解。递归策略只需要少量的程序，就可以描述出解题过程所需要的多次重复计算，大大地减少了程序的代码量
  • 注意事项
    在递归中，不能无限制的调用自己，必须要有边界条件，能够让递归结束，因为每一次递归调用都会在栈内存开辟新的空间，重新执行方法，如果递归的层级太深，很容易造成 栈内存溢出

2）归并排序

归并排序是建立在归并操作上的一种有效的排序算法，该算法是采用 分治法 的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并

案例：

  • 需求: 排序前：{8,4,5,7,1,3,6,2} 排序后：{1,2,3,4,5,6,7,8}

  • 排序原理

    1. 尽可能的把一组数据拆分成两个元素相等的子组， 并对每一个子组继续拆分，直到拆分后的每个子组的元素个数是1为止

    2. 将相邻的两个子组进行合并成一个有序的大组

    3. 不断的重复步骤2，直到最终只有一个组为止

  • API设计

  • 归并原理

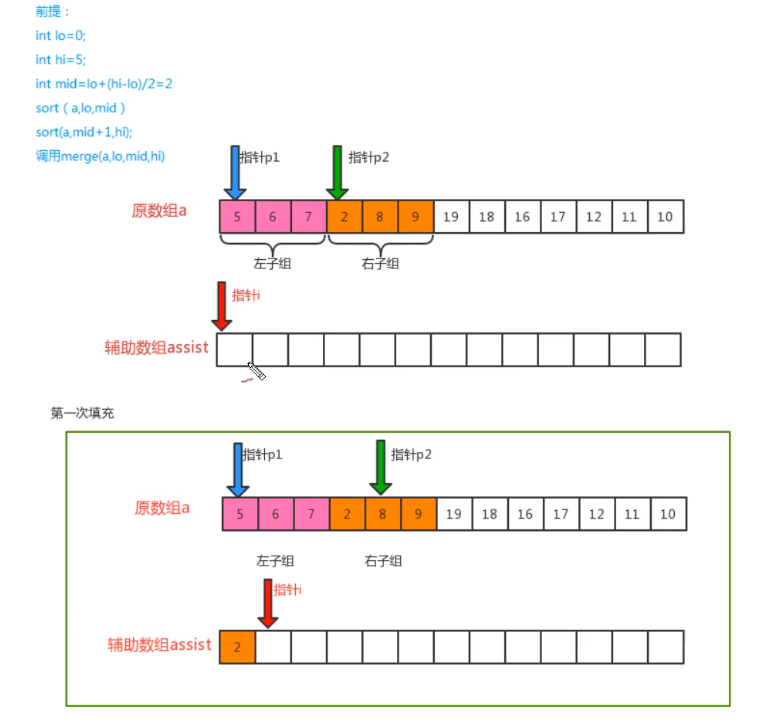
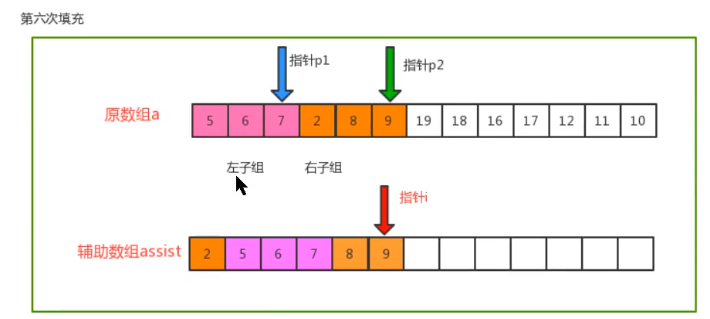
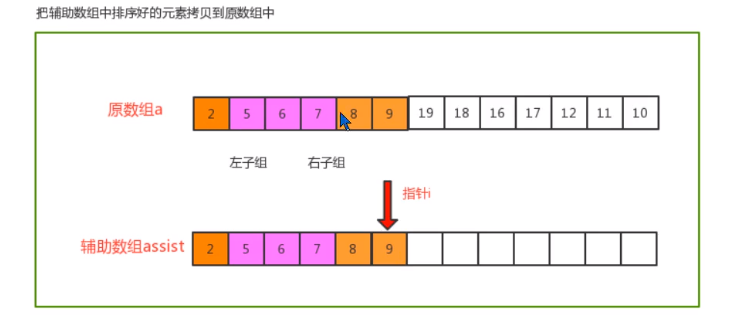
  • 代码实现
import java.util.Arrays;

/**
 * @author 土味儿
 * Date 2021/10/5
 * @version 1.0
 * 归并排序
 * 分而治之；递归
 */
public class Merge {
    /**
     * 辅助数组
     */
    private static Comparable[] assist;

    /**
     * 对数组c排序
     *
     * @param c
     */
    public static void sort(Comparable[] c) {
        // 【1】初始化辅助数组
        assist = new Comparable[c.length];

        // 【2】定义i,j；分别表示数组的边界索引
        int i = 0;
        int j = c.length - 1;

        // 【3】调用重载方法排序
        sort(c, i, j);
    }

    /**
     * 对数组c中位置i到j的元素排序
     * 递归；分而治之
     *
     * @param c
     * @param i
     * @param j
     */
    private static void sort(Comparable[] c, int i, int j) {
        // 【1】参数有效性检查
        if (j <= i) {
            // j<=i非常重要：是退出递归的必要条件；说明已经不能再分组了
            return;
        }

        // 【2】分组；找中间索引值m
        int m = i + (j - i) / 2;

        // 【3】递归排序
        sort(c, i, m);
        sort(c, m + 1, j);

        // 【4】合并
        merge(c, i, m, j);
    }

    /**
     * 数组c中，从 i 到 m 为一组，从 m+1 到 j 为一组，合并
     * 按顺序放入辅助数组中，再用辅助数组替换原数组对应位置
     *
     * @param c
     * @param i
     * @param m
     * @param j
     */
    private static void merge(Comparable[] c, int i, int m, int j) {
        // 【1】定义三个指针：辅助数组p0，左子数组p1，右子数组p2
        int p0 = i;
        int p1 = i;
        int p2 = m + 1;

        // 【2】遍历：移动p1、p2，比较索引位置的值，找出较小的值，放入辅助数组中
        while (p1 <= m && p2 <= j) {
            if (less(c[p1], c[p2])) {
                // p1小于p2，把p1的值存入辅助数组中，移动p0、p1
                assist[p0++] = c[p1++];
            } else {
                // p1不小于p2（大于或等于），把p2的值存入辅助数组中，移动p0、p2
                assist[p0++] = c[p2++];
            }
        }

        // 【3】遍历：如果p1没有走完，移动p1，顺序放入辅助数组中
        while (p1 <= m) {
            assist[p0++] = c[p1++];
        }

        // 【4】遍历：如果p2没有走完，移动p2，顺序放入辅助数组中
        while (p2 <= j) {
            assist[p0++] = c[p2++];
        }

        // 【5】用辅助数组替换原数组中相应位置的元素
        for (int p = i; p <= j; p++) {
            c[p] = assist[p];
        }
    }

    /**
     * 判断元素v是否小于w
     *
     * @param v
     * @param w
     * @return
     */
    private static boolean less(Comparable v, Comparable w) {
        return v.compareTo(w) < 0;
    }

    public static void main(String[] args) {
        Integer[] c = {8,4,5,7,1,3,6,2};
        System.out.println("排序前：" + Arrays.toString(c));
        sort(c);
        System.out.println("排序后：" + Arrays.toString(c));
    }
}

排序前：[8, 4, 5, 7, 1, 3, 6, 2]
排序后：[1, 2, 3, 4, 5, 6, 7, 8]

  • 时间复杂度分析

    归并排序是 分治思想 的最典型的例子，上面的算法中，对a[lo…hi]进行排序，先将它分为a[lo…mid]和
    a[mid+1…hi]两部分，分别通过递归调用将他们单独排序，最后将有序的子数组归并为最终的排序结果。该递归的出口在于如果一个数组不能再被分为两个子数组，那么就会执行merge进行归并，在归并的时候判断元素的大小进行排序

用树状图来描述归并，如果一个数组有8个元素，那么它将每次除以2找最小的子数组，共拆log8次，值为3，所以树共有3层，那么自顶向下第k层有2^k 个子数组，每个数组的长度为2^ (3-k)，归并最多需要2^(3-k)次比较。因此每层的比较次数为 2^k * 2^(3-k) = 2^3，那么3层总共为 3 * 2^3

假设元素的个数为n，那么使用归并排序拆分的次数为log2(n)，所以共log2(n)层，那么使用log2(n)替换上面3 * 2^3中的3这个层数，最终得出的归并排序的时间复杂度为：log2(n) * 2^(log2(n)) = log2(n) * n

根据大O推导法则，忽略底数，最终归并排序的时间复杂度为：O(n*logn) （对数阶）

  • 缺点

    需要申请额外的数组空间，导致空间复杂度提升，是典型的 以空间换时间 的操作

  • 归并排序与希尔排序性能测试

public class SortTest {
    /**
     * 比较希尔排序和归并排序
     */
    @Test
    public void testMergeAndShell(){
        Integer[] c = getArray(10_0000);
        long start = System.currentTimeMillis();
        //ShellSort.sort(c);//用时：23
        MergeSort.sort(c);//用时：52
        long end = System.currentTimeMillis();
        System.out.println("用时：" + (end - start));
    }

    /**
     * 得到待排序数组
     * 最坏情况（倒序，从大到小）
     *
     * @param n
     * @return
     */
    private Integer[] getArray(int n) {
        Integer[] c = new Integer[n];
        for (int i = 0; i < n; i++) {
            c[i] = n - i;
        }
        return c;
    }
}

通过测试，发现希尔排序和归并排序在处理大批量数据时差别不是很大

4.3、快速排序

快速排序是 对冒泡排序的一种改进。它的基本思想是：通过一 趟排序将要排序的数据分割成独立的两部分，其中一部分的所 有数据都比另外一部分的所有数据都要小，然后再按此方法 对这两部分数据分别进行快速排序，整个排序 过程可以递归进行，以此达到整个数据变成有序序列

案例：

  • 需求： 排序前:{6, 1, 2, 7, 9, 3, 4, 5, 8} 排序后:{1, 2, 3, 4, 5, 6, 7, 8, 9}

  • 排序原理

    1. 首先设定一个 分界值，通过该分界值将数组分成左右两部分

    2. 将大于或等于分界值的数据放到到数组右边，小于分界值的数据放到数组的左边。此时左边部分中各元素都小于或等于分界值，而右边部分中各元素都大于或等于分界值

    3. 然后，左边和右边的数据可以独立排序。对于左侧的数组数据，又可以取一个分界值，将该部分数据分成左右两部分，同样在左边放置较小值，右边放置较大值。右侧的数组数据也可以做类似处理

    4. 重复上述过程，可以看出，这是一个递归定义。通过递归将左侧部分排好序后，再递归排好右侧部分的顺序。当左侧和右侧两个部分的数据排完序后，整个数组的排序也就完成了

  • API设计

  • 切分原理
    把一个数组切分成两个子数组的基本思想：
    1. 找一个基准值，用两个指针分别指向数组的头部和尾部
    2. 先从尾部向头部开始搜索一个比基准值小的元素，搜索到即停止，并记录指针的位置
    3. 再从头部向尾部开始搜索一个比基准值大的元素，搜索到即停止，并记录指针的位置
    4. 交换当前左边指针位置和右边指针位置的元素
    5. 重复2,3,4步骤，直到左边指针的值大于右边指针的值停止

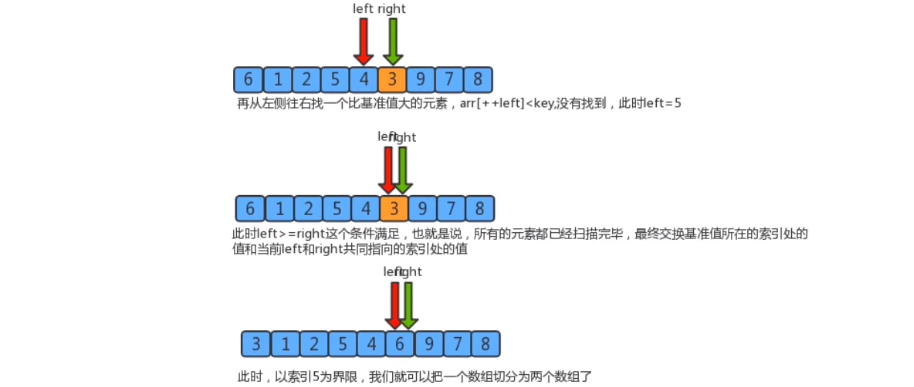
  • 代码实现
import java.util.Arrays;

/**
 * @author 土味儿
 * Date 2021/10/5
 * @version 1.0
 * 快速排序
 * 冒泡排序的优化；递归；双指针
 */
public class Quick {
    /**
     * 比较次数
     */
    private static int l_num;
    /**
     * 交换次数
     */
    private static int e_num;

    /**
     * 排序
     *
     * @param c 目标数组
     */
    public static void sort(Comparable[] c) {
        int i = 0;
        int j = c.length - 1;
        sort(c, i, j);
    }

    /**
     * 对数组c中从位置i到j处的元素进行排序
     *
     * @param c 目标数组
     * @param i 起始索引
     * @param j 终止索引
     */
    private static void sort(Comparable[] c, int i, int j) {
        // 【1】参数有效性检查；分组判断条件：j<=i时，不能再分组
        if (j <= i) {
            return;
        }

        // 【2】分组
        int m = partition(c, i, j);

        // 【3】分组后递归排序
        // m处的元素为临界值，左边小，右边大，不需要再排序，所以是 (i,m-1)，(m+1,j)
        sort(c, i, m - 1);
        sort(c, m + 1, j);
    }

    /**
     * 分组【核心方法】
     * 对数组c中从位置i到j处的元素，分组排序，i处元素作为临界值
     * 用双指针分别从前后查找，排序后小于临界值的都在左边，大于的在右边     *
     *
     * @param c 目标数组
     * @param i 起始索引
     * @param j 终止索引
     * @return 临界值的索引位置
     */
    private static int partition(Comparable[] c, int i, int j) {
        // 【1】临界值：默认第一个元索
        Comparable value = c[i];

        // 【2】定义左右指针；分别指向待切分数组的最小索引处和最大索引处的下一处
        int l = i;
        int r = j + 1;

        // 【3】切分
        while (true) {
            // 右指针r从右向左依次比较，找到一个比临界值小的就停止
            while (less(value, c[--r])) {
                // 如果从右向左，一直到临界值，都没有找到一个更小的值，说明临界值右边的都比临界值大，就退出循环
                if (r <= i) {
                    break;
                }
            }
            // 左指针l从左向右依次比较，找到一个比临界值大的就停止
            while (r > l && less(c[++l], value)) {
                // 如果从左向右，一直到最后，都没有找到一个更大的值，说明临界值右边的都比临界值小，就退出循环
                if (l >= j) {
                    break;
                }
            }
            // 比较左右指针
            if (r > l) {
                exch(c, l, r);
            } else {
                break;
            }
        }

        // 【4】交换临界值
        if (r > i) {
            exch(c, i, r);
        }

        // 【5】返回临界值索引
        return r;
    }

    /**
     * 判断元素v是否小于w
     *
     * @param v 目标元素
     * @param w 目标元素
     * @return
     */
    private static boolean less(Comparable v, Comparable w) {
        l_num++;
        return v.compareTo(w) < 0;
    }

    /**
     * 交换数组c中位置i和j处的元素
     *
     * @param c 目标数组
     * @param i 交换索引
     * @param j 交换索引
     */
    private static void exch(Comparable[] c, int i, int j) {
        if (c[i] != c[j]) {
            e_num++;
            Comparable temp = c[i];
            c[i] = c[j];
            c[j] = temp;
        }
    }

    public static void main(String[] args) {
        //Integer[] c = {9, 4, 7, 6, 4, 3, 2, 1};
        //5 | 3 1 2 | 9 7 8 9 | 4 6 3
        Integer[] c = {5, 3, 1, 2, 9, 7, 8, 9, 4, 6, 3};
        //Integer[] c = {1, 2, 3, 4, 5, 6, 7, 8, 9};
        System.out.println("排序前：" + Arrays.toString(c));
        sort(c);
        System.out.println("排序后：" + Arrays.toString(c));

        System.out.println("比较次数：" + l_num);
        System.out.println("交换次数：" + e_num);
    }
}

排序前：[5, 3, 1, 2, 9, 7, 8, 9, 4, 6, 3]
排序后：[1, 2, 3, 3, 4, 5, 6, 7, 8, 9, 9]
比较次数：31
交换次数：9

  • 快速排序和归并排序的区别

    • 快速排序是另外一种分治的排序算法，它将一个数组分成两个子数组，将两部分独立的排序

    • 快速排序和归并排序是互补的：

      归并排序将数组分成两个子数组分别排序，并将有序的子数组归并从而将整个数组排序，而快速排序的方式则是当两个数组都有序时，整个数组自然就有序了。在归并排序中，一个数组被等分为两半，归并调用发生在处理整个数组之前

      在快速排序中，切分数组的位置取决于数组的内容，递归调用发生在处理整个数组之后

  • 时间复杂度分析

    快速排序的一次切分从两头开始交替搜索，直到left和right 重合，因此，一次切分算法的时间复杂度为O(n)，但整个快速排序的时间复杂度和切分的次数相关。

    最优情况：每一次切分选择的基准数字刚好将当前序列等分。

如果我们把数组的切分看做是一个树，那么上图就是它的最优情况的图示，共切分了logn次

所以，最优情况下，快速排序的时间复杂度为：O(n*logn) 对数阶

最坏情况：每一次切分选择的基准数字是当前序列中最大数或者最小数，这使得每次切分都会有一个子组，那么总
共就得切分n次，所以，最坏情况下，快速排序的时间复杂度为：O(n^2) 平方阶

平均情况：每一次切分选择的基准数字不是最大值和最小值， 也不是中值，这种情况我们也可以用数学归纳法证 明，快速排序的平均时间复杂度为：O(n*logn) （对数阶）

4.4、排序的稳定性

  • 定义

    数组arr中有若干元素，其中A元素和B元素相等，并且A元素在B元素前面，如果使用某种排序算法排序后，能够保证 A元素依然在B元素的前面，可以说这个该算法是稳定的

    简而言之：相等元素排序后，前后位置不变，即稳定

  • 稳定性的意义

    • 如果一组数据只需要一次排序，则稳定性一般是没有意义的

    • 如果一组数据需要多次排序，稳定性是有意义的

      例如：

      要排序的内容是一组商品对象，第一次排序按照价格由低到高排序，第二次排序按照销量由高到低排序，如果第二次排序使用稳定性算法，就可以使得相同销量的对象依旧保持着价格高低的顺序展现，只有销量不同的对象才需要重新排序。这样既可以保持第一次排序的原有意义，且可以减少系统开销

      第一次按照价格从低到高排序：

第二次按照销量进行从高到低排序：

4.5、比较

排序算法特点稳定性时间复杂度性能推荐
冒泡排序大的放后面稳定O(N^2) (平方阶)低小数据量
选择排序小的放前面不稳定O(N^2) （平方阶）低小数据量
插入排序插入到合适位置稳定O(N^2) （平方阶）低小数据量
希尔排序按增长量分组不稳定-高大数据量；单次查询推荐用
归并排序先等分，后合并
辅助数组；三指针		稳定O(n*logn) （对数阶）高大数据量；多次查询推荐用
快速排序基准值；双指针不稳定O(n*logn) （对数阶）高大数据量（可能栈溢出）

  • 冒泡排序

    • 稳定

      只有当arr[i] > arr[i+1]的时候，才会交换元素的位置，而相等的时候并不交换位置

    • 原理

      从前向后，一遍一遍，两两比较，每一遍都使最大的放在后面

  • 选择排序

    • 不稳定

      给每个位置选择当前元素最小的；例如有数据 {5(1)，8 ，5(2)， 2， 9 }，第一遍选择到的最小元素为2，所以5(1)会和5(2)进行交换位置，此时5(1)到了5(2)后面， 破坏了稳定性

    • 原理

      从前向后，一遍一遍，两两比较，每一遍都找出最小的放在前面

  • 插入排序

    • 稳定

      比较是从有序序列的末尾开始，也就是想要插入的元素和已经有序的最大者开始比较，如果比它大则直接插入在其后面，否则一直往前找直到找到它该插入的位置。如果碰见一个和插入元素相等的，那么把要插入的元素放在相等元素的后面。所以，相等元素的前后顺序没有改变，从原无序序列出去的顺序就是排好序后的顺序

    • 原理

      把数组分为有序、无序两组，从无序组中取第一个，插入到有序中合适的位置，直至无序组为空

  • 希尔排序

    • 不稳定

      按照不同步长对元素进行插入排序，虽然一次插入排序是稳定的，不会改变相同元素的相对顺序，但在不同的插入排序过程中，相同的元素可能在各自的插入排序中移动，最后其稳定性就会被打乱

  • 归并排序

    • 稳定

      在归并的过程中，只有arr[i]<arr[i+1]的时候才会交换位置，如果两个元素相等则不会交换位置，所以并不会破坏稳定性

  • 快速排序

    • 不稳定

      把第一个当作基准值，从右向左找一个比基准值小的元素，从左向右找一个比基准值大的元 素，然后交换这两个元素，此时会破坏稳定性

评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包

打赏作者

土味儿~

你的鼓励将是我创作的最大动力

¥1 ¥2 ¥4 ¥6 ¥10 ¥20
扫码支付：¥1
获取中
扫码支付

您的余额不足，请更换扫码支付或充值

打赏作者

实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值