多分类混淆矩阵TPTNFN

最新推荐文章于 2024-06-07 17:39:41 发布
原创 最新推荐文章于 2024-06-07 17:39:41 发布 · 1k 阅读 · 0 ·
CC 4.0 BY-SA版权
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
文章标签：

#机器学习 #人工智能

博客探讨了多分类混淆矩阵的正确构建方法，指出了一种常见错误的理解，即每个类别独立计算准确率。文中通过示例解释了混淆矩阵相对于某一特定类别的正确表示，并讨论了其对评估分类模型性能的重要性。

本来是想找一下多分类的混淆矩阵说明
但是发现网上的都是二分类，下面这种
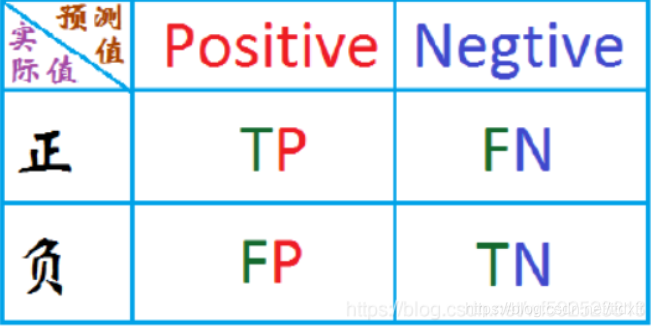
图转自博主
二分类的图转自博主，下面放上链接
https://blog.youkuaiyun.com/wf592523813/article/details/95202448
用自己的理解画了个多分类的混淆矩阵的表不知道对不对
和大家分享一下
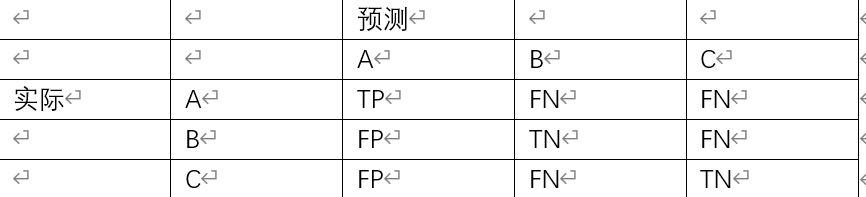
在这里插入图片描述
后来问了一下明白人，发现我这个不对TN不是这样归类的
因为如果按我这个来的话每一类分别算的准确率Acc都是一样的
应该是这样，为了简单举例
下面这个图是相对于B类而言的在这里插入图片描述

混淆矩阵与多分类混淆矩阵概念详解及其应用求 Precision F1-Score Recall
专注于图像领域，主要研究内容包括计算机视觉和深度学习，特别是在图像分类、目标检测和图像生成等方面有深入的研究和实践经验。
05-21 2597
混淆矩阵，顾名思义，是一个由数字组成的矩阵，它告诉我们模型在哪些地方会出现混淆。它是分类模型预测性能的类别分布，也就是说，混淆矩阵是将预测结果映射到数据所属原始类别的一种有组织的方式。这也意味着，只有在已知输出分布的情况下，即在监督学习框架中，才能使用混淆矩阵。混淆矩阵不仅可以计算分类器的准确度（无论是全局准确度还是分类准确度），还有助于计算开发人员通常用来评估模型的其他重要指标。
分类模型评估利器-混淆矩阵
M姐实验室
12-30 1036
混淆矩阵（Confusion Matrix）是机器学习领域中用于评估分类模型性能的一种工具。FLUS工具三篇文章（之一）
多分类问题的混淆矩阵
weixin_44677208的博客
10-14 2985
混淆矩阵、查准率和召回率 夏令营时候遇到过混淆矩阵、查准率和召回率的问题，今天看书又回顾到这个问题，个人觉得对这个概念还是需要有非常清醒的认识的，做个记录。 混淆矩阵 假设正例为我有病，那反例就是我没病。 TP就是，我有病，判断有病。 FN就是，我有病，但是没判断出来，觉得我没病。 FP是，我没病，但是判断我有病。 TN是，我没病，判断的也是我没病，判断的是正确的。 真实情况\预测结果 正例 反例 正例 TP FN 反例 FP TN 查准率P和召回率R P=TPTP+FPP=\fra
多类分类器的混淆矩阵_使用混淆矩阵调试分类器
weixin_26750481的博客
09-16 2740
多类分类器的混淆矩阵 介绍 (Introduction) A confusion matrix is a visual way to inspect the performance of a classification model. Metrics such as accuracy can be inadequate in cases where there are large class im...
多分类任务的混淆矩阵处理
JustKian的博客
09-26 1万+
多分类任务的混淆矩阵处理 在多分类任务中，不适合使用PR曲线和ROC曲线来进行指标评价，但我们仍可以通过混淆矩阵来进行处理。可以通过matplotlib的matshow()函数，直观地展示分类结果的好坏。 先使用cross_val_predict得出各个分类值的分数 y_train_pred = cross_val_predict(sgd_clf, X_train_scaled, y_train...
多分类任务的混淆矩阵
deephub
01-12 8269
今天我将讨论如何在多分类中使用混淆矩阵评估模型的性能。 什么是混淆矩阵？ 它显示了实际值和预测值之间的差异。 它告诉我们有多少数据点被正确预测，哪些数据点没有被正确预测。对于多分类来说，它是一个 N * N 矩阵，其中 n 是编号。 输出列中的类别，也称为目标属性。一二分类任务中包含了 2 个类也就是一个 2*2 矩阵，一般情况下介绍混淆矩阵都会以二分类为例。 如果有 3 个类呢？那么将得到一个 3*3 矩阵依此类推。 通过上面描述我们知道，混淆矩阵的类将具有相同数量的行和列。 下面让我们尝试了解一些常用术
多分类混淆矩阵详解
weixin_37522117的博客
06-07 3468
多分类混淆矩阵详解及代码示例
深度学习自学记录（3）——两种多分类混淆矩阵的Python实现（含代码）
12-21
在深度学习领域，混淆矩阵是评估分类模型性能的重要工具，特别是在多分类问题中。混淆矩阵是一种二维表格，展示了模型预测结果与实际结果的对比，帮助我们理解模型在不同类别上的表现。它由True Positive (TP)，True...
confusion matrix为使用MATLAB绘制多分类的混淆矩阵图
08-06
confusion matrix使用MATLAB绘制多分类的混淆矩阵图，可自定义横纵坐标、字体、渐变颜色等，适用于深度学习、机器学习中多分类任务的结果分析混淆矩阵图。
confusion_混淆矩阵、pytorch、模型_混淆矩阵pytorch_混淆矩阵_
10-04
在机器学习领域，模型的评估是至关重要的，而混淆矩阵是一种常用的评估工具，尤其是在二分类或多分类问题中。本文将深入探讨混淆矩阵的概念，以及如何在PyTorch框架下使用它来评估深度学习模型。 首先，混淆矩阵...
多分类问题中混淆矩阵(Confusion Matrix)的Matlab画法
12-07
Matlab code for computing and visualization: Confusion Matrix, Precision/Recall, ROC, Accuracy, F-Measure etc. for Classification. Matlab通过分类的label计算混淆矩阵Confusion Matrix并且显示的函数只要一句代码就行了，方便。 [confusion_matrix]=compute_confusion_matrix(predict_label,num_in_class,name_class);
多分类混淆矩阵（sklearn.metrics）
sinat_38059712的博客
01-31 3376
转载自：苏格拉- PYTHON - OPENCV实现图像超像素分割（SLIC、SEEDS、LSC） sklearn.metrics.multilabel_confusion_matrix(y_true, y_pred, *, sample_weight=None, labels=None, samplewise=False) Examples Multilabel-indicator case: >>> import numpy as np >>> from s..
多分类混淆矩阵的理解
这个人很蓝
08-08 1万+
借用其它博客的一张例子示意图，该图为一个三分类问题的混淆矩阵，对角线的值表示分类器对该类别预测正确的个数，每一列纵轴表示这个类别真实的样本数，例如从第一列可以得知猫一共有10+3+5=18只，因此总样本数为三列之和，即66。 下面以猫为例，介绍从混淆矩阵中计算TP、TN、FP、FN。 TP(True Positive)和FN(False Negative)：从第一列可知，猫一共有18只，其中只有10个被分类器正确预测，而有3只被预测成狗，5只被预测成猪，因此对猫这个类别来说，TP=10（正确预测成猫的样本
机器学习（)-多分类任务混淆矩阵
TIAN妹的博客
12-28 1万+
混淆矩阵的实例 当分类问题是二分问题是，混淆矩阵可以用上面的方法计算。当分类的结果多于两种的时候，混淆矩阵同时适用。 一下面的混淆矩阵为例，我们的模型目的是为了预测样本是什么动物，这是我们的结果： 通过混淆矩阵，我们可以得到如下结论： Accuracy 在总共66个动物中，我们一共预测对了10 + 15 + 20=45个样本，所以准确率（Accuracy）=45/66 = 68.2%...
多分类中混淆矩阵的TP,TN,FN,FP计算
m0_62919535的博客
09-16 7941
创建混淆矩阵# 寻找GT中为目标的像素索引# 统计像素真实类别t[k]被预测成类别p[k]的个数@property"""计算混淆矩阵的TN, FP, FN, TP"""if n == 2:if n > 2:"""主要在eval的时候使用,你可以调用ravel获得TN, FP, FN, TP, 进行其他指标的计算计算全局预测准确率(混淆矩阵的对角线为预测正确的个数)计算每个类别的准确率计算每个类别预测与真实目标的iou,IoU = TP / (TP + FP + FN)"""
深入了解多分类混淆矩阵：解读、应用与实例
null18的博客
09-28 4449
混淆矩阵是一个用于可视化分类模型性能的表格，它将模型的预测结果与实际标签进行比较。对于多分类问题，混淆矩阵的结构可能会略有不同，但基本思想相同。其中，每一行代表实际类别，每一列代表模型的预测类别。矩阵的对角线上的元素（TPii）表示模型正确预测的样本数，而非对角线元素则表示模型错误预测的样本数。解读混淆矩阵True Positives (TP)：模型正确预测为第 i 类的样本数。False Positives (FP)：模型错误地预测为第 i 类的样本数。
多分类混淆矩阵：数据挖掘与模型评估
AI天才研究院
12-23 1287
1.背景介绍 数据挖掘是指从大量数据中发现有价值的信息和知识的过程。在数据挖掘中，我们通常需要对数据进行预处理、清洗、转换等操作，以便于后续的分析和模型构建。模型评估是数据挖掘过程中的一个关键环节，它旨在评估模型的性能和准确性。 在多分类问题中，数据样本可能属于多个类别之一。为了评估模型的性能，我们需要一个能够有效地表示模型在多分类问题上的表现的指标。混淆矩阵就是一种常用的评估指标，它可以帮助...
67-多分类问题中的混淆矩阵
qq_41033011的博客
10-21 635
多分类问题中的混淆矩阵    具体代码见 67 多分类问题中的混淆矩阵.ipynb
【机器学习笔记15】多分类混淆矩阵、F1-score指标详解与代码实现（含数据）
热门推荐
issey的博客
11-01 2万+
混淆矩阵简介;二分类混淆矩阵;多分类混淆矩阵;准确率、精确率、召回率、特异度；F1-score；示例与代码实现；使用sklearn对比计算结果是否正确
多分类混淆矩阵定义
最新发布
03-18
### 多分类混淆矩阵的定义 在机器学习中，多分类混淆矩阵是一个 n×n 的表格，其中 n 表示类别的总数。每一行代表真实标签的实际分布，而每一列则表示预测标签的结果分布[^3]。具体来说： - **第 i 行 j 列** 的值表示被错误地预测为类别 j 的实际属于类别 i 的样本数。 - 对角线上的元素 \( C_{ii} \) 表示正确预测为类别 i 的样本数。 通过这个矩阵，我们可以评估模型的表现，尤其是识别不同类别时的能力。 ### 多分类混淆矩阵的计算方法 假设有一个三分类问题，其真实的类别标签集合为 {0, 1, 2}，对应的混淆矩阵可以写成如下形式： \[ C = \begin{bmatrix} C_{00} & C_{01} & C_{02}\\ C_{10} & C_{11} & C_{12}\\ C_{20} & C_{21} & C_{22} \end{bmatrix} \] #### 步骤说明 为了构建上述混淆矩阵，我们需要遍历测试集中的每个样本，并记录以下信息： - 如果某个样本的真实标签是类别 i 并且被预测为类别 j，则增加 \( C_{ij} \) 的计数值。 最终得到的矩阵可以帮助我们进一步计算各种性能指标，比如精确率（Precision）、召回率（Recall）和 F1 分数等[^4]。 当需要针对某特定类别 k 来计算 Precision 和 Recall 时，可以通过将该类别视为唯一的正例，其余所有类别合并作为负例的方式来进行处理[^1]。此时，原始的 n×n 混淆矩阵会被简化为一个 2×2 的二分类混淆矩阵。 以下是 Python 中创建并显示混淆矩阵的一个简单例子： ```python from sklearn.metrics import confusion_matrix import numpy as np # Example true and predicted labels for a multi-class problem with three classes. y_true = [2, 0, 2, 2, 0, 1] y_pred = [0, 0, 2, 2, 0, 2] cm = confusion_matrix(y_true, y_pred) print("Confusion Matrix:") print(cm) ``` 此代码片段利用 `sklearn` 库生成了一个基于给定真值列表 (`y_true`) 及预测值列表 (`y_pred`) 的混淆矩阵。
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值