二分归并排序求逆序对

最新推荐文章于 2025-10-12 10:47:35 发布

原创最新推荐文章于 2025-10-12 10:47:35 发布 · 736 阅读

CC 4.0 BY-SA版权

题目：The Number of Inversions

题面：

For a given sequence , the number of pairs where and , is called the number of inversions. The number of inversions is equal to the number of swaps of Bubble Sort defined in the following program:

bubbleSort(A)
  cnt = 0 // the number of inversions
  for i = 0 to A.length-1
    for j = A.length-1 downto i+1
      if A[j] < A[j-1]
	swap(A[j], A[j-1])
	cnt++

  return cnt

For the given sequence , print the number of inversions of . Note that you should not use the above program, which brings Time Limit Exceeded.

Input

In the first line, an integer , the number of elements in , is given. In the second line, the elements () are given separated by space characters.

output

Print the number of inversions in a line.

Constraints

are all different

Sample Input 1

5
3 5 2 1 4

Sample Output 1

Sample Input 2

3
3 1 2

Sample Output 2

题解：

递归回溯是个奇妙的东西，几乎很多难题都要用到递归和回溯，能解出更多的解法，也能将所有情况都考虑到

逆序对，如果存在正整数 i, j 使得 1 ≤ i < j ≤ n 而且 A[i] > A[j]，则 <A[i], A[j]> 这个有序对称为 A 的一个逆序对，也称作逆序数。

例如，数组（3，1，4，5，2）的逆序对有(3,1),(3,2),(4,2),(5,2)，共4个，数据在数组中的位置是左边，但是数值比右边的某些数据大，这两个就组成了一个逆序对。

求解逆序对方法：

1.最原始的冒泡法

#include<stdio.h>
#include<iostream>
#include<string.h>
using namespace std;
typedef long long ll;
#include<stdio.h>
int b[10];
int main()
{
	int num,i,j,k=0;
	scanf("%d",&num);
	for(i=0;i<num;i++)
		scanf("%d",&b[i]);
	for(i=0;i<num-1;i++)
		for(j=0;j<num-1-i;j++)
			{
				if(b[j]>b[j+1])
				{
				swap(b[j],b[j+1]);
					k++;
				}
			}
	printf("%d",k);
	
	return 0;
}

时间复杂度是O(n^2) 数据大的时候，就会超时。这个方法是很容易理解的，我就不做解释了，c语言的书上有相关的解释，这个还是很简单的，但不是最优的解法。

2.二分并归排序求解逆序对

我一开始也是众多迷茫读者中的一个，因为网上的题解都是些图解（不是图解不好），但是对于ACM新手来说，由图解就上手敲代码，还是很困难的（要经过很长的时间和大量的题的磨练才能够到达的）。

首先它是递归回溯与二分的一个结合，任何其中的一个都是比较难实现的，这里我们先将递归回溯和二分分开来考虑，因为这里面有很多的状态跳转，很不好理解。

第一先知道二分是怎么分的，看图解

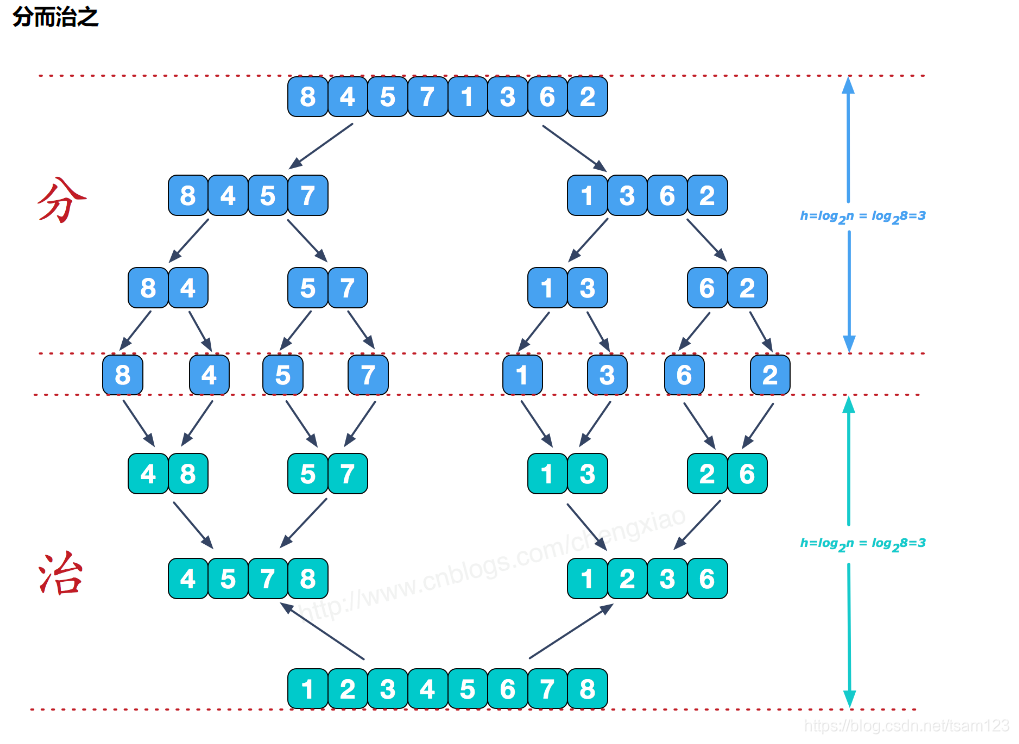
https://visualgo.net/zh 这是一个模拟排序的动画，大家可以看看，应该是很有帮助的。分区间（是由递归）和合并区间（是由一个辅助数组来实现的）。

代码实现有些注释已经附上：

#include<stdio.h>
#include<iostream>
#include<string.h>
using namespace std;
typedef long long ll;
const ll maxn=200005;
ll a[maxn],b[maxn];
ll count;

void merge_sort1(ll x,ll mid,ll y)
{
	//以下 是 将左右部分比较，谁小 就将谁装进b数组（辅助数组），这样就保证b中 是有序的。  
	ll i=x,j=mid+1,k=x;
		while(i<=mid&&j<=y)
		{
			if(a[i]<=a[j])
				b[k++]=a[i++];       //如果左边区间的某个元素小于右半边的元素，就不用考虑逆序对，因为这不是逆序对，就将左边区间元素下标+1，再比。 
			else
				{
					b[k++]=a[j++];
					count+=mid-i+1;   //在比较两边的区间 元素时，mid 两边的 区间 全是有序的，mid - i + 1 就是 中间 mid点（也包括mid 处点的元素） 到比较的左点 之间有几个元素，因为左边（右边）全是有序的，之间有几个元素，那就有几个比右半边元素大的逆序对。然后右半边的元素下标+1，再比. 
				}	
		}
		
		
		
	// 以下的部分 就是 两边的东西谁比较大，就将大的装进b数组 （辅助数组）。 
	while(i<=mid)						
		b[k++]=a[i++];
	while(j<=y)
		b[k++]=a[j++];	
	// 再把b数组 中的东西  从x 到 y b数组中已经有序的东西，复制进 a 数组。	
	for(i=x;i<=y;i++)
		a[i]=b[i];
			
			
			
			
	//经过以上两个 部分 ，就将 从 x 到 y 的部分 排好序了。 
}


void merge_sort(ll x,ll y)
{
	if(x==y)              //递归分区间，结束标志
		return ;
	ll mid=(x+y)/2;       //每次取半 
	merge_sort(x,mid);    // 先排左边（不是一开始到这里就排，而是要回溯时，用 merge_sort1(x,mid,y)去排） ，这里是可以分区间，分出左边以两个为一组的区间。 
	merge_sort(mid+1,y);  // 再排右边（不是一开始到这里就排，而是要回溯时，用 merge_sort1(x,mid,y)去排） ，这里也是分区间的，分出右边以两个为一组的区间。 
	merge_sort1(x,mid,y); // 这部好了的话，就是（左或者右的一半） 已经排好了，进行下一半的排序。 
	
	//递归： 先递归找到最小的区间（有两个组成的）。
	//回溯： 由小的区间 到大的区间，去排左右两边的区间 里的元素。 
	
}


int main()
{
	ll num;
	ll i;
	scanf("%lld",&num);
	for(i=0;i<num;i++)
		scanf("%lld",&a[i]);
	merge_sort(0,num-1); 
	printf("%lld\n",count);
	return 0;
}

如何分区间，是个重要的部分，这才能保证，怎么说呢，你才不会有BUG，不会出错。

看了上面的代码，我们先来弄懂它是怎么用代码实现分区间的。

mid=(x+y)/2 , 这个x(一个区间的起始) 和y（一个区间的结束）和 mid 都是数组中的下标，不是数组的长度，就如 5 4 1 3 起始x位置 0 ，y位置 3 , mid = (x+y)/2=1 分区间， mid=1处 , x=0 , y=3; 这时想想，什么时候还能再分？，当x 和 mid 相等的时候，就相当于x位置处的数据和mid 位置处的数据相同，这时，就不能再分出来，这其实上就用了递归了。我们已经分好左半边的了，如何分右边的？方法一样用 x=mid+1 , 和 y=区间的结束位置。不断mid=(x+y)/2,当 mid 与 x 相等的时候，就不能再分区间了。

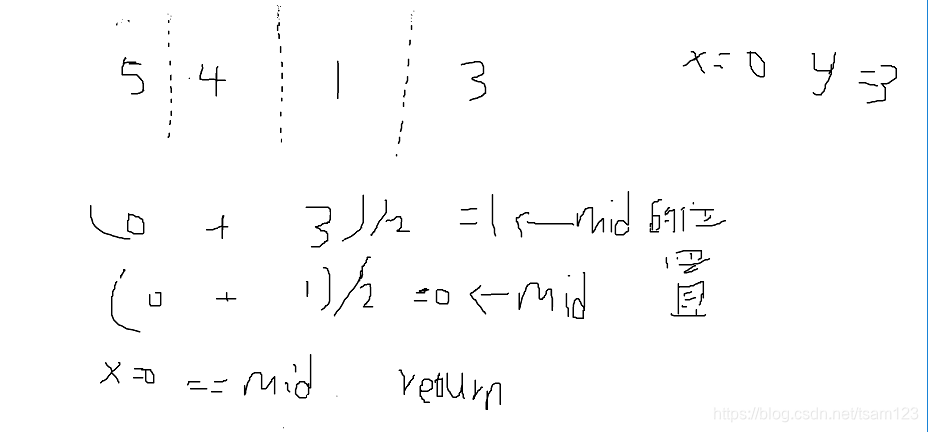
分完区间后，就要考虑到如何排序，通过比较来找逆序对，这个过程是包含在分区间中的，它是一边分区间，一边比较排序的，不是一个个独立的过程，递归分区间，回溯时，就可以去排序，找逆序对。

下面看看如何来求逆序对和排序。

先附上图解：

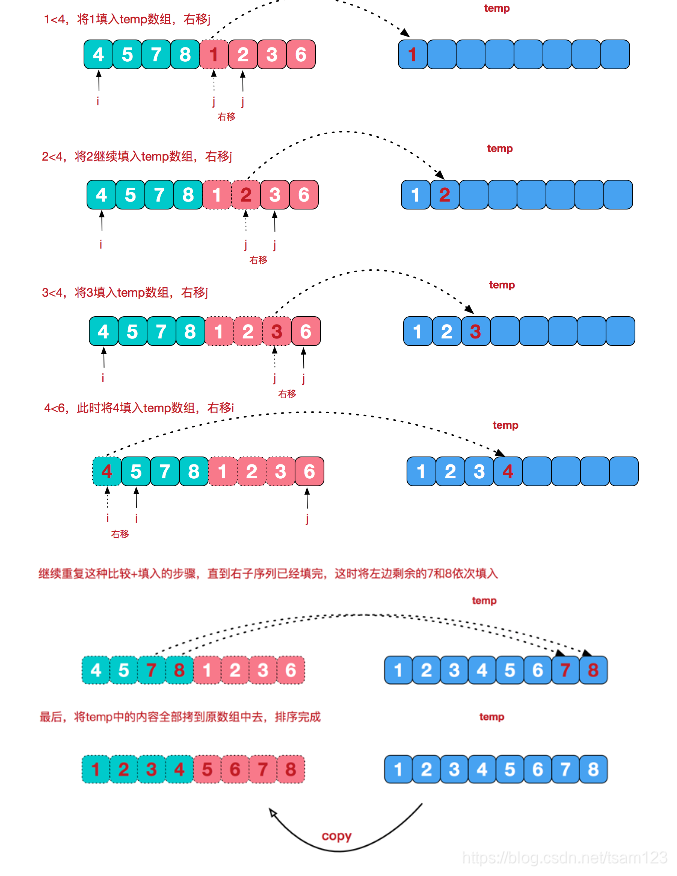
这个图解是每次回溯是都会这样排。下面看看代码实现

void merge_sort1(ll x,ll mid,ll y)
{
	//以下 是 将左右部分比较，谁小 就将谁装进b数组（辅助数组），这样就保证b中 是有序的。  
	ll i=x,j=mid+1,k=x;
		while(i<=mid&&j<=y)
		{
			if(a[i]<=a[j])
				b[k++]=a[i++];       //如果左边区间的某个元素小于右半边的元素，就不用考虑逆序对，因为这不是逆序对，就将左边区间元素下标+1，再比。 
			else
				{
					b[k++]=a[j++];
					count+=mid-i+1;   //在比较两边的区间 元素时，mid 两边的 区间 全是有序的，mid - i + 1 就是 中间 mid点（也包括mid 处点的元素） 到比较的左点 之间有几个元素，因为左边（右边）全是有序的，之间有几个元素，那就有几个比右半边元素大的逆序对。然后右半边的元素下标+1，再比. 
				}	
		}
		
		
		
	// 以下的部分 就是 两边的东西谁比较大，就将大的装进b数组 （辅助数组）。 
	while(i<=mid)						
		b[k++]=a[i++];
	while(j<=y)
		b[k++]=a[j++];	
	// 再把b数组 中的东西  从x 到 y b数组中已经有序的东西，复制进 a 数组。	
	for(i=x;i<=y;i++)
		a[i]=b[i];
			
			
			
			
	//经过以上两个 部分 ，就将 从 x 到 mid+1 的部分 排好序了。 
}

在这里，我们需要一个辅助数组来辅助，每次排好，都需要往原来的数组里复制一下，在这里，我们需要很多的下标变量来往辅助数组里面装东西，由上图可知，我们需要分别比较两边区间（都是已经排好序的）各个位数据的大小，则就要三个 i , j , k ，来分别匹配左半边区间的开始位置，右半边区间的开始位置，左区间的开始位置，如果左半边的元素小于右半边的对应元素，则就把左半边这个元素装进辅助数组中，否则就把右半边的这个元素装进辅助元素中，当装的时候，相应的下表变量也会变化，当i和j都小于相应的（mid）和（y）时，就继续比较来排序，当其中一个不满足时，就不在比了（因为都是有序的）。这时辅助数组中的值都是有序的，并且都是两边区间比较小的，两边区间有一个的i或者j已经大于mid或者y。这时该往辅助数组里面排剩下区间的元素，如果i<=mid 就把左半边区间（剩下的）的元素装到辅助数组里面（装的时候辅助数组肯定是有序的），如果j<=y(又区间的结束)时，就装它剩下的元素，为什么就能精确的装那个数据呢？因为有下标变量i,j,k(是辅助数组的下标)来控制。

这样就能使辅助数组中是有序的，然后再将辅助数组的有序元素，一个一个都装到原来数组中，这样就保证有序了。

以上的过程都是每次回溯时要做的，每次排的时候都会上演一次，不只是最后一次排的。

先用递归分区间在这之后用一个合并的函数，而这就是用递归一步一步分和分和实现的。

接下来，怎么来求逆序对，上面已经有了定义了，逆序对就是下标与数据大小不同步，看一下，什么时候有逆序对

while(i<=mid&&j<=y)
		{
			if(a[i]<=a[j])
				b[k++]=a[i++];      
			else
				{
					b[k++]=a[j++];
					count+=mid-i+1;   
				}	
		}

当正常比后面区间各个数据小的时候，是没有逆序对的，当比后面区间大的时候，这时就会有了逆序对，而计数器count=mid-i+1就是这时候的逆序对的数量，由上面说的，这个 mid 就是在数组中的下标，mid - i+1 就是 mid 到 i的距离，这个距离就是此时的逆序对的个数，因为这个距离就是 mid 与 i 之间的左区间元素的个数，因为左区间是递增的，所以 x 到 mid 之间所有的点的个数就是逆序对的个数，当然下一个状态还是可能会有逆序对的，每一次和回溯，都会经过这个过程。

如果还有什么不懂的话，可以去VS 上调试几遍，弄懂。

这个时间复杂度是O(nlog^(n))；