统计学基本极限定理

oulittle

于 2019-12-06 23:12:00 发布

阅读量1.6k

点赞数

CC 4.0 BY-SA版权

分类专栏：数据挖掘文章标签：数理统计

版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。

本文链接：https://blog.youkuaiyun.com/tryhardsilently/article/details/103430801

数据挖掘专栏收录该内容

9 篇文章

订阅专栏

一、切比雪夫不等式

设随机变量X具有数学期望 $E(X)=\mu$ ，方差 $D(X)=\sigma^{2}$ , 则对任意正数 ε，不等式

$P(|X-\mu|\ge\varepsilon) \le \frac{\sigma^{2}}{\varepsilon^{2}}$

成立。

切比雪夫不等式须满足E(X)和D(X)存在且有限

切比雪夫定理大意是：

任意一个数据集中，位于其平均数m个标准差范围内的比例（或部分）总是至少为： $1-\frac{1}{m^{2}}$ ，其中m为大于1的任意正数。对于m=2，m=3和m=5有如下结果：

所有数据中，至少有3/4（或75%）的数据位于平均数2个标准差范围内

所有数据中，至少有8/9（或88.9%）的数据位于平均数3个标准差范围内

所有数据中，至少有24/25（或96%)的数据位于平均数5个标准差范围内

二、切比雪夫大数定理

设相互独立的随机变量 $X_{1},X_{2},...,X_{n},...$ 分别具有数学期望 $E(X_{1}),E(X_{2}),...,E(X_{n}),...$ 及方差 $D(X_{1}),D(X_{2}),...,D(X_{n}),...$ ，若存在常数C，使 $D(X_{i})\le C,i=1,2,...$ 则对于任意的ε>0，有

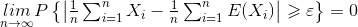
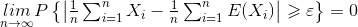
将该公式应用于抽样调查，就会有如下结论：随着样本容量n的增加，样本平均数将接近于总体平均数。从而为统计推断中依据样本平均数估计总体平均数提供了理论依据。

三、伯努利大数定律

设μ是n次独立试验中事件A发生的次数，且事件A在每次试验中发生的概率为P，则对任意正数ε，有

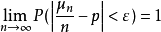
伯努利大数定律的含义是，当n足够大时，事件A出现的频率将几乎接近于其发生的概率，即频率的稳定性。伯努利大数定律是切比雪夫大数定理的特例。在实际应用中，当试验次数很大时，可以用事件的频率来代替事件的概率。

四、辛钦大数定律（弱大数定律）

设 $\left\{ x_i,i=1,2,... \right\}$ 为独立同分布的随机变量序列，若 $x_{i}$ 的数学期望存在，即对任意的ε>0，有

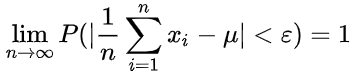
辛钦大数定律要求随机变量独立同分布，且具有相同的均值μ。切比雪夫大数定理并未要求变量 [公式] 同分布，相较于伯努利大数定律和辛钦大数定律更具一般性。

五、中心极限定理

设随机变量X1，X2，......Xn，......独立同分布，并且具有有限的数学期望和方差：E(Xi)=μ， $D_{X_{i}} = \sigma^{2}$ ,则 $\left\{ X_{n} \right\}$ 服从中心极限定理，则对任意x，有

$\lim_{n \rightarrow \infty}{P\left\{ \frac{\sum_{i=1}^{n}{X_{i}-\mu n}}{\sqrt{n}\sigma} \le x \right\}} = \frac{1}{\sqrt{2\pi}}\int_{-\infty}^{x}e^{-\frac{1}{2}t^{2}}dt=\Phi(x)$

当n很大时,随机变量

$Y_{n} = \frac{\sum_{i=1}^{n}{X_{i}-\mu n}}{\sqrt{n}\sigma}$

近似地服从标准正态分布N(0，1)。因此，当n很大时，独立同分布随机变量的和 $\sum_{i=1}^{n}{X_{i}}$ ,近似地服从正态分布 $N(n\mu,n\sigma^{2})$

六、棣莫佛－拉普拉斯定理

设随机变量X(n=1,2,...,)服从参数为n，p(0<p<1)的二项分布，则对于任意有限区间(a，b)，有

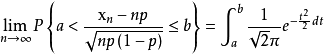
定理表明，正态分布是二项分布的极限分布，当数充分大时，我们可以利用上式来计算二项分布的概率

理解和区分大数定律与中心极限定理：

当样本足够大时，

大数定律：样本均值收敛于总体均值（期望）/ 事件出现的频率无限接近事件出现的概率
中心极限定理：样本的平均值约等于总体的平均值。不管总体是什么分布，任意一个总体的样本平均值都会围绕在总体的整体平均值周围，并且呈正态分布

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。