栈、堆、队列

最新推荐文章于 2025-07-09 19:37:28 发布

原创最新推荐文章于 2025-07-09 19:37:28 发布 · 474 阅读

2 ·

CC 4.0 BY-SA版权

数据结构专栏收录该内容

9 篇文章

订阅专栏

本文介绍了三种基本数据结构——栈、堆和队列。栈遵循后进先出（LIFO）原则，常用于递归等场景；堆是动态分配内存的数据结构，分为最大堆和最小堆；队列则是按照先进先出（FIFO）原则操作，适用于任务调度等应用。详细阐述了栈的顺序和链式存储，堆的概念和结构，以及队列的链表实现和循环队列的处理方式。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

栈

一、栈（LIFO后进先出）

栈的抽象数据类型

template <class T>
class stack
{
	virtual void clear()=0;//变为空栈
        virtual bool isEmpty()=0;//若栈空返回true
	virtual bool isFull()=0;//若栈满返回true

	virtual bool push(const T item)=0;//item入栈成功返回true
	virtual bool pop(T& item)=0;//返回栈顶内容并弹出，所以是引用T&

	virtual bool top(T& item)=0;//返回栈顶但不弹出

};

顺序存储结构

template <class T>
//顺序结构栈继承栈
class seqStack :public Stack < T >
{
private:
	int top;//栈顶指针
	int maxtop;//最大栈顶指针
	T* s;

public:
	//构造函数
	seqStack(int msize)
	{
		maxtop = msize - 1;
		s = new T[msize];
		top = -1;
	}
	//析构函数
	~seqStack()
	{
		delete[] s;
	}
};

push入栈顶

bool arrstack<T>::push(const T item)
{
	if (top == Msize - 1)//栈已满
	{
		cout << "栈满溢出" << endl;
		return false;
	}
	else
	{
		st[++top] = item;//栈顶指针加一，将新元素插入栈顶
		return true;
	}
})

pop出栈

bool arrstack<T>::pop(T& item)
{
	if (top ==  - 1)//栈为空
	{
		cout << "栈为空" << endl;
		return false;
	}
	else
	{
		item = st[top--];//返回栈顶，并所减一
		return true;
	}
})

链式栈：

template <class T>
//节点
class Node
{
private:
	T value;
	Node<T>* next;
	friend class singleStack<T>;
};

template <class T>
//顺序结构栈继承栈
class singleStack :public Stack < T >
{
private:
	Node<T>* head;

public:
	//构造函数
	singleStack()
	{
		head = new Node < T > ;
		head->next = NULL;
	}
	//析构函数
	~singleStack()
	{
		Node<T>* p;
		while (head != NULL)
		{
			p = head;
			head = head->next;
			delete(p);
		}
	}
};

压入栈顶(新节点是s)

s->data=e; s->next=s->top;

s->top=s;//新的节点s赋值给栈顶指针

template <typename T>
bool SingleStack<T>::Push(T x) {
    Node<T>* newNode = new Node<T>;
    newNode->element = x;
    newNode->next = head->next;
    head->next = newNode;
}

出栈(删除s节点)

item=s->top->data; //临时存放栈顶值

p=s->top; //节点给p

s->top=s->top->next;//栈顶指针后移一位

free（p）//释放节点p

template <typename T>
bool SingleStack<T>::Pop() {
    if (IsEmpty()) {
        cout<<"Empty"<<endl;
        return false;
    }
    Node<T>* p = head->next;
    head->next = p->next;
    delete (p);
}

注意：栈不允许“读取内部元素”，只能在栈顶操作

二、递归（栈的应用）

不断调用自己的函数，称作递归函数。

堆

堆是在程序运行时，而不是在程序编译时，申请某个大小的内存空间。即动态分配内存，对其访问和对一般内存的访问没有区别。堆是指程序运行时申请的动态内存

堆的结构，以下图为例。从根结点开始，每个结点可以有左、右两个结点，元素优先将每一层按从左到右的方式填满，即父结点最多有两个子结点，有右子结点就一定会有左子结点，同一层的某个结点左边一定是填满的。

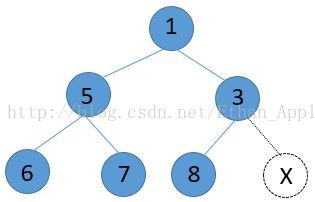
接下来，说一说堆中元素摆放的规则。堆分为两种情况，有最大堆和最小堆，最小堆就是根结点元素的值是所有元素中最小的，最大堆则相反，下图是一个最小堆。在一个摆放好元素的最小堆中，可以看到，父结点中的元素一定比子结点的元素要小，但对于左右结点的大小则没有规定谁大谁小。

详细的操作，见堆排序。

队列

1、队列（Queue）与栈一样，是一种线性存储结构，它具有如下特点：

（1）队列中的数据元素遵循“先进先出”（First In First Out）的原则，简称结构；

（2）在队尾添加元素，在队头删除元素。

2、队列的相关概念：

（1）队头与队尾：允许元素插入的一端称为队尾，允许元素删除的一端称为队头；

（2）入队：队列的插入操作；

（3）出队：队列的删除操作。

3、队列的操作：

q.empty()               如果队列为空返回true，否则返回false
q.size()                返回队列中元素的个数

q.push()                在队尾压入新元素
q.pop()                 删除队列首元素但不返回其值

q.front()               返回队首元素的值，但不删除该元素
q.back()                返回队列尾元素的值，但不删除该元素

4、队列的抽象数据类型

template<class T>
class Queue
{
	void clear();
	bool isEmpty();
	bool isFull();

	bool enQueue(const T item);//将item插入队尾，成功返回true
	bool deQueue(T& item);//返回队头元素并将其删除，成功返回true

	bool getFront(T& item);//返回队头但不删除

};

5、简单操作

#include <queue>
#include <iostream>

using namespace std;
int main()
{
	queue<int> q;
	for (int i = 0; i < 10; i++)
	{
		q.push(i);
	}
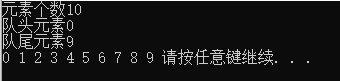
	cout << "元素个数" << q.size() << endl;
	cout << "队头元素" << q.front() << endl;
	cout << "队尾元素" << q.back() << endl;
	for (int i = 0; i < 10;i++)
	{
		int tmp = q.front();
		cout << tmp << " ";
		q.pop();
	}
	return 0;
}

6、基于链表的队列

队头指针front充当链表的表头结点，队尾指针rear指向队尾结点。

template <class T>
//节点
class Node
{
private:
	T value;
	Node<T>* next;
	friend class singleQuene<T>;
};

template <class T>
//顺序结构栈继承栈
class singleQueue :public Queue < T >
{
private:
	Node<T>* front;
	Node<T>* rear;

public:
	//构造函数
	singleQuene()
	{
		front = new Node < T > ;
		front->next = NULL;
		rear = front;
	}
	//析构函数
	~singleQuene()
	{
		Node<T>* p;
		while (head != NULL)
		{
			p = head;
			front = front->next;
			delete(p);
		}
	}
};

插入队尾

template <typename T>
bool SingleQueue<T>::Enqueue(T x) {
    Node<T>* p = new Node<T>;
    p->element = x;
    p->next = NULL;
    rear->next = p;
    rear = p;
}

删除头元素

template <typename T>
bool SingleQueue<T>::Dequeue() 
{
    if (IsEmpty()) {
        cout<<"Empty"<<endl;
        return false;
    }
    Node<T> *p = front->next;
    front->next = p->next;
    delete (p);
}

7、循环队列
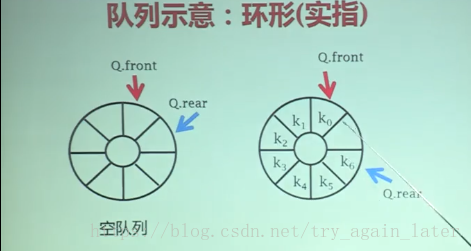。元素长度=real-front+1

指针front指向队头元素，rear指向队尾元素下一个位置。

出现“假溢出”现象————循环队列。

front与rear相差一个位置就是满。在循环队列结构下，当front==rear时为空队列，当(rear+1)%maxSize == front时为满队列。满队时实际仍有一个元素的空间未使用，这是为了与空队列的判断标准区分开。

计算队列长度公式maxsize-front;0+rear------(rear-front+maxsize)%maxsize;

顺序结构：

//队列的顺序表示,循环队列
template <typename T>
class SeqQueue :public Queue < T > 
{
private:
	int front, rear; //front指向队头元素的前一单元,rear指向队尾元素
	int maxSize;    //数组的最大长度
	T *q;
public:
	//构造函数
	SeqQueue(int mSize) 
	{
		maxSize = mSize;
		q = new T[maxSize];
		front = rear = 0;
	}
	//析构函数
	~SeqQueue() 
	{
		delete[]q;
	}
};

插入队尾

template <typename T>
bool SeqQueue<T>::Enqueue(T x) 
{
    if (IsFull()) {
        cout<<"Full"<<endl;
        return false;
    }
    rear = (rear + 1) % maxSize;
    q[rear] = x;
    return true;
}

删除头元素

template <typename T>
bool SeqQueue<T>::Dequeue()
 {
    if (IsEmpty()) {
        cout<<"Empty"<<endl;
        return false;
    }
    front = (front + 1) % maxSize;
    return true;
}