SVO中的深度滤波器原理

基础：三角化估计深度

在不同的位置观测同一个三维点P(x, y, z)，已知在不同位置处观察到的三维点的二维投影点p1(x1, y1), p2(x2, y2)，利用三角关系，恢复出三维点的深度信息z。

由于两条直线无法相交，通过最小二乘法求解。

按照对极几何中的定义，设x1, x2为两个特征点的归一化坐标，则它们满足：

s1x1 = s2Rx2 + t                                         公式(1)

左右两侧分别乘以x1^，得：

s1x1^x1 = 0 = s2x1^R x2 +x1^ t

可以先求出s2，再求s1.最后得到特征点的空间位置。

---

 

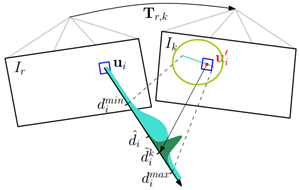
Mapping部分主要是计算特征点的深度。单目VO中，刚刚从图像中提取的热乎的关键点是没有深度的，需要等相机位移之后再通过三角化估计深度。我们知道通过两帧图像的匹配点就可以计算出这一点的深度值，如果有多幅图像，那就能计算出这一点的多个深度值。这就像对同一个状态变量我们进行了多次