数模1 Dijstra与Floyd算法

一、Dijstra算法

1、概述

算法能求一个顶点到另一个顶点最短路径。

1）算法思想

顶点集合分成两组，S，U

第一组为已求出最短路径的顶点集合（用S表示，初始时S中只有一个源点，以后每求得一条最短路径 , 就将加入到集合S中，直到全部顶点都加入到S中，算法就结束了），第二组为其余未确定最短路径的顶点集合（用U表示），按最短路径长度的递增次序依次把第二组的顶点加入S中。

2）算法步骤

a.初始化：S只包含源点，即S＝{v}，v的距离为0。U={其余顶点}，若v与U中顶点u有边，则<u,v>正常有权值，若u不是v的出边邻接点，则<u,v>权值为∞。

b,经过中间点比原来距离短，若cost[j]+graph[j,k]<cost[k] ，则修改cost[k]为：cost[k]=cost[j]+graph[j,k] 。

c.重复上述步骤，直到目标顶点的标号改完。

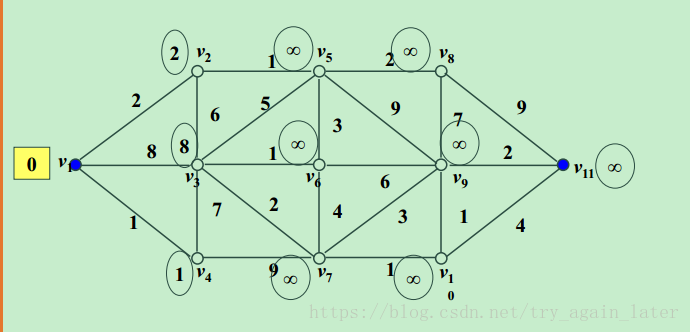
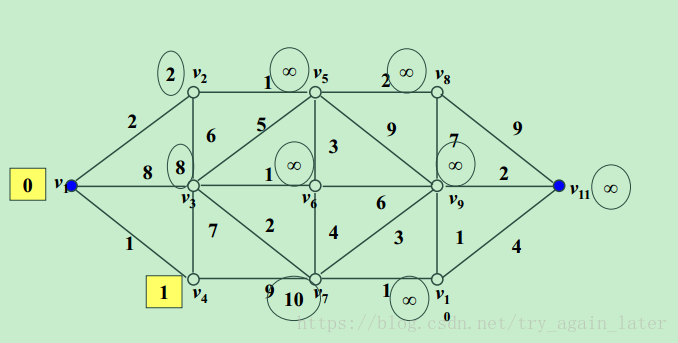
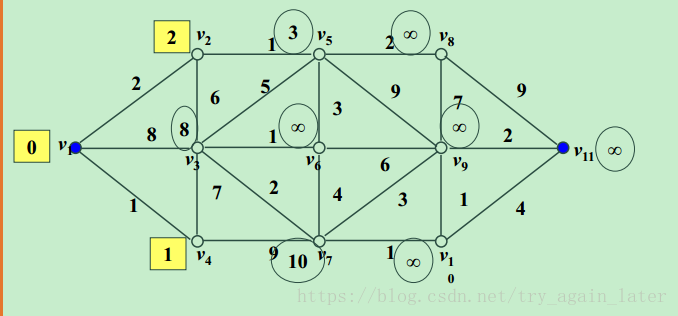
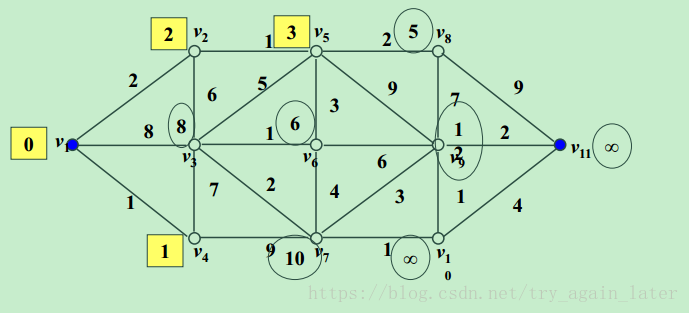
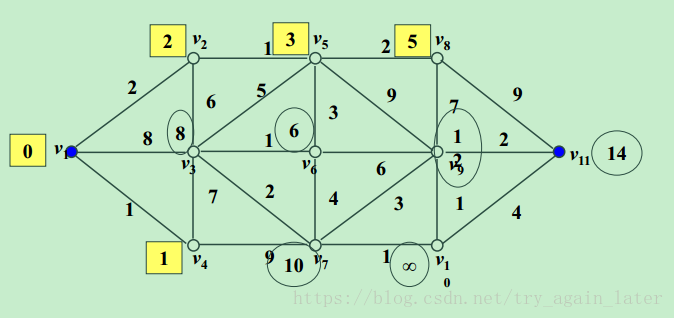
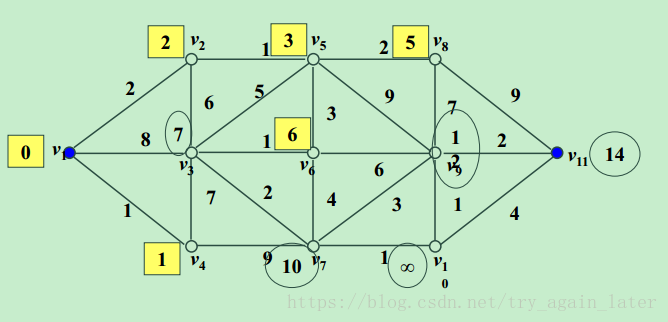
2、代码

matlab调用方式：[dis, path]=dijkstra(weight,1, 11)

dis =   13

path = 1     2     5     6     3     7    10     9    11

更改变量为weight

二、Floyd算法

1、概述

1）算法思想

从任意节点i到任意节点j的最短路径不外乎2种可能，1是直接从i到j，2是从i经过若干个节点k到j。所以，我们假设Dis(i,j)为节点u到节点v的最短路径的距离，对于每一个节点k，我们检查Dis(i,k) + Dis(k,j) < Dis(i,j)是否成立，如果成立，证明从i到k再到j的路径比i直接到j的路径短，我们便设置Dis(i,j) = Dis(i,k) + Dis(k,j)，这样一来，当我们遍历完所有节点k，Dis(i,j)中记录的便是i到j的最短路径的距离。

他每次都会选择一个中介点，然后，遍历整个矩阵，查找需要更新的值，

2）算法步骤

a.从任意一条单边路径开始。所有两点之间的距离是边的权，如果两点之间没有边相连，则权为无穷大。 　　

b.对于每一对顶点 u 和 v，看看是否存在一个顶点 w 使得从 u 到 w 再到 v 比己知的路径更短。如果是更新它。

2、代码

matlab调用方式：[D, path]=floyd(a)

D =                                               

     0    35    45    35    25    10
    35     0    15    20    30    25
    45    15     0    10    20    35
    35    20    10     0    10    25
    25    30    20    10     0    35
    10    25    35    25    35     0

path =

     1     6     5     5     5     6
     6     2     3     4     4     6
     5     2     3     4     5     4
     5     2     3     4     5     6
     1     4     3     4     5     1
     1     2     4     4     1     6

三、二者关系

dijkstra算法是计算单源最短路径。也就是只有一个源点，到各个点的最短路径。
floyd算法是多源最短路径，计算的是各个点之间的最短路径。