一、二叉树基本概念
度:节点拥有的子树个数。
树的度:内部结点度的最大值。
叶子:度为0的节点(没有分出的子节点)
节点层次:根在第一层,树的深度(高度)是最大的层次。
二叉树的五种
空二叉树、只有根节点、根节点只有左子树、只有右子树、左右子树。
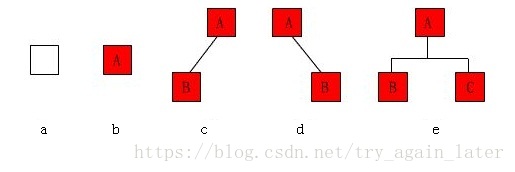
特殊二叉树
满二叉树:所有节点都有左子树和右子树。
完全二叉树:最下一层节点集中在最左边。和满二叉树的编号相同,表明叶子上一层是满二叉树,叶子层从左侧开始。
性质:
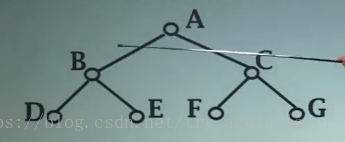
1、第i层上最多有2^(i-1)个节点 (1、2、4)
2、深度为k的满二叉树有2^k-1个节点 (1、3、7)
3、终端叶子为n0,度为2的节点为n2个,则n0=n2+1
推导:分支总数 n0+n1+n2-1=n1+n2*2
4、具有n个节点个完全二叉树的深度为【log2 n】+1(【】表示取整)
具有n个节点个满二叉树的深度为log2(n+1)
完全二叉树的性质 :
设一棵有n个结点的完全二叉树的所有结点按层次从左至右编号为从0到n-1,设某个结点的序号为i,0<=i< n,那么有如下性质:
(1)i=1,说明该结点是根结点。
(2)i>1,说明该结点的父结点为【i/2】(【】表示取整)。
(3)左孩子是节点2*i
(4)右孩子是节点2*i+1。
存储结构
顺序存储结构只适用于完全二叉树(否则左侧有大量空单元)
二叉链表和三叉链表

二、树基本概念
1、有向有序树:子树的相对次序最重要。

2、链式存储结构:
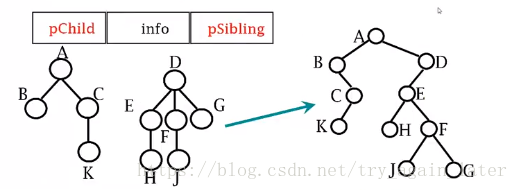
动态“左子/右兄”二叉链表示法:左孩子是节点最左侧子节点,节点原来的右侧兄弟节点
将一棵复杂的树变成一棵二叉树
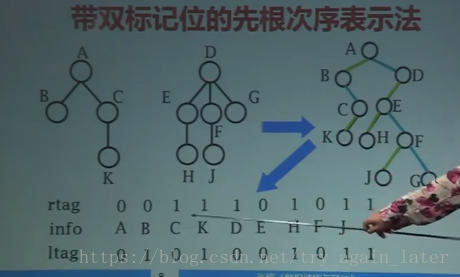
3、顺序存储结构
4、父指针表示法
路径压缩(并不关心H E D之间关系,只要求H的根节点D,直接指向根节点)

路径压缩使Find开销接近于常数。
三、转化关系
树化为二叉树:
1、加线:兄弟之间加一条线,这些线之后不去
2、去线:只留下长子
3、调整:顺时针旋转下,第一个孩子转换为右孩子
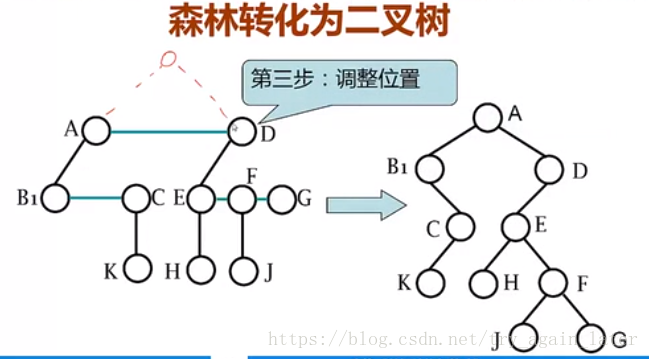
森林转化为二叉树:
1、每棵树转化为二叉树
2、第一棵二叉树不动,从第二棵开始,后一棵的根作为前一棵根节点的右孩子。
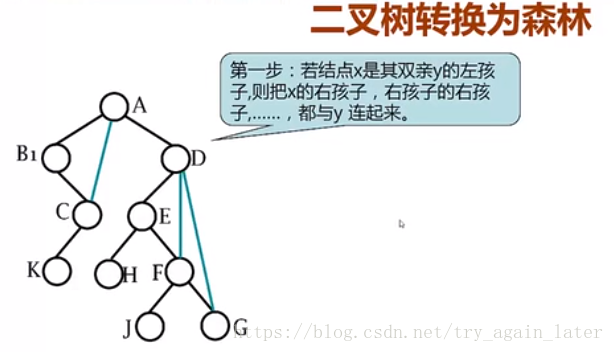
二叉树转为森林
1、加线:若左孩子存在,右孩子节点,右孩子的右孩子。。。。。都和双亲连上
2、去线:删除原来右孩子的连线
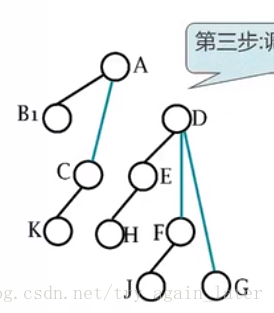
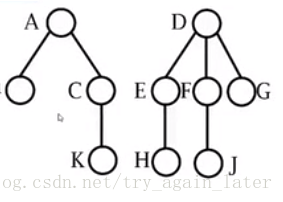





 本文介绍了二叉树的基本概念,包括节点度、树的度、叶子节点和层次。详细阐述了二叉树的五种类型、满二叉树和完全二叉树的特性,并提供了完全二叉树的节点计数公式。此外,讨论了树的存储结构,如顺序存储和链式存储。接着,概述了树的基本概念,包括有向有序树和不同存储方式。最后,探讨了树与二叉树之间的转化关系及其操作方法。
本文介绍了二叉树的基本概念,包括节点度、树的度、叶子节点和层次。详细阐述了二叉树的五种类型、满二叉树和完全二叉树的特性,并提供了完全二叉树的节点计数公式。此外,讨论了树的存储结构,如顺序存储和链式存储。接着,概述了树的基本概念,包括有向有序树和不同存储方式。最后,探讨了树与二叉树之间的转化关系及其操作方法。
















 1175
1175

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








