串、KMP匹配算法

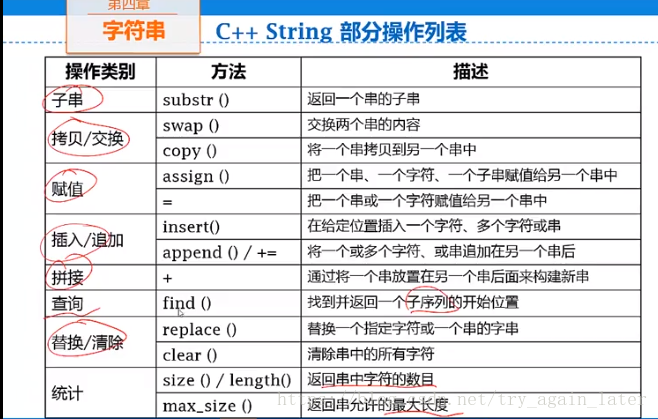
1、基本操作

//串的长度
int strlen(char* s);
//串复制
char* strcpy(char* s1, char* s2);
//串拼接
char* stract(char* s1, char* s2);
//串比较
int strcmp(char* s1, char* s2);

//求字符串长度
int strlen(char d[])
{
	int i = 0;
	while (d[i] != '\0')
		i++;
	return i;
}
//字符串复制
char* strcpy(char* d, char* s)
{
	int i = 0;
	while (s[i] != '\0')
	{
		//要穷尽所有的下标，不能直接d=s
		d[i] = s[i];
		i++;
	}
	d[i] = '\0';
	return d;
}
//字符串的比较
int strcmp(const char* s1, const char* s2)
{
	int i = 0;
	while (s1[i] != '\0'&&s2[i] != '\0')
	{
		if (s1[i] > s2[i])
			return 1;
		else if (s1[i] < s2[i])
			return -1;
		i++;
	}
	if (s1[i] == '\0'&&s2[i] != '\0')
		return -1;
	else if (s2[i] == '\0'&&s1[i] != '\0')
		return 1;
	return 0;
}
//简便的字符串比较
int strcmp(char* s1, char* s2)
{
	for (int i = 0; s1[i] == s2[i]; ++i)
	{
		if (s1[i] == '\0'&& s2[i] == '\0')
			return 0;
	}
	return (s1[i] - s2[i]) / abs(s1[i] - s2[i])
}

构造函数

string::string(char* s)
{
	//确定所需存储空间
	size = strlen(s);
	//动态存储区开辟空间，存储初值s
	str = new char[size + 1];
	//运行异常，退出
	assert(str != NULL);
	//将s复制到指针str所指存储空间
	strcpy(str, s;)
}

析构函数

string::string()
{
	//释放动态内存空间
	delete[]str;
}

赋值运算

string string::operator=(string& s)
{
	//串长不同，释放本串空间开辟新空间
	if (size != s.size)
	{
		delete[]str;
		str = new char[s.size + 1];
		assert(str != NULL);
		size = s.size;
	}
	strcpy(str, s.str);
	return *this;
}

2、朴素的模式匹配（穷举法）

#include <iostream>
#include <string>
using namespace std;
// 暴力匹配
int Naive(string S, string P){
	int s_len = S.size();
	int p_len = P.size();
	int i = 0, j = 0;

	while (i < s_len&&j < p_len){
		if (S[i] == P[j]){// 相等，都前进一步
			i++;
			j++;
		}
		else{// 不相等，i退回到这次匹配首位的下一位
			i = i - j + 1;
			j = 0;
		}
	}

	if (j == p_len)
		return i - j;

}
int main(){
	cout << Naive("bbcabcdababcdabcdabde", "abcdabd") << endl;
	return 0;
}

朴素匹配效率慢的原因是有冗余，明显的不匹配无需再内部遍历比较

时间复杂度为 O(n^2)

---

3、KMP（无回溯匹配）

KMP算法是用来求一个较长字符串是否包含另一个较短字符串的算法。

1、S：“abcdefgab”   T:"abcdex"  

前五位分别相等，所以（abcde）2、3、4、5的比对判断都是多余的。只留下1（a）与6（e）。

1）T中第一位与后4位都不相等；2）T中后4位与S对应4位分别相等，所以T的第一位不可能和S中2、3、4、5相等。

 

2、S：“abcababca”   T:"abcabx"（子串T中有与首字符相等的字符）

1）abc分别相等，可以省去2、3步骤

2）T中ab 与 后面的ab 相等；3）T后面的ab 在第一次比对中和S对应的ab 相等；所以T首字符ab 也和S后面ab相等，省去4、5

总结：利用已经部分匹配这个有效信息，保持i指针不回溯，通过修改j指针，让模式串（子串）尽量地移动到有效的位置

      "部分匹配"的实质是，有时候，字符串头部和尾部会有重复。T串的下标J值取决于当前字符之前的串的前后缀的相似度；

      T="abcdex"没有重复字符，j由6变成1

      T="abcabx"有两个重复字符，j由6变成3（前面ab和主串是相同的） 

      S与T总共5位已匹配的字符，j=6时T中有2位相等，直接向后移动3位。

（子串T向后移动位数 = 已匹配的字符数 - 对应的部分匹配值）5-2=3；j=1+2=3；

next数组

求next数组重点参考：

https://www.jianshu.com/p/bc39539c1db4

https://segmentfault.com/a/1190000008575379

next数组中储存的是这个字符串前缀和后缀中相同字符串的最长长度。next[i]等于P[0]...P[i - 1]最长的相同真前后缀的长度

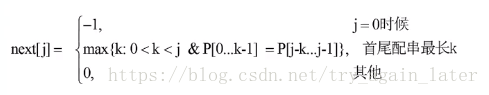
前缀：除了最后一个字符；后缀：除了第一个字符。

代码：

void getnext(char* p, int* next)
{
	int len = strlen(p);
	next[0] = -1;
	int k = -1;
	int j = 0;
	while (j < len - 1)
	{
		//p[k]前缀,p[j]后缀
		if (k == -1 || p[j] == p[k])
		{
			next[++j] = ++k;//p[i]=p[j]时，next下位置就是k加一
		}
		else
		{
			k = next[k];//不相等，回溯，找小范围
		}
	}
}

 代码注释：

在这一步我认为首先要搞清楚的点是：
1. 当前的next[i]是已知的。假设i和j的位置如上图，由next[i] = j得，也就是对于位置i来说，

     区段[0, i - 1]的最长相同真前后缀分别是[0, j - 1]和[i - j, i - 1]，即这两区段内容相同。
2. 我们当前要做的是求解next[i+1]

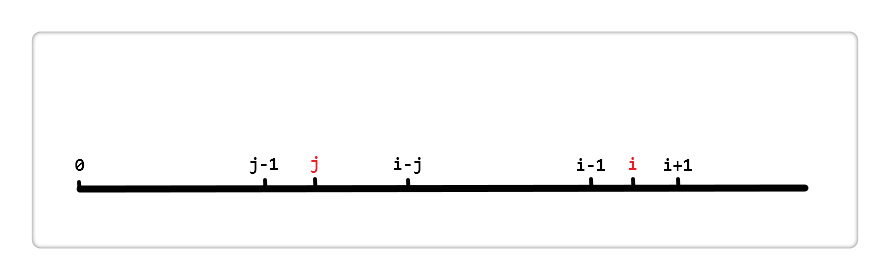
第一种情况：

1. 只要str[i] === str[j]，则两个相同子串的区间长度自然增长了，即[0, j]与[i - j, i]相等，即next[i + 1] = j。

第二种情况：

     2.如果str[i] !== str[j]，我们就需要在[0, j-1]中缩减子串的长度找到一个点k，使得[0, k]这个子串与[i - k, i - 1]子串相等：

既然str[i] !== str[j]了，不能逃避，要找到一个K满足str[K]==str[i],且0~~K和i-K~~i 两段相同。

这样才能继续推导next[i+1]。

下图求K：从左至右我们为绿圈编号1，2，3，4
既然K就是next[j]，则 绿圈1和绿圈2相等，因为第一点说的[0, j - 1]与[i - j, i - 1]相等则从i-j往右扩充K个字符的绿圈3必定有一段绿圈4相等，即我们找到了一个K值，满足了绿圈1与绿圈4相等。

如果递归直到k == -1，则说明找不到相同的前后缀，next[j + 1] = 0

---

 

 

#include <iostream>
#include <string>
using namespace std;
// 获取next数组，这样保证i指针不回溯，修改j指针
// i,j两个指针，寻找最长的相同前后缀0~~j-1和i-j~~i-1
void GetNext(string P, int next[]){
	int p_len = P.size();
	int j = -1; // 前缀
	int i = 0;// 后缀
	next[0] = -1;// 特殊边界，模式串首字符统一为next[0]= -1

	while (i < p_len - 1){
		// 1、首字符之后第一个字符要从-1变成0。2、已知next[i]=j了，当前相同则next[++i] = ++j
		if (j == -1 || P[i] == P[j])
			next[++i] = ++j;// i要前进
		// 当前ij字符不相同，j 回溯，将新的K值赋给了j
		// 之后继续判断P[i]是否等于P[K],等于我们要为P[i]找一个相等的数，满足0~~K和 i-K~~i相同，这样才能继续算next[i+1]
		else
			j = next[j];
	}
}

// KMP算法
int KMP(string S, string P){
	int next[100];
	GetNext(P, next); //变化1、先根据子串P获取next数组

	int s_len = S.size();
	int p_len = P.size();
	int i = 0, j = 0;

	while (i < s_len&&j < p_len){
		if (S[i] == P[j]){// 相等，都前进一步
			i++;
			j++;
		}
		else{
			j = next[j];// 变化2、当前匹配失败，j跳转next数组，和之前相比，i不用回溯了。
		}
	}
	// 匹配成功，i的位置减去匹配串的长度j就是匹配串出现的位置索引
	if (j == p_len)
		return i - j;
	else
		return -1;// 匹配失败

}
int main(){
	cout << KMP("bbcabcdababcdabcdabde", "abcdabd") << endl;
	return 0;
}