P1036 [NOIP 2002 普及组] 选数
题目描述
已知 nnn 个整数 x1,x2,⋯ ,xnx_1,x_2,\cdots,x_nx1,x2,⋯,xn,以及 111 个整数 kkk(k<nk<nk<n)。从 nnn 个整数中任选 kkk 个整数相加,可分别得到一系列的和。例如当 n=4n=4n=4,k=3k=3k=3,444 个整数分别为 3,7,12,193,7,12,193,7,12,19 时,可得全部的组合与它们的和为:
3+7+12=223+7+12=223+7+12=22
3+7+19=293+7+19=293+7+19=29
7+12+19=387+12+19=387+12+19=38
3+12+19=343+12+19=343+12+19=34
现在,要求你计算出和为素数共有多少种。
例如上例,只有一种的和为素数:3+7+19=293+7+19=293+7+19=29。
输入格式
第一行两个空格隔开的整数 n,kn,kn,k(1≤n≤201 \le n \le 201≤n≤20,k<nk<nk<n)。
第二行 nnn 个整数,分别为 x1,x2,⋯ ,xnx_1,x_2,\cdots,x_nx1,x2,⋯,xn(1≤xi≤5×1061 \le x_i \le 5\times 10^61≤xi≤5×106)。
输出格式
输出一个整数,表示种类数。
输入输出样例
输入
4 3
3 7 12 19
输出
1
说明/提示
【题目来源】
NOIP 2002 普及组第二题
解析
利用回溯法将数组组合,然后判断是否是质数即可
import java.util.Scanner;
public class Main {
static int[] nums;
static int n, k;
static int count = 0;
/**
* 判断是否为素数
*/
public static boolean isPrime(int num){
if (num < 2) {
return false;
}
for (int i = 2; i < Math.sqrt(num); i++){
if (num % i == 0) {
return false;
}
}
return true;
}
public static void dfs(int start, int selected, int sum) {
if (selected == k){
if (isPrime(sum)) {
count++;
}
return;
}
for (int i = start; i < n; i++){
dfs(i + 1, selected + 1, sum + nums[i]);
}
}
public static void main(String[] args) {
Scanner scanner = new Scanner(System.in);
n = scanner.nextInt();
k = scanner.nextInt();
nums = new int[n];
for (int i = 0; i < n; i++){
nums[i] = scanner.nextInt();
}
dfs(0, 0, 0);
System.out.println(count);
scanner.close();
}
}
一、其中判断是否是质数的方法为什么只循环到了num\sqrt{num}num?
答:假设一个数N不是素数,那么它一定可以表示为N = a * b(a,b不能为1和N)
如果a和b都大于num\sqrt{num}num,那么a * b > num
所以N的因子中,其中至少有一个小于等于num\sqrt{num}num
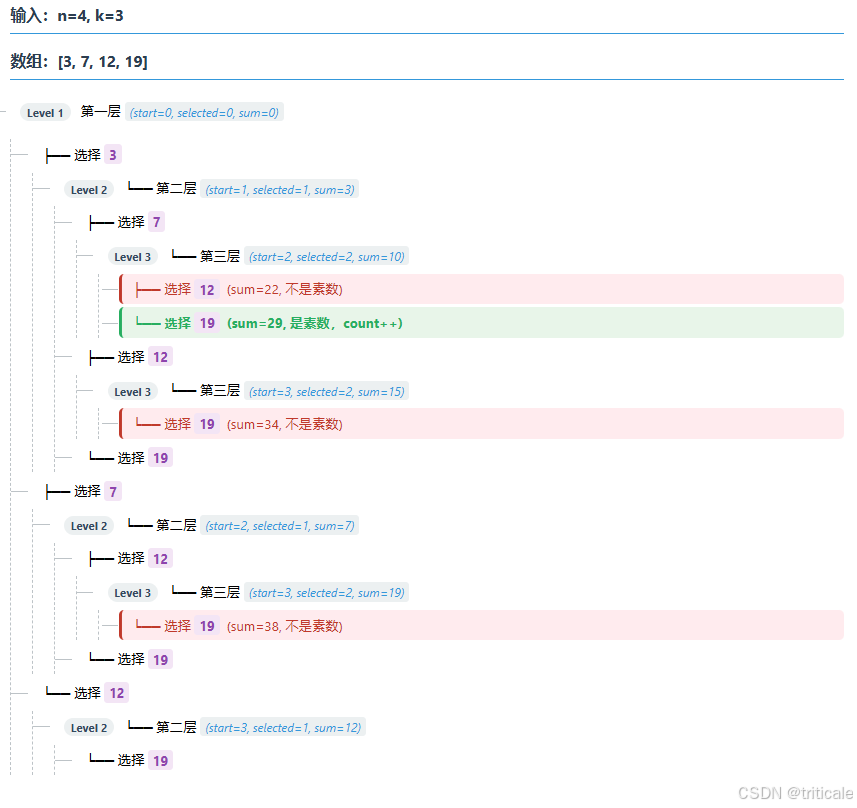
二、递归的过程看不懂怎么办?
答:通过一个具体的例子画图表示





















 880
880

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








