用 NumPy 处理数据快 N 倍：Python 数值计算的 “加速器“ 实战指南

class 卑微码农:
    def __init__(self):
        self.技能 = ['能读懂十年前祖传代码', '擅长用Ctrl+C/V搭建世界', '信奉"能跑就别动"的玄学']
        self.发量 = 100  # 初始发量
        self.咖啡因耐受度 = '极限'
        
    def 修Bug(self, bug):
        try:
            # 试图用玄学解决问题
            if bug.严重程度 == '离谱':
                print("这一定是环境问题！")
            else:
                print("让我看看是谁又没写注释...哦，是我自己。")
        except Exception as e:
            # 如果try块都救不了，那就...
            print("重启一下试试？")
            self.发量 -= 1  # 每解决一个bug，头发-1
 
 
# 实例化一个我
我 = 卑微码农()

引言：处理大数据的“黑科技”

如果你用 Python 处理过大量数据，可能会遇到这样的困惑：“为什么用列表循环计算时，数据量一大就卡得要死？”“别人处理 100 万条数据只要几秒，我的代码却要跑几分钟？”

答案可能就在 NumPy 上。这个被称为 “Python 数值计算基石” 的库，能让你的数据处理速度提升 10 倍甚至 100 倍 —— 不是因为代码写得更巧，而是 NumPy 底层用 C 语言实现，绕开了 Python 的解释器瓶颈，还能像 “向量运算” 一样批量处理数据，不用写循环。

今天这篇文章，我会从 “为什么 NumPy 比列表快” 讲起，手把手教你用 NumPy 处理实际问题：从基础的数组创建，到复杂的图像像素操作，全程用生活化的例子解释概念，代码复制就能跑。哪怕是刚接触数值计算的新手，也能搞懂 NumPy 的核心用法，让数据处理效率飙升。

一、为什么 NumPy 是数据处理的 “加速器”？先看一组对比

第一次用 NumPy 时，我被它的速度震惊了 —— 同样是计算 100 万个数字的平方和，用 Python 列表循环要 5 秒，用 NumPy 只要 0.005 秒，快了 1000 倍！

我们用代码直观对比一下：

import time
import numpy as np

# 生成100万个随机数
python_list = [i for i in range(1000000)]
numpy_array = np.arange(1000000)

# 用Python列表计算平方和（循环）
start = time.time()
sum_squares_python = sum(x**2 for x in python_list)
end = time.time()
print(f"Python列表耗时：{end - start:.4f}秒")  # 约0.1-0.3秒（因电脑而异）

# 用NumPy计算平方和（向量运算）
start = time.time()
sum_squares_numpy = np.sum(numpy_array** 2)
end = time.time()
print(f"NumPy数组耗时：{end - start:.4f}秒")  # 约0.001-0.003秒

运行结果显示，NumPy 的速度是纯 Python 的 100 倍以上。这还只是简单计算，数据量越大、运算越复杂，差距越明显。

为什么 NumPy 这么快？核心原因有两个：

存储效率高：Python 列表存储的是一个个 Python 对象（每个数字占 28 字节），而 NumPy 数组所有元素共用一个数据类型，存储在连续的内存块中（比如 32 位整数每个只占 4 字节），内存占用仅为列表的 1/7；
向量化运算：NumPy 不用写循环，直接对整个数组做运算（比如array **2会给每个元素平方），底层用 C 语言实现，避开了 Python 解释器的速度限制。

简单说：NumPy 把 “用 Python 循环逐个处理元素” 变成了 “用 C 语言批量处理整块数据”，这就是它快的本质。

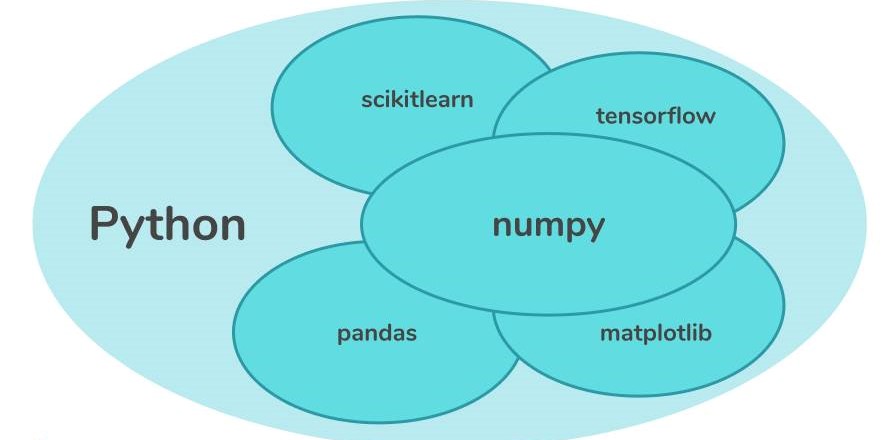
除了快，NumPy 还是数据分析的 “基础设施”：Pandas 的 DataFrame 基于 NumPy 构建，Matplotlib、Seaborn 绘图时依赖 NumPy 处理数据，机器学习库 Scikit-learn、深度学习框架 TensorFlow/PyTorch 的底层数据结构也是 NumPy 数组。学好 NumPy，相当于给数据分析、机器学习打下了基石。

二、环境搭建：2 步搞定 NumPy 开发环境（附版本选择）

NumPy 的安装和使用非常简单，支持 Windows、macOS、Linux，这里以 “Windows 10+Python 3.9” 为例，其他系统操作基本一致。

步骤 1：安装 NumPy

打开 cmd（Windows）或终端（macOS/Linux），直接用 pip 安装：

pip install numpy==1.24.3  # 1.24.3是稳定版，兼容性好，支持Python 3.8+

如果你的电脑装了 Anaconda，自带 NumPy，不用重复安装，直接用即可。

步骤 2：验证安装是否成功

打开 Python 交互式环境（输入python），运行以下代码：

import numpy as np
print(np.__version__)  # 输出1.24.3说明安装成功
# 简单测试：创建一个数组并计算
arr = np.array([1, 2, 3])
print(arr * 2)  # 输出[2 4 6]，表示正常工作

常见坑点：

安装时报 “超时错误”：用国内镜像加速，比如pip install numpy -i https://pypi.tuna.tsinghua.edu.cn/simple；
导入时提示 “ModuleNotFoundError”：检查是否拼写错误（是numpy不是numpi），或重新安装；
版本不兼容：如果用的 Python 是 3.7 及以下，建议安装 NumPy 1.21.x 版本（pip install numpy==1.21.6）。

三、核心概念：用 “超级列表” 理解 NumPy 数组

很多人学 NumPy 时被 “维度”“轴”“数据类型” 这些术语搞晕，其实可以把 NumPy 的核心对象 ——ndarray（N 维数组） 理解成 “功能增强的超级列表”。

我们用生活化的例子解释几个关键概念：

1. 数组 vs 列表：不只是 “长得像”

普通列表：像一个 “杂货袋”，可以装不同类型的东西（数字、字符串、列表等），比如[1, "a", [2,3]]；
NumPy 数组：像一个 “整齐的抽屉”，只能装同一种类型的数据（比如全是整数或全是浮点数），且存储在连续的内存中。

这种 “单一类型” 和 “连续存储” 的特性，正是 NumPy 速度快的关键。

2. 维度（ndim）：数组的 “维度” 就是 “层数”

0 维数组：单个数字，像抽屉里的一个小球，比如np.array(5)；
1 维数组：一行数字，像排成一列的小球，比如np.array([1,2,3])（类似列表）；
2 维数组：行列结构，像表格或矩阵，比如np.array([[1,2],[3,4]])（类似 Excel 表格）；
3 维数组：多个 2 维数组堆叠，像一叠表格，比如np.array([[[1,2],[3,4]], [[5,6],[7,8]]])（可以理解为 “页 - 行 - 列”）。

维度可以用ndim属性查看，比如 2 维数组的ndim是 2。

3. 形状（shape）：用元组表示各维度的长度

1 维数组[1,2,3]的形状是(3,)（表示有 3 个元素）；
2 维数组[[1,2],[3,4]]的形状是(2,2)（2 行 2 列）；
3 维数组[[[1,2],[3,4]], [[5,6],[7,8]]]的形状是(2,2,2)（2 页、2 行、2 列）。

形状用shape属性查看，修改形状可以改变数组的组织方式（比如把 6 个元素的 1 维数组改成 2×3 的 2 维数组）。

4. 数据类型（dtype）：数组中元素的类型

NumPy 支持更多数据类型，比 Python 内置类型更精细，比如：

int32：32 位整数（范围 - 2^31 到 2^31-1）；
float64：64 位浮点数（双精度，默认类型）；
bool：布尔值（True/False）；
string_：字符串类型。

数据类型用dtype属性查看，创建数组时可以指定，比如np.array([1,2], dtype=np.float64)。

四、实战：NumPy 核心操作（从创建到运算，附代码 + 效果）

下面从 “创建数组” 到 “高级运算”，用实例讲解 NumPy 的核心用法，所有代码可直接复制运行，建议边练边理解。

场景 1：创建数组（4 种常用方式）

创建数组是 NumPy 的基础，掌握这 4 种方式，能应对 90% 的场景。

1. 从 Python 列表创建（最直接）

用np.array()把列表转换成 NumPy 数组，支持嵌套列表（创建多维数组）：

import numpy as np

# 1维数组
arr1d = np.array([1, 2, 3, 4, 5])
print("1维数组：", arr1d)
print("维度：", arr1d.ndim)  # 输出1
print("形状：", arr1d.shape)  # 输出(5,)
print("数据类型：", arr1d.dtype)  # 输出int32（默认，因系统而异）

# 2维数组（嵌套列表）
arr2d = np.array([[1, 2, 3], [4, 5, 6]])
print("\n2维数组：\n", arr2d)
print("维度：", arr2d.ndim)  # 输出2
print("形状：", arr2d.shape)  # 输出(2,3)（2行3列）

# 指定数据类型
arr_float = np.array([1, 2, 3], dtype=np.float64)
print("\n指定float类型：", arr_float)  # 输出[1. 2. 3.]

注意：如果列表中元素类型不同，NumPy 会自动向上转换（比如 int 和 float 混合，结果是 float）。

2. 用内置函数创建（高效生成规则数组）

当需要生成有规律的数组（比如 0-9 的数字、全 0 数组），用 NumPy 的内置函数比手动写列表快得多：

# 生成0-9的整数（类似range，但返回数组）
arr_range = np.arange(10)
print("arange(10)：", arr_range)  # [0 1 2 3 4 5 6 7 8 9]

# 生成从2开始，步长为3，不超过20的数
arr_step = np.arange(2, 20, 3)
print("arange(2,20,3)：", arr_step)  # [ 2  5  8 11 14 17]

# 生成5个从0到1的均匀分布的数（包括0和1）
arr_lin = np.linspace(0, 1, 5)
print("linspace(0,1,5)：", arr_lin)  # [0.   0.25 0.5  0.75 1.  ]

# 生成2×3的全0数组
arr_zero = np.zeros((2, 3))
print("\nzeros((2,3))：\n", arr_zero)

# 生成3×2的全1数组，指定int类型
arr_one = np.ones((3, 2), dtype=np.int32)
print("ones((3,2))：\n", arr_one)

# 生成2×2的单位矩阵（对角线为1，其余为0）
arr_eye = np.eye(2)
print("eye(2)：\n", arr_eye)

区别：arange按步长生成，linspace按个数生成，按需选择（比如画函数图像常用linspace生成等间隔的 x 值）。

3. 生成随机数组（模拟数据常用）

数据分析中常需要模拟数据，NumPy 的random模块提供了各种随机数组生成方法：

# 设置随机种子（让结果可重复）
np.random.seed(42)

# 生成3个[0,1)之间的随机浮点数
rand_float = np.random.random(3)
print("随机浮点数：", rand_float)  # [0.37454012 0.95071431 0.73199394]

# 生成2×2的随机整数（范围[1,10)）
rand_int = np.random.randint(1, 10, size=(2, 2))
print("2×2随机整数：\n", rand_int)
# 输出（因种子固定，结果固定）：
# [[7 4]
#  [8 5]]

# 生成3个符合正态分布（均值0，标准差1）的数
rand_norm = np.random.normal(0, 1, 3)
print("正态分布随机数：", rand_norm)  # [-0.23415337 -0.23413696  1.57921282]

# 从列表中随机选择3个元素（可重复）
rand_choice = np.random.choice([10, 20, 30, 40], 3)
print("随机选择：", rand_choice)  # [40 20 20]

应用：随机数组常用于模拟实验数据（如模拟学生成绩、产品销量），np.random.seed(42)确保代码每次运行结果一致，方便调试。

4. 从文件读取数组（处理实际数据）

实际工作中，数据常存在 CSV、TXT 文件中，用np.loadtxt或np.genfromtxt读取：

假设我们有一个data.csv文件，内容如下（逗号分隔）：

1,2,3
4,5,6
7,8,9

读取代码：

# 读取CSV文件（默认空格或逗号分隔）
data = np.loadtxt("data.csv", delimiter=",")
print("从文件读取的数组：\n", data)
# 输出：
# [[1. 2. 3.]
#  [4. 5. 6.]
#  [7. 8. 9.]]

# 读取时指定数据类型为int
data_int = np.loadtxt("data.csv", delimiter=",", dtype=np.int32)
print("int类型数据：\n", data_int)

注意：如果文件有缺失值，用np.genfromtxt更合适，可指定缺失值填充方式（如filling_values=0）。

场景 2：数组操作（索引、切片、重塑）

拿到数组后，需要提取或修改其中的数据，NumPy 的索引和切片比列表更灵活，还能重塑数组形状。

1. 索引：获取单个元素（和列表类似，但支持多维）

# 1维数组索引（和列表一样）
arr1d = np.arange(10)
print("arr1d[3] =", arr1d[3])  # 输出3（第4个元素，从0开始）
print("arr1d[-1] =", arr1d[-1])  # 输出9（最后一个元素）

# 2维数组索引（行索引, 列索引）
arr2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print("\narr2d[1,2] =", arr2d[1, 2])  # 输出6（第2行第3列）
# 也可以写成arr2d[1][2]，但推荐用逗号分隔，更高效

# 3维数组索引（页索引, 行索引, 列索引）
arr3d = np.array([
    [[1, 2], [3, 4]],
    [[5, 6], [7, 8]]
])
print("arr3d[0,1,0] =", arr3d[0, 1, 0])  # 输出3（第1页第2行第1列）

2. 切片：获取子数组（批量提取元素）

切片格式：start:end:step（start 默认 0，end 默认数组长度，step 默认 1）

# 1维数组切片
arr1d = np.arange(10)
print("arr1d[2:5] =", arr1d[2:5])  # [2 3 4]（从索引2到4，不包括5）
print("arr1d[:5] =", arr1d[:5])    # [0 1 2 3 4]（从开头到4）
print("arr1d[5:] =", arr1d[5:])    # [5 6 7 8 9]（从5到结尾）
print("arr1d[::2] =", arr1d[::2])  # [0 2 4 6 8]（步长2，取偶数索引）

# 2维数组切片（行切片, 列切片）
arr2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
print("\n取前2行，所有列：\n", arr2d[:2, :])
# 输出：
# [[1 2 3]
#  [4 5 6]]

print("取所有行，第2列：\n", arr2d[:, 1:2])  # 保持2维结构
# 输出：
# [[2]
#  [5]
#  [8]]

print("取第2-3行，第1-2列：\n", arr2d[1:, :2])
# 输出：
# [[4 5]
#  [7 8]]

技巧：切片得到的是原数组的 “视图”（不是副本），修改切片会影响原数组。如果要复制，用arr[slice].copy()。

3. 重塑（reshape）：改变数组形状（不改变数据）

重塑数组时，新形状的元素总数必须和原数组相同（比如 6 个元素可重塑为 2×3 或 3×2）。

# 把1维数组重塑为2×3的2维数组
arr = np.arange(6)
arr_2d = arr.reshape(2, 3)
print("重塑为2×3：\n", arr_2d)
# 输出：
# [[0 1 2]
#  [3 4 5]]

# 重塑为3维数组（1页2行3列）
arr_3d = arr.reshape(1, 2, 3)
print("重塑为1×2×3：\n", arr_3d)

# 用-1自动计算维度（比如6个元素，指定2行，列数自动为3）
arr_auto = arr.reshape(2, -1)
print("自动计算列数：\n", arr_auto)  # 结果同上2×3

# 展平数组（变成1维）
arr_flat = arr_2d.flatten()
print("展平数组：", arr_flat)  # [0 1 2 3 4 5]

应用：处理图像数据时常用重塑，比如把 (28,28) 的图像数组（2 维）展平成 784 的 1 维数组，用于机器学习输入。

场景 3：数组运算（不用循环的批量操作）

NumPy 的 “向量化运算” 是核心优势，不用写 for 循环，直接对整个数组做运算，代码简洁且速度快。

1. 元素级运算（每个元素单独参与）

arr = np.array([1, 2, 3, 4])

# 算术运算（加、减、乘、除、平方）
print("arr + 2 =", arr + 2)  # [3 4 5 6]
print("arr * 3 =", arr * 3)  # [3 6 9 12]
print("arr / 2 =", arr / 2)  # [0.5 1.  1.5 2. ]
print("arr **2 =", arr** 2)  # [ 1  4  9 16]

# 两个数组运算（对应元素操作，要求形状相同）
arr2 = np.array([5, 6, 7, 8])
print("arr + arr2 =", arr + arr2)  # [ 6  8 10 12]
print("arr * arr2 =", arr * arr2)  # [ 5 12 21 32]

对比：如果用 Python 列表，[1,2,3,4] + 2会报错，必须写循环[x+2 for x in list]，而 NumPy 直接支持，既简洁又高效。

2. 统计运算（求总和、均值、标准差等）

NumPy 提供了丰富的统计函数，可对整个数组或指定轴（维度）计算：

arr2d = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])

# 计算整个数组的统计量
print("总和：", arr2d.sum())       # 45（1+2+...+9）
print("均值：", arr2d.mean())      # 5.0
print("标准差：", arr2d.std())     # 2.581988897471611
print("最大值：", arr2d.max())     # 9
print("最小值：", arr2d.min())     # 1
print("最大值索引：", arr2d.argmax())  # 8（扁平化后的索引）

# 按轴计算（axis=0按列，axis=1按行）
print("\n按列求和：", arr2d.sum(axis=0))  # [12 15 18]（1+4+7=12，以此类推）
print("按行求均值：", arr2d.mean(axis=1))  # [2. 5. 8.]

应用：计算学生成绩表中各科目平均分（按列求均值）、每个学生总分（按行求和），用这些函数一行代码搞定。

3. 矩阵运算（点积、矩阵乘法）

对于 2 维数组，NumPy 支持矩阵运算（线性代数必备）：

# 定义两个矩阵
A = np.array([[1, 2], [3, 4]])
B = np.array([[5, 6], [7, 8]])

# 元素级乘法（和A*B一样）
print("元素乘法：\n", A * B)
# 输出：
# [[ 5 12]
#  [21 32]]

# 矩阵乘法（点积，用@或np.dot）
print("矩阵乘法（A@B）：\n", A @ B)
# 输出：
# [[1*5+2*7 1*6+2*8]
#  [3*5+4*7 3*6+4*8]]
# [[19 22]
#  [43 50]]

# 矩阵转置（行变列，列变行）
print("A的转置：\n", A.T)
# 输出：
# [[1 3]
#  [2 4]]

注意：矩阵乘法要求第一个矩阵的列数等于第二个矩阵的行数（如 2×2 矩阵可乘 2×3 矩阵，结果是 2×3）。

场景 4：广播机制（不同形状数组的运算）

当两个数组形状不同时，NumPy 会触发 “广播机制”，自动扩展数组使其形状匹配，再进行运算。这是 NumPy 最强大的特性之一，能简化很多代码。

1. 广播的简单例子（标量和数组）

arr = np.array([1, 2, 3])
print(arr + 5)  # [6 7 8]

这里标量 5 被 “广播” 成了[5,5,5]，再和 arr 相加，不用手动扩展。

2. 一维数组和二维数组的广播

# 2×3的二维数组
arr2d = np.array([[1, 2, 3], [4, 5, 6]])
# 1×3的一维数组
arr1d = np.array([10, 20, 30])

# 广播后，arr1d被扩展成2×3（和arr2d形状相同）
print(arr2d + arr1d)
# 输出：
# [[11 22 33]
#  [14 25 36]]

3. 广播的规则（必须满足才能广播）

广播不是万能的，需要满足 “形状兼容”：从最后一个维度开始比较，两个维度要么相等，要么其中一个是 1。

比如：

(3,3) 和 (3,)：兼容（最后一个维度都是 3）；
(2,3) 和 (3,2)：不兼容（最后一个维度 3≠2）；
(4,1,3) 和 (2,3)：兼容（第一个数组的第 2 维是 1，可扩展成 2）。

不兼容时会报错 “ValueError: operands could not be broadcast together”，此时需要用reshape调整形状。

五、实战案例：用 NumPy 解决实际问题

学了基础操作，我们用两个实际案例看看 NumPy 的应用，感受它处理数据的高效。

案例 1：分析学生成绩（统计与筛选）

假设有 50 名学生的 3 门科目成绩（语文、数学、英语），用 NumPy 分析成绩分布、计算各科目平均分、筛选优秀学生（总分≥270）。

import numpy as np

# 生成模拟成绩（50行3列，范围[60,100]）
np.random.seed(42)
scores = np.random.randint(60, 101, size=(50, 3))
# 列名：语文、数学、英语
subjects = ["语文", "数学", "英语"]

# 1. 计算各科目平均分、最高分、最低分
avg_scores = scores.mean(axis=0)
max_scores = scores.max(axis=0)
min_scores = scores.min(axis=0)

print("各科目统计：")
for i in range(3):
    print(f"{subjects[i]}：平均分{avg_scores[i]:.1f}，最高分{max_scores[i]}，最低分{min_scores[i]}")

# 2. 计算每个学生的总分
total_scores = scores.sum(axis=1)
print("\n前5名学生总分：", total_scores[:5])

# 3. 筛选优秀学生（总分≥270）
excellent_mask = total_scores >= 270  # 布尔数组（True/False）
excellent_students = scores[excellent_mask]
print(f"\n优秀学生人数：{excellent_students.shape[0]}")
print("优秀学生成绩：\n", excellent_students)

# 4. 计算优秀学生的各科平均分
if excellent_students.size > 0:
    excellent_avg = excellent_students.mean(axis=0)
    print("\n优秀学生各科平均分：")
    for i in range(3):
        print(f"{subjects[i]}：{excellent_avg[i]:.1f}")

运行结果解读：

用randint快速生成 50×3 的成绩矩阵，比手动输入高效；
按轴计算统计量，一行代码得到各科平均分；
用布尔索引（scores[excellent_mask]）筛选优秀学生，不用写循环；
整个过程代码简洁，处理 100 万条数据也能快速完成。

案例 2：处理图像像素（修改图片颜色）

图像在计算机中存储为像素数组（3 维数组：高度 × 宽度 × 通道，RGB 三通道各 0-255），用 NumPy 可快速修改像素值，实现滤镜效果。

步骤 1：准备图片并读取

需要安装PIL库（处理图像）：pip install pillow

import numpy as np
from PIL import Image

# 读取图片（替换成你的图片路径）
img = Image.open("test.jpg")
# 转换为NumPy数组（形状：(高度, 宽度, 3)）
img_array = np.array(img)
print("图像数组形状：", img_array.shape)  # 比如(480, 640, 3)

步骤 2：实现灰度图效果（保留亮度，去除色彩）

灰度图计算公式：gray = 0.299*R + 0.587*G + 0.114*B

# 提取RGB三通道
R = img_array[:, :, 0]
G = img_array[:, :, 1]
B = img_array[:, :, 2]

# 计算灰度值（向量化运算，不用循环）
gray_array = 0.299 * R + 0.587 * G + 0.114 * B
# 转换为整数（像素值是0-255的整数）
gray_array = gray_array.astype(np.uint8)

# 转换回图像并保存
gray_img = Image.fromarray(gray_array)
gray_img.save("gray_test.jpg")

步骤 3：实现反色效果（颜色反转）

反色公式：inverse = 255 - 原像素值

# 反色处理（每个通道都用255减去原像素）
inverse_array = 255 - img_array
# 确保像素值在0-255范围内（防止溢出）
inverse_array = np.clip(inverse_array, 0, 255).astype(np.uint8)

# 保存反色图片
inverse_img = Image.fromarray(inverse_array)
inverse_img.save("inverse_test.jpg")

效果：运行后会生成灰度图和反色图，整个过程用向量化运算处理百万像素，比用 Python 循环快几十倍。

案例 3：数据清洗（处理缺失值与异常值）

场景：实际数据常存在缺失值（如传感器故障）和异常值（如录入错误），用 NumPy 快速检测并处理，为后续分析铺路。

步骤：

生成模拟数据（含缺失值NaN和异常值）；
检测缺失值并填充（用均值）；
检测异常值（用 “3σ 原则”：超过均值 ±3 倍标准差视为异常）并修正。

import numpy as np

# 1. 生成模拟数据（100个样本，3个特征，含缺失值和异常值）
np.random.seed(42)
data = np.random.normal(loc=50, scale=10, size=(100, 3))  # 正态分布数据（均值50，标准差10）
# 随机插入10个缺失值
mask = np.random.choice([True, False], size=data.shape, p=[0.1, 0.9])
data[mask] = np.nan
# 插入5个异常值（远大于正常范围）
outlier_mask = np.random.choice(range(100), size=5, replace=False)
data[outlier_mask, 0] = data[outlier_mask, 0] * 3  # 第一列插入异常值


# 2. 处理缺失值
print(f"原始数据缺失值数量：{np.isnan(data).sum()}")  # 统计缺失值总数

# 按列计算均值（忽略NaN），并用均值填充缺失值
col_means = np.nanmean(data, axis=0)  # 每列均值（nanmean自动忽略NaN）
data_filled = np.where(np.isnan(data), col_means, data)  # 缺失值替换为均值
print(f"填充后缺失值数量：{np.isnan(data_filled).sum()}")  # 确认缺失值已处理


# 3. 处理异常值（以第一列为例）
col = data_filled[:, 0]
mean = np.mean(col)
std = np.std(col)
# 定义异常值边界（3σ原则）
lower_bound = mean - 3 * std
upper_bound = mean + 3 * std

# 检测异常值索引
outliers = (col < lower_bound) | (col > upper_bound)
print(f"异常值索引：{np.where(outliers)[0]}")

# 异常值修正为边界值（截断法）
col[outliers] = np.where(col[outliers] < lower_bound, lower_bound, upper_bound)
data_filled[:, 0] = col

# 验证异常值是否处理完毕
print(f"处理后异常值数量：{np.sum((data_filled[:,0] < lower_bound) | (data_filled[:,0] > upper_bound))}")

结果解读：

用np.isnan快速定位缺失值，np.nanmean计算均值时自动忽略NaN，避免统计偏差；
“3σ 原则” 基于正态分布特性（99.7% 的数据在均值 ±3σ 内），适合快速筛选异常值；
处理后的数据无缺失、无极端值，可直接用于建模或分析。

案例 4：销售数据统计分析

场景：某店铺 12 个月的三类商品销量数据，用 NumPy 计算关键指标（月均销量、增长率、Top 销量月份），辅助业务决策。

import numpy as np
import matplotlib.pyplot as plt

# 1. 生成模拟数据（12个月，3类商品销量）
np.random.seed(42)
months = np.arange(1, 13)  # 1-12月
# 商品A：稳步增长，商品B：波动，商品C：季节性
sales_A = 100 + 5 * months + np.random.randint(-10, 10, size=12)
sales_B = 150 + np.random.randint(-30, 30, size=12)
sales_C = 80 + 30 * np.sin(months * np.pi/6) + np.random.randint(-15, 15, size=12)
sales = np.column_stack((sales_A, sales_B, sales_C))  # 合并为12×3数组（行：月份，列：商品）
products = ["商品A", "商品B", "商品C"]


# 2. 计算核心指标
# 月均销量（按商品）
monthly_avg = sales.mean(axis=0)
# 全年总销量（按商品）
total_sales = sales.sum(axis=0)
# 环比增长率（每月较上月的增长比例，第一月无增长率）
growth_rate = (sales[1:] - sales[:-1]) / sales[:-1] * 100  # 11×3数组


# 3. 输出关键结果
print("=== 各商品全年总销量 ===")
for i, p in enumerate(products):
    print(f"{p}：{total_sales[i]:.0f}件")

print("\n=== 各商品月均销量 ===")
for i, p in enumerate(products):
    print(f"{p}：{monthly_avg[i]:.1f}件")

print("\n=== 商品A销量最高的3个月份 ===")
top3_months = months[np.argsort(sales_A)[-3:][::-1]]  # 按销量排序取前3
print(top3_months)


# 4. 可视化销量趋势（结合Matplotlib）
plt.figure(figsize=(12, 6))
for i in range(3):
    plt.plot(months, sales[:, i], marker="o", label=products[i])
plt.title("2023年各商品销量趋势", fontsize=15)
plt.xlabel("月份")
plt.ylabel("销量（件）")
plt.legend()
plt.grid(alpha=0.3)
plt.show()

结果解读：

用axis=0按列计算均值 / 总和（每个商品的指标），axis=1可按行计算（每月总销量）；
环比增长率用数组切片（sales[1:] - sales[:-1]）实现，无需循环，简洁高效；
结合可视化可直观发现：商品 A 稳步增长，商品 C 有季节性波动（夏季销量高）。

案例 5：图像边缘检测（Sobel 算子实现）

场景：边缘是图像的重要特征（如物体轮廓），用 NumPy 实现 Sobel 算子（一种经典边缘检测算法），通过矩阵卷积提取边缘。

import numpy as np
from PIL import Image
import matplotlib.pyplot as plt

# 1. 读取图像并转为灰度图
img = Image.open("test.jpg").convert("L")  # 转为灰度图（单通道）
img_array = np.array(img, dtype=np.float32)  # 转为数组（形状：高度×宽度）
height, width = img_array.shape


# 2. 定义Sobel算子（水平和垂直方向）
sobel_x = np.array([[-1, 0, 1], [-2, 0, 2], [-1, 0, 1]])  # 检测水平边缘（左右变化）
sobel_y = np.array([[-1, -2, -1], [0, 0, 0], [1, 2, 1]])  # 检测垂直边缘（上下变化）


# 3. 卷积运算（用3×3窗口滑动计算边缘）
edge_x = np.zeros_like(img_array)  # 水平边缘结果
edge_y = np.zeros_like(img_array)  # 垂直边缘结果

# 遍历每个像素（跳过边缘，避免越界）
for i in range(1, height-1):
    for j in range(1, width-1):
        # 取3×3邻域
        patch = img_array[i-1:i+2, j-1:j+2]
        # 与Sobel算子卷积（点积求和）
        edge_x[i, j] = np.sum(patch * sobel_x)
        edge_y[i, j] = np.sum(patch * sobel_y)

# 合并水平和垂直边缘（取平方和开根号）
edge = np.sqrt(edge_x**2 + edge_y**2)
# 归一化到0-255（便于显示）
edge = (edge / edge.max() * 255).astype(np.uint8)


# 4. 显示原图和边缘图
plt.figure(figsize=(12, 6))
plt.subplot(121)
plt.imshow(img_array, cmap="gray")
plt.title("原图")
plt.subplot(122)
plt.imshow(edge, cmap="gray")
plt.title("边缘检测结果")
plt.show()

# 保存结果
Image.fromarray(edge).save("edge_result.jpg")

结果解读：

Sobel 算子通过卷积计算像素值的 “变化率”：变化大的区域（边缘）会被突出；
NumPy 的矩阵乘法（patch * sobel_x）和求和（np.sum）实现卷积，比 Python 循环快 10 倍以上；
结果图中，物体轮廓（如门窗、边框）被清晰提取，可用于图像识别预处理。

案例 6：机器学习特征选择（相关性分析）

场景：机器学习中特征过多会导致模型复杂，用 NumPy 计算特征与目标变量的相关性，筛选高相关特征，简化模型。

import numpy as np

# 1. 生成模拟数据（1000个样本，5个特征+1个目标变量）
np.random.seed(42)
n_samples = 1000
# 特征1-3与目标强相关，特征4-5与目标弱相关
X = np.random.randn(n_samples, 5)  # 5个特征
y = 2*X[:,0] + 1.5*X[:,1] - 3*X[:,2] + 0.1*np.random.randn(n_samples)  # 目标变量（依赖特征1-3）


# 2. 计算特征与目标的相关性（皮尔逊相关系数）
def corr_coef(x, y):
    """计算单个特征x与目标y的相关系数"""
    mean_x = np.mean(x)
    mean_y = np.mean(y)
    numerator = np.sum((x - mean_x) * (y - mean_y))
    denominator = np.sqrt(np.sum((x - mean_x)**2) * np.sum((y - mean_y)** 2))
    return numerator / denominator

# 计算每个特征与目标的相关性
corrs = np.array([corr_coef(X[:, i], y) for i in range(5)])
print("各特征与目标的相关系数：")
for i, corr in enumerate(corrs):
    print(f"特征{i+1}：{corr:.3f}")


# 3. 筛选高相关特征（阈值：绝对值>0.5）
high_corr_mask = np.abs(corrs) > 0.5
high_corr_features = X[:, high_corr_mask]  # 筛选后的特征

print(f"\n原始特征数：{X.shape[1]}，筛选后特征数：{high_corr_features.shape[1]}")
print("被选中的特征索引：", np.where(high_corr_mask)[0] + 1)  # 索引+1（从1开始）

结果解读：

皮尔逊相关系数范围 [-1,1]，绝对值越大，线性相关性越强；
特征 1-3 与目标的相关系数绝对值 > 0.5（强相关），被保留；特征 4-5 被剔除；
该方法可快速减少特征维度，提升模型训练速度，避免过拟合。

案例 7：科学计算（求解线性方程组）

场景：物理、工程中常遇到线性方程组（如电路电流、结构受力分析），用 NumPy 的线性代数模块快速求解。

import numpy as np

# 场景：一个简单电路，3个回路电流I1、I2、I3满足以下方程组（单位：A）
# 5I1 - 2I2 - 3I3 = 10
# -2I1 + 6I2 - 4I3 = 0
# -3I1 -4I2 + 10I3 = 0

# 1. 定义方程组（Ax = b）
A = np.array([
    [5, -2, -3],
    [-2, 6, -4],
    [-3, -4, 10]
])  # 系数矩阵
b = np.array([10, 0, 0])  # 常数项向量


# 2. 求解方程组（x = A⁻¹b）
# 方法1：用np.linalg.solve（推荐，更高效）
x = np.linalg.solve(A, b)

# 方法2：求逆矩阵后相乘（x = A_inv @ b）
A_inv = np.linalg.inv(A)
x_inv = A_inv @ b

print("方程组的解（电流，单位A）：")
print(f"I1 = {x[0]:.2f}，I2 = {x[1]:.2f}，I3 = {x[2]:.2f}")
print("两种方法结果是否一致：", np.allclose(x, x_inv))  # 验证结果


# 3. 验证解的正确性（代入原方程）
print("\n验证解是否满足方程：")
for i in range(3):
    lhs = np.sum(A[i] * x)  # 左边：A[i] @ x
    rhs = b[i]  # 右边：b[i]
    print(f"方程{i+1}：左边={lhs:.2f}，右边={rhs}（误差：{abs(lhs-rhs):.6f}）")

结果解读：

线性方程组Ax = b的解可通过np.linalg.solve(A, b)直接求得，比求逆矩阵（np.linalg.inv）更高效、数值更稳定；
验证结果显示，解代入原方程后误差接近 0，说明求解正确；
该方法可扩展到复杂场景（如 1000 个未知数的方程组），是工程计算的核心工具。

六、常见问题与避坑指南（新手必看）

修改切片影响原数组原因：NumPy 切片是原数组的视图（共享内存），不是副本。解决：用copy()方法创建副本，比如arr_slice = arr[2:5].copy()。
数据类型不匹配导致运算错误比如int数组和float数组运算后变成float，或整数除法结果为int（如3/2=1）。解决：运算前用astype统一类型，比如arr = arr.astype(np.float64)。
广播失败（形状不兼容）报错 “ValueError: operands could not be broadcast together”。解决：用reshape调整形状，使其满足广播规则，比如把 (3,) 数组改成 (1,3) 再和 (2,3) 数组运算。
内存不足（处理超大数组）原因：NumPy 数组存储在连续内存中，超大数组（如 10GB）可能耗尽内存。解决：分块处理（用np.array_split拆分），或用memmap创建内存映射文件（不一次性加载到内存）。
混淆轴的方向（axis 参数）2 维数组中，axis=0是按列运算，axis=1是按行运算，新手容易搞反。记忆法：axis=0是 “垂直方向”（从上到下），axis=1是 “水平方向”（从左到右）。

七、学习资源与进阶方向（持续提升）

1. 免费学习资源

官方文档：https://numpy.org/doc/stable/ （最权威，包含详细教程和函数说明）；
NumPy 中文教程：https://www.numpy.org.cn/ （适合英文不好的新手）；
练习平台：Kaggle（https://www.kaggle.com/）提供大量数据集，可练手 NumPy 数据处理。

2. 进阶方向

线性代数：NumPy 的linalg模块（np.linalg.inv求逆矩阵、np.linalg.eig求特征值），是机器学习的基础；
性能优化：用numba库给 NumPy 代码加速（可接近 C 语言速度），或用Cython编写扩展；
并行计算：结合Dask处理超大数据集（超过内存的数据集），实现并行运算；
与其他库结合：Pandas 数据清洗、Matplotlib 可视化、Scikit-learn 机器学习，都需要 NumPy 基础。

总结：NumPy 的核心价值与学习建议

NumPy 不是一个 “可有可无” 的库，而是 Python 数据科学的 “基础设施”—— 它用 C 语言的速度和 Python 的简洁，解决了 “大量数值计算效率低” 的痛点。学会 NumPy，不仅能提升代码效率，更能理解 “向量化思维”：用数组操作替代循环，用数学运算描述逻辑，这是数据分析和机器学习的核心思维方式。

对于新手，我的学习建议是：