数据结构——“图”的相关知识总结

最新推荐文章于 2024-05-04 21:30:02 发布

拥抱@

最新推荐文章于 2024-05-04 21:30:02 发布

阅读量4.2k

点赞数 3

CC 4.0 BY-SA版权

分类专栏： Data Structure 文章标签：图

本文链接：https://blog.youkuaiyun.com/tonglin12138/article/details/95537644

Data Structure 专栏收录该内容

17 篇文章

订阅专栏

本文介绍了图这种数据结构，包括基本概念，如顶点、边、有向图、无向图等；存储结构，如邻接矩阵和邻接表；以及遍历方法，如广度优先遍历和深度优先遍历。详细阐述了各部分的定义、特点及代码实现思路。

1. 图的基本概念

图是由顶点集合及顶点间的关系组成的一种数据结构：G = (V， E)，其中：顶点集合

V = {x|x属于某个数据对象集}是有穷非空集合；
E = {(x,y)|x,y属于V}或者E = {<x, y>|x,y属于V && Path(x, y)}是顶点间关系的有穷集合，也叫做边的集合。

(x, y)表示x到y的一条双向通路，即(x, y)是无方向的；
Path(x, y)表示从x到y的一条单向通路，即Path(x, y)是有方向的。

顶点和边：图中结点称为顶点，第i个顶点记作vi。两个顶点vi和vj相关联称作顶点vi和顶点vj之间有一条边，图中的第k条边记作ek，ek = (vi，vj)或<vi，vj>。

有向图和无向图：在有向图中，顶点对<x, y>是有序的，顶点对<x，y>称为顶点x到顶点y的一条边(弧)，<x,y>和<y, x>是两条不同的边，比如下图G3和G4为有向图。在无向图中，顶点对(x, y)是无序的，顶点对(x,y)称为顶点x和顶点y相关联的一条边，这条边没有特定方向，(x, y)和(y，x)是同一条边，比如下图G1和G2为无向图。注意：无向边(x, y)等于有向边<x, y>和<y, x>。

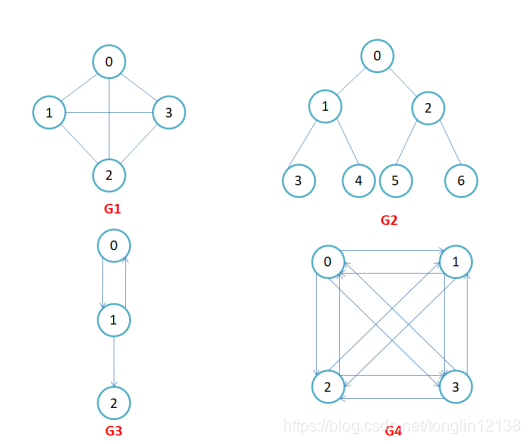
在这里插入图片描述
完全图：在有n个顶点的无向图中，若有n * (n-1)/2条边，即任意两个顶点之间有且仅有一条边，则称此图为无向完全图，比如上图G1；
在n个顶点的有向图中，若有n * (n-1)条边，即任意两个顶点之间有且仅有方向
相反的边，则称此图为有向完全图，比如上图G4。

邻接顶点：在无向图中G中，若(u, v)是E(G)中的一条边，则称u和v互为邻接顶点，并称边(u,v)依附于顶点u和v；在有向图G中，若<u, v>是E(G)中的一条边，则称顶点u邻接到v，顶点v邻接自顶点u，并称边<u, v>与顶点u和顶点v相关联。

顶点的度：顶点v的度是指与它相关联的边的条数，记作deg(v)。在有向图中，顶点的度等于该顶点的入度与出度之和，其中顶点v的入度是以v为终点的有向边的条数，记作indev(v);顶点v的出度是以v为起始点的有向边的条数，记作outdev(v)。因此：dev(v) = indev(v) + outdev(v)。
注意：对于无向图，顶点的度等于该顶点的入度和出度，即dev(v) = indev(v) = outdev(v)。

路径：在图G = (V， E)中，若从顶点vi出发有一组边使其可到达顶点vj，则称顶点vi到顶点vj的顶点序列为从顶点vi到顶点vj的路径。
路径长度：对于不带权的图，一条路径的路径长度是指该路径上的边的条数；对于带权的图，一条路径的路径长度是指该路径上各个边权值的总和。
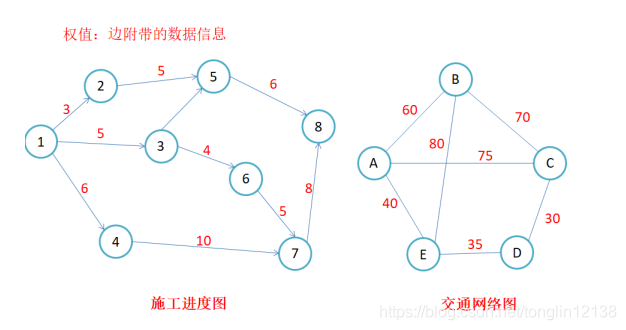
在这里插入图片描述
简单路径与回路：若路径上各顶点v1，v2，v3，…，vm均不重复，则称这样的路径为简单路径。若路径上第一个顶点v1和最后一个顶点vm重合，则称这样的路径为回路或环。

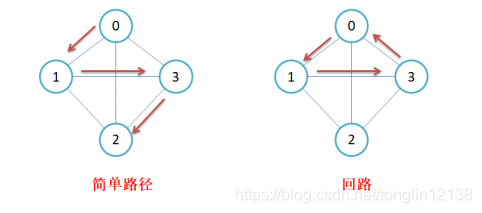
在这里插入图片描述
子图：设图G = {V, E}和图G1 = {V1，E1}，若V1属于V且E1属于E，则称G1是G的子图。

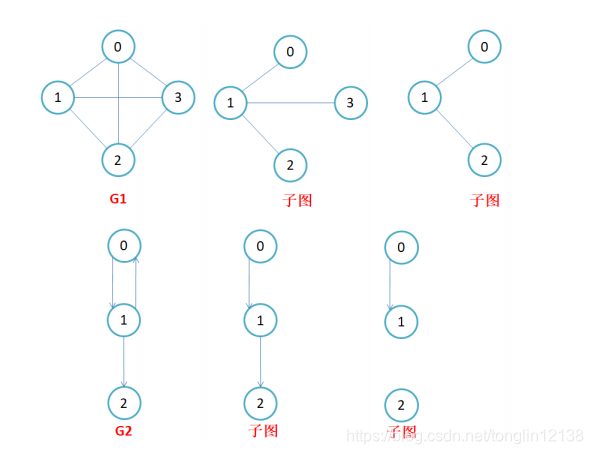
在这里插入图片描述
连通图：在无向图中，若从顶点v1到顶点v2有路径，则称顶点v1与顶点v2是连通的。如果图中任意一对顶点都是连通的，则称此图为连通图。

强连通图：在有向图中，若在每一对顶点vi和vj之间都存在一条从vi到vj的路径，也存在一条从vj到 vi的路径，则称此图是强连通图。

生成树：一个连通图的最小连通子图称作该图的生成树。有n个顶点的连通图的生成树有n个顶点和n- 1条边。

2. 图的存储结构

因为图中既有节点，又有边(节点与节点之间的关系)，因此，在图的存储中，只需要保存：节点和边关系即可。节点保存比较简单，只需要一段连续空间即可，那边关系该怎么保存呢？

邻接矩阵
因为节点与节点之间的关系就是连通与否，即为0或者1，因此邻接矩阵(二维数组)即是：先用一个数组将定点保存，然后采用矩阵来表示节点与节点之间的关系。

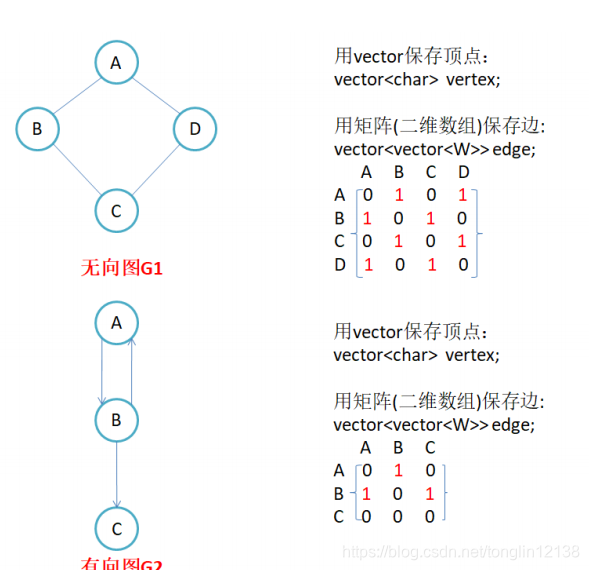
注意：
无向图的邻接矩阵是对称的，第i行(列)元素之和，就是顶点i的度。有向图的邻接矩阵则不一定是对称的，第i行(列)元素之后就是顶点i 的出(入)度。
如果边带有权值，并且两个节点之间是连通的，上图中的边的关系就用权值代替，如果两个顶点不通，则使用无穷大代替。

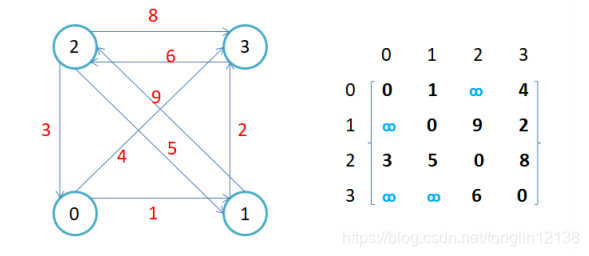
用邻接矩阵存储图的有点是能够快速知道两个顶点是否连通，缺陷是如果顶点比较多，边比较少时，矩阵中存储了大量的0成为系数矩阵，比较浪费空间，并且要求两个节点之间的路径不是很好求。

代码：

#pragma once
#include <vector>
#include <iostream>
using namespace std;
#include <assert.h>


// V---> 顶点的类型
// W---> 边所对应权值的类型
// IsDirect: false-->无向图  true--->有向图
template<class V, class W, bool IsDirect = false>
class Graph
{
public:
	Graph(const V* pv, size_t N, const W& invalid)
		: _vertex(pv, pv+N)
		, _invalidWeight(invalid)
	{
		// 1. 将顶点添加到图中
		// 2. 将保存边的矩阵初始

		// 二维数组行数
		_edges.resize(N);
		for (size_t i = 0; i < N; ++i)
			_edges[i].resize(N, invalid);
	}

	size_t GetIndexOfVertex(const V& v)
	{
		for (size_t index = 0; index < _vertex.size(); ++index)
		{
			if (_vertex[index] == v)
				return index;
		}

		assert(false);
		return -1;
	}

	void AddEdge(const V& v1, const V& v2, const W& weight)
	{
		// 获取v1和v2顶点在顶点集合中的下标
		size_t srcIdx = GetIndexOfVertex(v1);
		size_t dstIdx = GetIndexOfVertex(v2);

		if (srcIdx == dstIdx)
			return;

		_edges[srcIdx][dstIdx] = weight;
	
		//如果是无向图，则A-B，对应的B-A的权值也应该更新
		if (!IsDirect)
			_edges[dstIdx][srcIdx] = weight;
	}

	size_t GetDevOfVertex(const V& v)
	{
		size_t devCount = 0;
		size_t vIdx = GetIndexOfVertex(v);
		size_t N = _vertex.size();

		// 出度
		for (size_t i = 0; i < N; ++i)
		{
			if (_edges[vIdx][i] != _invalidWeight)
				devCount++;
		}

		if (IsDirect)
		{
			// 入度
			for (size_t i = 0; i < N; ++i)
			{
				if (_edges[i][vIdx] != _invalidWeight)
					devCount++;
			}
		}

		return devCount;
	}

	void PrintGraph()
	{
		// 打印顶点
		for (auto e : _vertex)
			cout << e << "  ";
		cout << endl;

		// 打印矩阵中的内容
		size_t N = _vertex.size();
		for (size_t i = 0; i < N; ++i)
		{
			for (size_t j = 0; j < N; ++j)
			{
				cout << _edges[i][j] << " ";
			}
			cout << endl;
		}
		cout << endl;
	}
private:
	std::vector<V> _vertex;
	std::vector<vector<W>> _edges;
	W _invalidWeight;
};


/*
测试用例：
"ABCDE"
'A', 'D' , 10
'A', 'E' , 20
'B', 'C' , 10
'B', 'D' , 20
'B', 'E' , 30
'C', 'E' , 40
*/

void TestGraph()
{
	char* pstr = "ABCDE";
	Graph<char, int, true> g(pstr, strlen(pstr), -1);
	g.AddEdge('A', 'D', 10);
	g.AddEdge('A', 'E', 20);
	g.AddEdge('B', 'C', 10);
	g.AddEdge('B', 'D', 20);
	g.AddEdge('B', 'E', 30);
	g.AddEdge('C', 'E', 40);

	g.PrintGraph();
	cout << g.GetDevOfVertex('E') << endl;
}

邻接表
邻接表：使用数组表示顶点的集合，使用链表表示边的关系。

1.无向图邻接表存储
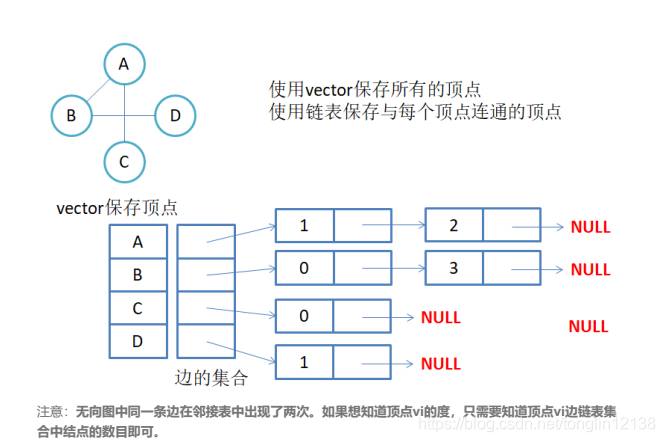
在这里插入图片描述
2.有向图邻接表存储

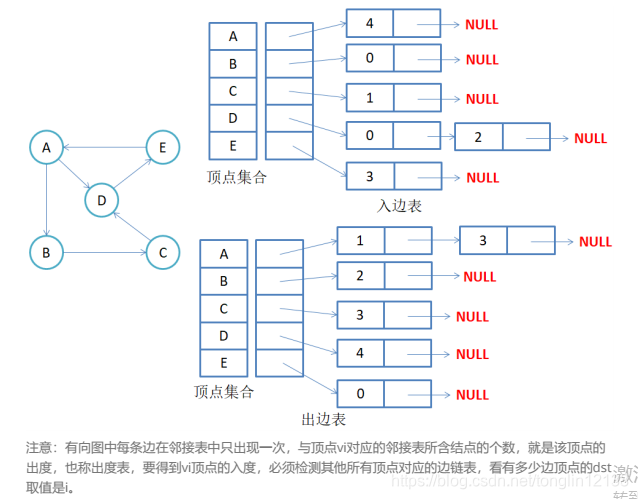
代码实现：

template<class W>p
struct LinkEdge
{
LinkEdge<W>* _pNext;
W _weight; // 节点的权值
size_t _src; // 起点的下标(后面使用)
size_t _dst; // 终点的下标
LinkEdge(size_t src, size_t dst, const W& weight)
: _src(src)
, _dst(dst)
, _weight(weight)
, _pNext(NULL)
{}
};

template<class V, class W, bool IsDirect = false>
class Graph
{
	typedef LinkEdge<W> LinkEdge;
	typedef Graph<V, W, IsDirect> Self;
public:
	Graph(const V* array, size_t size)
	: _v(array, array+size)
{
	_linkEdges.resize(size);
}

// g.AddEdge('A', 'D', 10);
void AddEdge(const V& v1, const V& v2, const W& weight)
{
	size_t src = GetIndexOfV(v1);
	size_t dst = GetIndexOfV(v2);
	_AddEdge(src, dst, weight);
	if(!IsDirect)
	_AddEdge(dst, src, weight);
}

// 获取顶点元素在其数组中的下标
	size_t GetIndexOfV(const V& v)
{
	for(size_t i = 0; i < _v.size(); ++i)
{
	if(v == _v[i])
	return i;
}

	assert(false);
	return -1;
}

void PrintGraph()
{
for(size_t index = 0; index < _v.size(); ++index)
{
	cout<<"v["<<_v[index]<<"]--->";
	LinkEdge* pCur = _linkEdges[index];
	while(pCur)
{
	cout<<"v["<<_v[pCur->_dst]<<"]--->";
	pCur = pCur->_pNext;
}
	cout<<"NULL"<<endl;
}
}

//获取节点的度
int GetVDev(const V& v)
{
	size_t index = GetIndexOfV(v);	
	LinkEdge* pCur =_linkEdges[index];
	size_t count = 0;
// 出度
while(pCur)
{
  count++;
  pCur = pCur->_pNext;
}

if(IsDirect)
{
// 入度
	int dst = index;
	for(size_t src = 0; src < _v.size(); ++src)
{
	if(src == dst)
	 continue;
	else
{
	LinkEdge* pCur = _linkEdges[src];
	while(pCur)
{
 	if(pCur->_dst == dst)
	count++;
	pCur = pCur->_pNext;
}
}

}
}
	return count;
}


void _AddEdge(size_t src, size_t dst, const W& weight)
{
	LinkEdge* pCur = _linkEdges[src];
	// 检测当前边是否存在
	while(pCur)
	{
	if(pCur->_dst == dst)
	   return;
	pCur = pCur->_pNext;
}
	//头插
	LinkEdge* pNewNode = new LinkEdge(src, dst, weight);
	pNewNode->_pNext = _linkEdges[src];
	_linkEdges[src] = pNewNode;
}

private:
	vector<V> _v;
	vector<LinkEdge*> _linkEdges;
};

3.图的遍历

1.广度优先遍历

类比二叉树的层序遍历；

void level_order(Bitree *root)
{
 
  if(root==NULL)
     return;
  
  Bitree p=root;
  queue<Bitree>queue_;
  queue.push(p);
  while(!queue_.empty())
  {
     
     p=queue_.front();
     cout<<p->data<<endl;
     queue_.pop();    
     if(p->lchild)
     queue_.push(p->lchild);
     if(p->rchild)
     queue_.push(p->rchild);
 
}

}

图的广度优先遍历

_BFS(queue<int>& q,vector<bool>& visted){


while(!q.empty()){
size_t index=q.front;
if(!visted[index])  //如果该节点没有遍历过
{
   cout<<_v[index]<<":";
   visted[index]=true;
   LinkEdge* pCur = _linkEdges[index];
   while(pCur)
  {
    q.push(pCur->_dst);
    pCur = pCur->_pNext;
}
}
	q.pop();

}
	cout<<endl;
}


void BFS(const V& v){
	queue<int>q;
	vector<bool>_visted(_v.size(),false);
	q.push(GetIndex(v));
	_BFS(q,_visted);
	
}

2.深度优先遍历
类比二叉树的先序遍历

1 void preOrder1(BinTree *root)     //递归前序遍历 
2 {
3     if(root!=NULL)
4     {
5         cout<<root->data<<" ";
6         preOrder1(root->lchild);
7         preOrder1(root->rchild);
8     }
9 }

图的深度遍历


void _DFS(int index, vector<bool>& visited)
{
	if(!visited[index])
 {
	cout<<_v[index]<<" ";
	visited[index] = true;
	LinkEdge* pCur = _linkEdges[index];
	while(pCur)
	{
		_DFS(pCur->_dst, visited);
		pCur = pCur->_pNext;
	}
 }
}

void DFS(const V& v)
{
	cout<<"DFS:";
	vector<bool> visited(_v.size(), false);
	_DFS(GetIndexOfV(v), visited);

	for(size_t index = 0; index < _v.size(); ++index)
	_DFS(index, visited);
	cout<<endl;