快速排序算法

博客参考了《啊哈！算法》和y总的算法基础课。

时间复杂度：最差：O（N^2） 平均：O(N*logN)

空间复杂度：

  （一）思路

大体思路

         1.取分界点（基准数）

                高位和低位相遇的点

         2.分成两部分，左小右大

              达到以基准数为中心，左边小于基准数，右边大于基准数。

         3.各自排大小，选取基准数

               将左右两边各自排序，最后结合在一起。

          4.确定结果

                选出的基准数排列即为结果

详细步骤

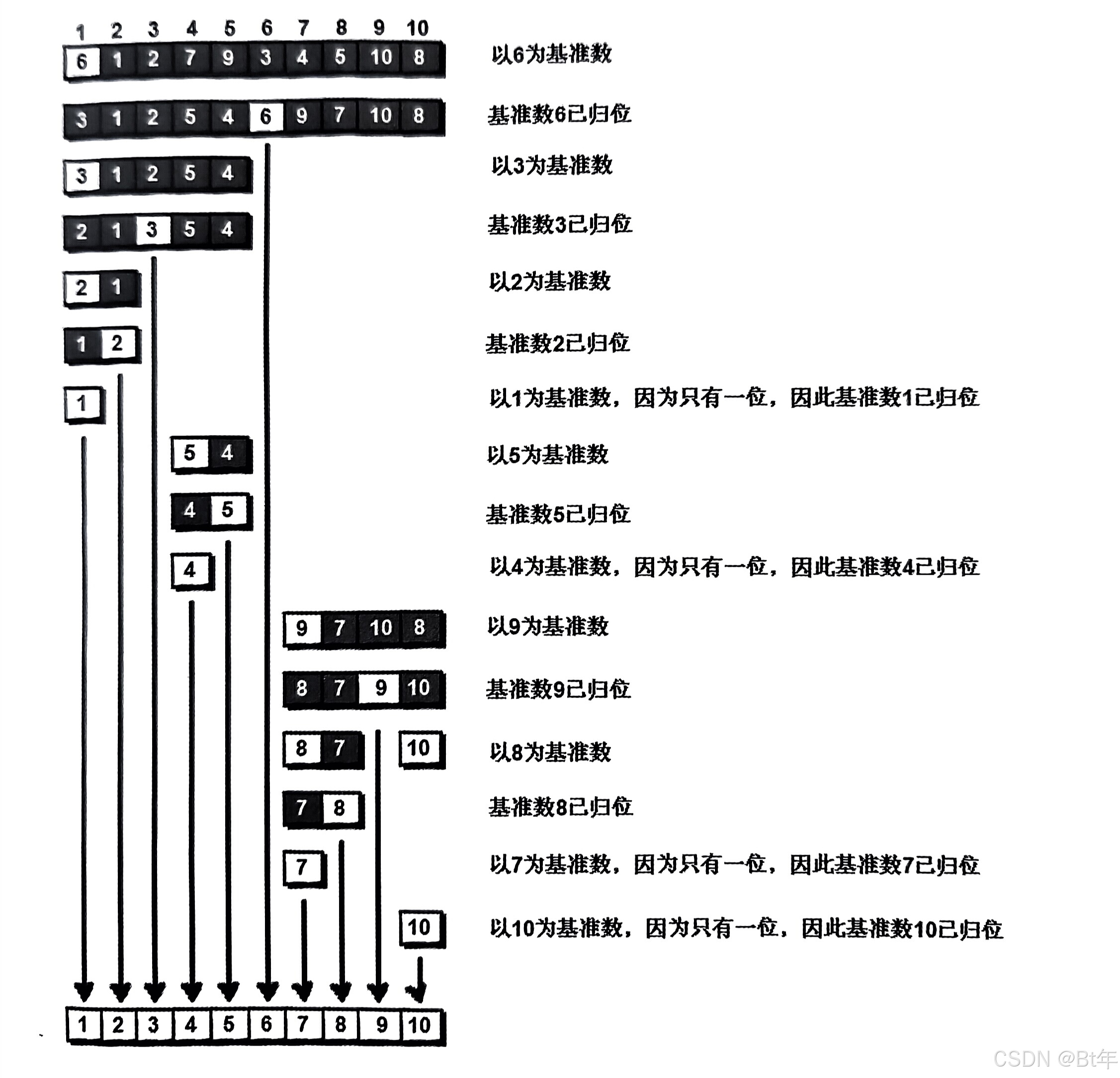
        例题：“6 1 2 7 9 3 4 5 10 8”

                初始状态下，一般选择最左端6为基准点（注意真实情况下基准点点选择并不是谁便选的，要尽量保证排序后左右数量尽量相等），先从右向左选择小于6（能不能从左向右？为什么？）5，再从左向右选择一个大于6的数7，然后交换它们，从左端出发的为变量i，从右端出发的为变量j。

while(i!=j)
{
    //temp为基准数。
    //先从右向左（很重要），选择小于基准数的数
    while(a[j]>=temp &&)i<j)
        j--;
    //从左向右，选择大于基准数的数
    while(a[i]<=temp &&i<j)
        i++;
    
    if(i<j)// i和j没有相遇
    {
        t=a[i];
        a[i]=a[j];
        a[j]=t;
    }
}

         当i和j相遇时，交换基准数与这个相遇数，注意i和j只是变量，不交换它们。自此第一轮结束？（3 1 2 5 4 6 9 7 10 8）

        由于基准数的初始位置在左边，所以相遇数一定要小于基准数，那么怎么保证相遇的数一定比基准数小呢？

        结合为什么先从右往左的问题，每次交换后都是先从右向左选择小于基准数的，故最后相遇的数肯定小于基准数。

接下来以6为分解点，分成左右两个部分，各自重复上边的操作。如图所示（来源《啊哈！算法》）

   （二）问题

             1.分界点怎么选择？只能选择最左边嘛？

                        不是，基准数可以取在任意地方。

   （三）代码

C++(快排函数实现)

#include <iostream>
using namespace std;

void QuickSort(int *arr,int l,int r)
{
	if(l>=r) return;
	
	int point=arr[l],i=l-1,j=r+1;
	while(i<j)
	{
		do i++; while(arr[i]<point);
		do j--; while(arr[j]>point);
		if(i<j)swap(arr[i],arr[j]);
	}
	QuickSort(arr,l,j);
	QuickSort(arr,j+1,r);
}

int main()
{
	int arr[]={1,5,6,7,9,2,4};
	QuickSort(arr,0,sizeof(arr)/sizeof(int)-1);
	for (int i = 0; i < sizeof(arr)/sizeof(int); i++) 
	{
		cout << arr[i] << " ";
	}
	return 0;	
}

C （自定义函数实现）

#include<stdio.h>

int a[101],n;//定义全局变量，这两个变量需要在子函数中使用

void quicksort(int left,int right)
{
    int i,j,t,temp;

    if(left > right )
    return;

    temp = a[left]
    i=left;
    j=right;
    
    while(i!=j)
    {
        //temp为基准数。
        //先从右向左（很重要），选择小于基准数的数
        while(a[j]>=temp &&)i<j)
            j--;
        //从左向右，选择大于基准数的数
        while(a[i]<=temp &&i<j)
            i++;
    
        if(i<j)// i和j没有相遇
        {
            t=a[i];
            a[i]=a[j];
            a[j]=t;
        }
    }
    //最终将基准数归位。

    a[left]=a[i];
    a[i]=temp;

    quicksort(left,i-1);
    quicksort(i+1,right);
    return ;
    
}

int main()
{
    int i,j;
    //读入数据
    scanf("%d",&n);
    for(i=1 ; i<=n ;i++)
        scanf("%d",&a[i]);

    quicksort(1,n); //快速排序调用

    //输出排序后的结果
    for(i=1 ; i<=n ;i++)
        printf("%d",a[i]);

    getchar();getchar();

    return 0;
}

例题（sort函数）

        sort可以用来对结构体数组进行排序，这取决于它的第三个参数：sort(begin, end, cmp)；我们直接看一道题：L2-003 月饼 - 团体程序设计天梯赛-练习集

        代码：

#include<bits/stdc++.h>
using namespace std;
typedef struct 
{
    double Price;//总价
    double inventory;//库存
    double unval;
}moon;
bool cmp(const moon&a,const moon&b)
{
    return a.unval>b.unval;
}
int main()
{
    int n;
    double num;
    double sum=0.00;
    scanf("%d%lf",&n,&num);
    moon *Mooncakes=new moon[n];
    for (int i = 0; i < n; i++)
        scanf("%lf",&Mooncakes[i].inventory);    
    for (int i = 0; i < n; i++)
    {
        scanf("%lf",&Mooncakes[i].Price);
        Mooncakes[i].unval=(double)Mooncakes[i].Price/(double)Mooncakes[i].inventory;
    }  
    sort(Mooncakes,Mooncakes+n,cmp);//按单价由大到小排序  
    for(int i=0;num!=0&&i<n;i++)
    {
        if(Mooncakes[i].inventory<=num)
        {
            num-=Mooncakes[i].inventory;
            sum+=Mooncakes[i].Price;
        }
        else
        {
            sum+=num*Mooncakes[i].unval;
            num=0;
        }
    }
    printf("%0.2lf\n",sum);
}