决策树简介

3.1 决策树简介
优点：计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据。
缺点：可能会产生过度匹配问题。
适用数据类型：数值型和标称型。

3.2 决策树的一般流程
(1) 收集数据：可以使用任何方法。
(2) 准备数据：树构造算法只适用于标称型数据，因此数值型数据必须离散化。
(3) 分析数据：可以使用任何方法，构造树完成之后，应该检查图形是否符合预期。
(4) 训练算法：构造树的数据结构。
(5) 测试算法：使用经验树计算错误率。
(6) 使用算法：此步骤适用于任何监督学习算法，使用决策树可以更好地理解数据的内在含义。

3.3 决策树的构造

(1) 信息增益

划分数据集的大原则：将无序的数据变得更加有序。

组织杂乱无章数据的一种方法就是使用信息论度量信息，信息论是量化处理信息的分支科学。

信息增益：在划分数据集之前之后信息发生的变化，获得信息增益最高的特征就是最好的选择。

熵：集合信息的度量方式称为香农熵或者简称为熵。熵定义为信息的期望值。

信息：如果待分类的事务可能划分在多个分类之中，则xi的信息定义为：

其中，p(xi)是选择该分类的概率。

所有类别所有可能值包含的信息期望值：

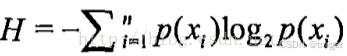其中，n是分类的数目。

熵代表信息的混乱度信息。其基本作用就是消除人们对事物的不确定性。一个系统越是有序，信息熵就越低；反之，一个系统越是混乱，信息熵就越高。所以，信息熵也可以说是系统有序程度的一个度量。

(2)  划分数据集

对每个特征划分数据集的结果计算一次信息熵，判断按照哪个特征划分数据集是最好的划分方式。

(3)  递归构建决策树

工作原理：得到原始数据集，基于最好的属性值划分数据集，第一次划分后，再次划分数据。因此可以递归处理数据集。

递归结束的条件：划分数据集所有属性，或者每个分支下的所有实例都具有相同的分类。