定义
正向运动学:描述的是由机器人的关节空间到笛卡尔空间的映射。
通俗的说就是知道机器人n个关节角度得到机器人末端执行器的三维姿态信息与三维位置坐标,
以后简称六维位姿(6D位姿)。
为什么需要姿态信息呢,因为在抓取,采摘等复杂认为在,以何种姿态完成任务影响任务成败。
两种形式
DH参数
DH参数是一种应用非常广泛的正运动建模方式。
优点是:可以用较少的参数描述正运动学。
缺点是:对每个轴都需要建立坐标系。非常麻烦。
下面以franka机器人为例
结构如下

需要先建立DH参数表如下

再通过如下公式建立其次矩阵:

最后
T
=
T
1
∗
T
2
.
.
.
.
.
.
.
∗
T
n
T=T_1*T_2.......*T_n
T=T1∗T2.......∗Tn
得到正运动学的映射,可以看出有点麻烦,但是在动力学建模时,DH参数非常重要,运动学没必要使用这样麻烦的建模。使用PoE更加方便。
PoE
PoE的建模过程非常简单,只需要定义两个坐标系即可。即基座标系和末端坐标系。下面只介绍具体操作,不涉及理论(理论见《现代机器人学》P86)。
还是以Franka机器人为例
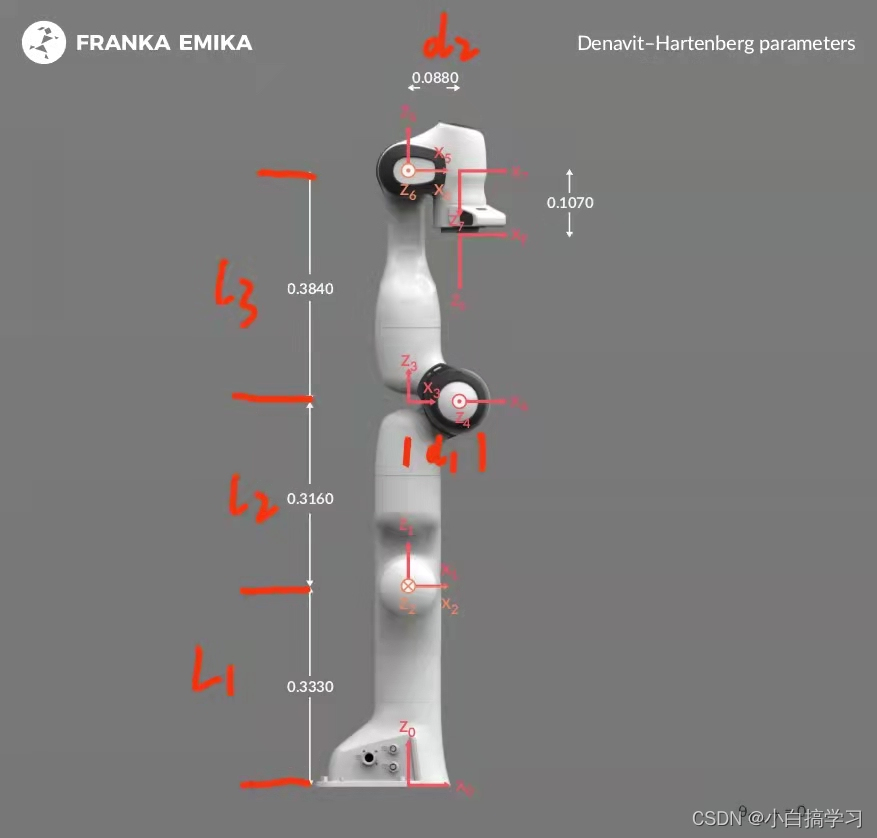
首先,构建初始位形
M=[[1,0,0,d2],
[0,-1,0,0],
[0,0,-1,L1+L2+L3-L4],
[0,0,0,1]]
这里实际上只需要
x
0
y
0
z
0
x_0y_0z_0
x0y0z0和
x
f
y
f
z
f
x_fy_fz_f
xfyfzf两个坐标系和每个转轴的转动方向即可。
以1号轴为例
w
1
=
(
0
,
0
,
1
)
,
q
1
=
(
0
,
0
,
L
1
)
w_1=(0,0,1),q_1=(0,0,L_1)
w1=(0,0,1),q1=(0,0,L1),其中
q
q
q是转轴上的任一一点,再通过
v
1
=
w
1
×
q
1
v_1=w_1\times q_1
v1=w1×q1 计算
v
v
v.
需要注意的是:可以取转轴上面的任一点,因为转轴上的量叉乘之后会是0,不影响
v
v
v.
如第4轴,转轴方向是y方向,则
q
4
q_4
q4在y轴上面取值可以随意,叉乘出来并不影响,但是
x
x
x与
z
z
z方向不能随意取值
| w | q |
|---|---|
| (0,0,1) | (0,0, L 1 L_1 L1) |
| (0,1,0) | (0,0, L 1 L_1 L1) |
| (0,0,1) | (0,0, L 1 + L 2 L_1+L_2 L1+L2) |
| (0,-1,0) | ( d 1 d_1 d1,0, L 1 + L 2 L_1+L_2 L1+L2) |
| (0,0,1) | (0,0, L 1 + L 2 + L 3 L_1+L_2+L_3 L1+L2+L3) |
| (0,-1,0) | (0,0, L 1 + L 2 + L 3 L_1+L_2+L_3 L1+L2+L3) |
| (0,0,-1) | ( d 2 d_2 d2,0, L 1 + L 2 + L 3 L_1+L_2+L_3 L1+L2+L3) |
再通过 v 1 = w 1 × q 1 v_1=w_1\times q_1 v1=w1×q1 计算 v v v. S l i s t = ( w , v ) Slist=(w,v) Slist=(w,v)即组成了关节旋量。
Slist=np.array([[0,0,1,-0.,-0.,-0.],
[0,1,0,-0.333,-0.,-0.],
[0,0,1,-0.,-0.,-0.],
[0,-1,0,0.649,-0.,-0.082],
[0,0,1,-0.,-0.,-0.],
[0, -1, 0, 1.033, -0., -0.],
[0,0,-1,-0.,0.088,-0.]]);
至此建模完成,最后通过
T_end=mr.FKinSpace(M, Slist.T, thetalist)
计算出对应角度
t
h
e
t
a
l
i
s
t
thetalist
thetalist下的位姿
T
e
n
d
T_{end}
Tend。这个函数是《现代机器人学》一书中对应的代码库可以通过下面链接下载
代码库
























 5978
5978

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?








