C语言复习（五）—— 运算符

一个函数的构成
：返回类型 函数名（形参列表）

C语言运算符的优先级表

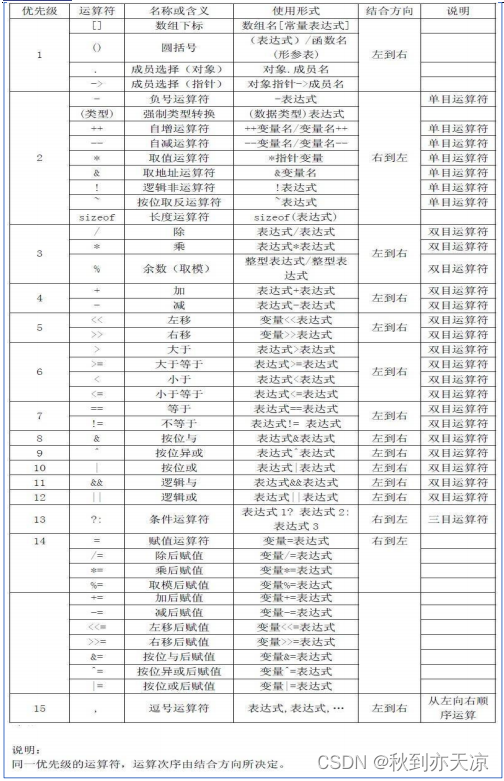
在讲解具体运算符之前，介绍几个与之相关的术语：
操作数（operand）、运算符（operator）、左值（lvalue）和右值（rvalue）。

**操作数（operand）**是程序操纵的数据实体，该数据可以是数值、逻辑值或其他类型。该操作数既可以是常量也可以为变量。

运算符（operator）是可以对数据进行相应操作的符号。如对数据求和操作，用加法运算符 ‘+’，求积操作使用乘法运算符 ‘*’ 等。

根据运算符可操作的操作数的个数，可把运算符分为一元运算符（单目运算符）、二元运算符（双目运算符）和多
元运算符（C 语言只有一个三元运算符（？：），三目运算符）。

C 语言提供了丰富的运算符：
有：算术运算符、关系运算符、逻辑运算符、赋值运算符、移位运算符、逗号运算符及 sizeof 运算符。

对应有：算术表达式、关系表达式、逻辑表达式、赋值表达式、移位表达式、逗号表达式及 sizeof 表达式等。

左值（lvalue）和右值（rvalue）按字面意思通俗地说。
以赋值符号=为界，=左边的就是左值，=右边就是右值。

更深一层，可以将 L-value 的 L, 理解成 Location，表示可寻址。Avalue (computer science)that has an address 。R-value 中的 R 指的是 Read，表示可读。in computer science, a value that does not have an address in a computer language.

---

运算符举例

1. % (余数)取模
2. *=， +=
3. 三目运算符
4. 主要讲解前置++，和后置++；

1.余数的定义：整除“余”下的“数”。
则有：余数＝被除数－商*除数
商就是我们整除的结果。

取模运算在 c 语言中的应用：

1、判断是否能够整除某个数;
2、判别奇偶数，判别质数（或素数）;
3、计算范围。形成循环。
4、求最大公约数; 求最大公约数最常见的方法是欧几里德算法（又称辗转相除法），
其计算原理依赖于定理：gcd(a,b) = gcd(b,a mod b)

辗转相除法的原理：

a/b=q余r，除数b和余数r能被同一个数整除，那么被除数a也能被这个数整除。或者说，除数与余数的最大公约数，就是被除数与除数的最大公约数。即被除数与除数的最大公约数，就是除数与余数的最大公约数

#include <stdio.h>
 
int main()
{
	int m = 0;
	int n = 0;
	scanf("%d %d", &m, &n);	
	int r = 0;
	while (r = m % n)
	{
		m = n; // 以除数作为被除数
		n = r; // 以余数作为除数
	}
	printf("%d\n", n); // 最后的除数为最大公约数
	return 0;
}

由于被除数与除数的最大公约数，就是除数与余数的最大公约数，即gcd(a,b)=gcd(b, a%b)，所以也可以设计一个递归算法计算最大公约数。

#include <stdio.h>
 
int gcd(int a, int b)
{
	if (b == 0)
		return a;
	else
		return gcd(b, a % b);
}
 
int main()
{
	int m = 0;
	int n = 0;
	scanf("%d %d", &m, &n);
	printf("%d\n", gcd(m, n));
	return 0;
}

1.取模

2.运算符顺序

#include<stdio.h>
#include<stdlib.h>

 int main()
{
 int a = 3, b = 4, c = 5;
 a *= b + c;//(从右往左计算)
 printf("a = %d \n",a); a =27
return 0;
}

#include<stdio.h>
void main()
{
	int a=1,b=2,c=3,d,e;
	d=((c>a)?a:b);
	e=((c<a)?a:b);
	printf("d=%d,e=%d\n",d,e);
}
 
输出：d=1，e=2