机器学习详解(12):归一化和标准化

数据对于模型性能和结果解释至关重要，这就是归一化(Normalization)和标准化(Standardization)这两种两种用于特征缩放的方法发挥作用的地方。

本篇文章将详细介绍归一化和标准化的概念，比较它们的实际差异，并说明在数据预处理中何时使用它们。通过掌握这些方法，你可以提升模型性能，更清晰地解释结果，并避免未缩放数据带来的常见问题。

1 理解特征缩放

特征缩放通过将特征值转换为相似的尺度，确保它们在模型学习过程中有相同的贡献。对于特征在尺度上差异较大的情况，特征缩放显得尤为重要。

例如：

• 一个特征的取值范围是 1 到 10；
• 另一个特征的取值范围是 1000 到 10000。

如果没有缩放，模型可能会优先考虑较大的值，导致预测出现偏差。这可能会引发以下问题：

• 模型性能不佳；
• 训练收敛速度较慢。

为什么特征缩放很重要？

特征缩放可以：

• 平衡特征的重要性；
• 减少异常值的影响；
• 在某些情况下，加速模型收敛速度。

2 归一化

归一化是一个广泛的概念，指的是将不同尺度上的值调整到一个共同的尺度。以下是几种主要的归一化方法及其应用场景：

2.1 最小-最大归一化（Min-Max Normalization）

公式：

$$x^{\prime }=\frac{x-x_{\text{min}}}{x_{\text{max}}-x_{\text{min}}}$$

其中：

• $x$ 为原始值
• $x_{\text{min}}$ 和 $x_{\text{max}}$ 分别为特征的最小值和最大值
• $x^{\prime }$ 为归一化后的值

例子：
将房屋面积的最小值表示为 $0$，最大值表示为 $1$，房屋面积在此范围内按比例缩放。

优点：

• 简单直观，易于实现。
• 适用于范围已知的数据。
• 可以保持原始数据的分布形状。

2.2 对数归一化（Log Normalization）

公式：

$$x^{\prime }=\log (x+1)$$

其中：

• $x$ 为原始值
• $x^{\prime }$ 为归一化后的值
• 加 $1$ 是为了避免 $x=0$ 时无法取对数的问题

例子：

对房价应用对数变换，以减少高价房屋对模型的影响，尤其是在房价差异显著的情况下。

优点：

• 可以有效处理偏态分布的数据。
• 降低异常值对模型的影响。

2.3 小数缩放（Decimal Scaling）

公式：

$$x^{\prime }=\frac{x}{10^j}$$

其中：

• $j=\lceil {\log }_{10}(\max (|x|))\rceil$，为确保数据范围位于 $[-1,1]$ 内的最小整数
• $x$ 为原始值
• $x^{\prime }$ 为归一化后的值

例子：

将房屋面积通过移动小数点调整为更易处理的范围，例如 $1500$ 平方英尺变为 $1.5$。

优点：

• 简单直观，计算效率高。
• 保持数据的相对差异，易于解释。

2.4 均值归一化（Mean Normalization）

公式：

$$x^{\prime }=\frac{x-\mu }{x_{\text{max}}-x_{\text{min}}}$$

其中：

• $\mu$ 为特征的均值
• $x_{\text{min}}$ 和 $x_{\text{max}}$ 分别为特征的最小值和最大值
• $x^{\prime }$ 为归一化后的值

例子：

通过均值归一化调整房价数据，观察哪些房价高于或低于平均值。

优点：

• 便于分析数据相对于平均值的偏差。
• 保持数据的相对大小，适用于大多数线性模型。

2.5 零均值归一化（Zero Mean Normalization / Mean-Centering）

公式：

$$x^{\prime }=x-\mu$$

其中：

• $\mu$ 为特征的均值
• $x^{\prime }$ 为归一化后的值

例子：

将房价数据中心对齐到 $0$，便于分析每个房价相对于平均值的偏差。

优点：

• 数据居中后，适合线性代数中的特征处理。
• 提高数据在梯度下降算法中的稳定性。

2.6 标准分数归一化（Z-Score Normalization）

公式：

$$x^{\prime }=\frac{x-\mu }{\sigma }$$

其中：

• $\mu$ 为特征的均值
• $\sigma$ 为特征的标准差
• $x^{\prime }$ 为标准化后的值

例子：

通过标准分数归一化，将房价数据调整为标准正态分布，以消除尺度对模型学习的影响。

优点：

• 标准化后的数据均值为 $0$，方差为 $1$，适合大多数机器学习模型。
• 对异常值较为鲁棒。

2.7 最大绝对值归一化（Max Abs Normalization）

公式：

$$x^{\prime }=\frac{x}{\max (|x|)}$$

其中：

• $x$ 为原始值
• $\max (|x|)$ 为特征的最大绝对值
• $x^{\prime }$ 为归一化后的值

例子：

将房屋面积通过最大绝对值归一化，例如最大房屋面积为 $2000$ 平方英尺，则归一化后最大值为 $1$。

优点：

• 简单高效，适用于稀疏数据。
• 不改变数据的稀疏性，适合非负数据处理。

2.8 总结

归一化适用于以下场景：

1. 未知或非高斯分布：

   • 当数据分布未知或不符合正态分布时（例如，房价分布通常有很高的偏态）。
   • 归一化可以让目标变量误差更均匀分布，提升模型性能。

2. 基于距离的算法：

   • 在使用依赖距离的机器学习算法时（如 k-近邻算法），归一化能防止大尺度特征主导距离计算。

归一化的目标

归一化的核心目标是提高模型性能，例如：

• 正则化目标变量，使误差分布更加平滑；
• 确保输入变量的不同尺度不会互相干扰，避免模型对大值特征的偏倚。

通过正确应用归一化，特征缩放不仅能让模型训练更高效，还能使结果更具解释性。

3 标准化

3.1 介绍

与归一化将特征缩放到特定范围不同，标准化通过将数据调整为均值为 $0$ 和标准差为 $1$ 的形式来实现特征缩放。这一过程涉及减去特征的平均值并除以其标准差。标准化的公式如下：

$$X_{\text{std}}=\frac{X-\mu }{\sigma }$$

其中：

• $X$ 是原始值，
• $\mu$ 是特征的均值，
• $\sigma$ 是特征的标准差。

通过此公式，数据被重新调整，使其分布具有 $0$ 的均值和 $1$ 的标准差。

标准化在以下场景中特别适用：

• 基于梯度的算法：例如支持向量机（SVM）需要标准化的数据以获得最佳性能。虽然线性回归和逻辑回归不强制要求标准化，但当特征尺度差异较大时，标准化能确保每个特征对模型贡献平衡，并帮助优化过程更高效。
• 降维技术：例如主成分分析（PCA）依赖标准化数据来正确识别最大化方差的方向。仅依赖均值归一化可能不足，因为 PCA 考虑了数据的均值和方差，特征的不同尺度会扭曲分析结果。

3.2 代码中的标准化

以下是在 TensorFlow、Keras 和 PyTorch 中实现标准化的代码示例：

TensorFlow 中的标准化代码

import tensorflow as tf

# 数据标准化，标准分数标准化
def z_score_normalization(data):
    mean, variance = tf.nn.moments(data, axes=0)
    std_dev = tf.sqrt(variance)
    normalized_data = (data - mean) / std_dev
    return normalized_data

# 示例数据
data = tf.constant([[1.0, 2.0], [3.0, 4.0], [5.0, 6.0]], dtype=tf.float32)
normalized_data = z_score_normalization(data)
print(normalized_data)

Keras 中的标准化代码

from keras.layers import Normalization
import numpy as np

# 数据标准化层 (标准分数标准化)
data = np.array([[1.0, 2.0], [3.0, 4.0], [5.0, 6.0]])
normalizer = Normalization(axis=-1)  # 按最后一维标准化
normalizer.adapt(data)  # 计算均值和标准差
normalized_data = normalizer(data)
print(normalized_data)

PyTorch 中的标准化代码

import torch
import torch.nn as nn

# 数据标准化 (标准分数标准化)
def z_score_normalization(data):
    mean = data.mean(dim=0, keepdim=True)
    std = data.std(dim=0, keepdim=True)
    normalized_data = (data - mean) / std
    return normalized_data

# 示例数据
data = torch.tensor([[1.0, 2.0], [3.0, 4.0], [5.0, 6.0]])
normalized_data = z_score_normalization(data)
print(normalized_data)

# 使用 PyTorch 的 BatchNorm 层进行标准化
batch_norm = nn.BatchNorm1d(num_features=2)
normalized_data = batch_norm(data)
print(normalized_data)

4 归一化和标准化总结

4.1 对比

尽管归一化和标准化都是特征缩放技术，但它们在方法和应用上有所不同。以下是两者的关键比较：

1. 缩放方法：
   • 归一化：将特征值重新缩放到一个预定义范围内，通常是 $[0,1]$，特别适合特征值范围变化较大的模型。
   • 标准化：将数据中心对齐到均值为 $0$，缩放到标准差为 $1$。
2. 对异常值的敏感性：
   • 不同的归一化技术对异常值的处理能力差异较大。在某些场景下，均值归一化可以成功调整异常值，但其他方法可能不够有效。
   • 一般来说，标准化在处理异常值方面表现更好，因为它明确依赖均值和标准差。
3. 使用场景：
   • 归一化：广泛应用于基于距离的算法（如 k-近邻算法），以确保特征在距离计算中具有相同的权重。
   • 标准化：适用于基于梯度的算法（如 SVM），以及像 PCA 这样的降维技术，其中保持特征方差的正确性非常重要。

归一化和标准化的优点包括提升模型性能和平衡特征贡献。但归一化可能由于固定的比例范围而限制可解释性，而标准化同样可能让解释变得更困难，因为值已不再反映原始单位。也就是说在模型复杂性和准确性之间总是存在权衡。

4.2 可视化

为了理解归一化和标准化之间的差异，使用可视化效果和模型性能对比是非常有帮助的。以下是两个图表展示了不同特征缩放技术的效果：

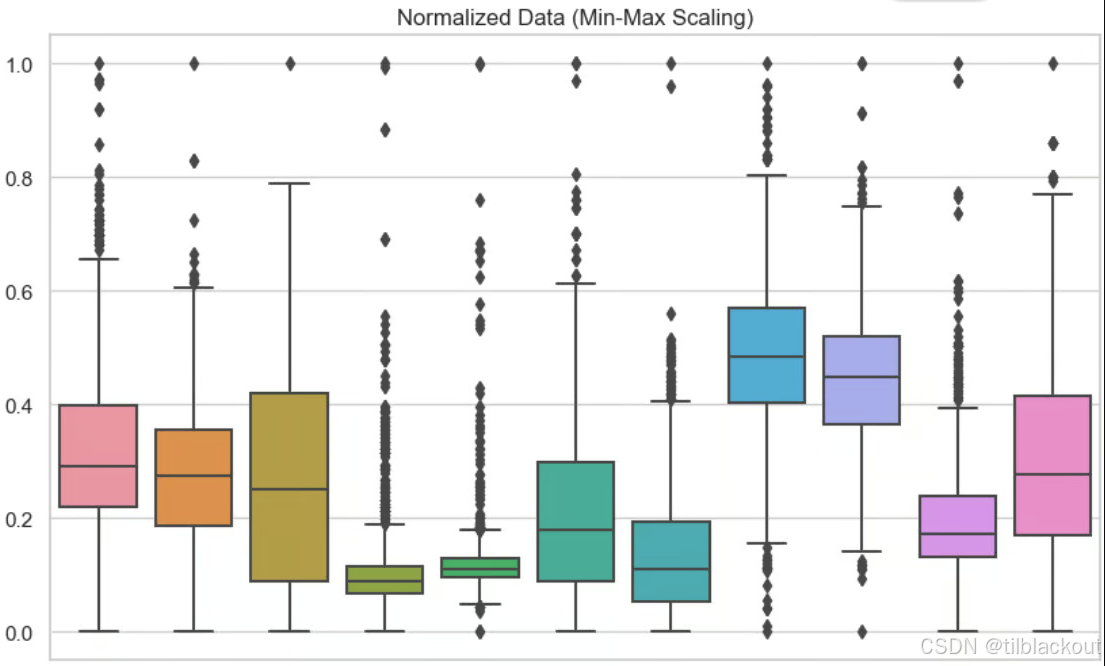
归一化：如下图所示，对数据集中的每个变量使用了最小-最大归一化。从图中可以看出，没有任何值小于 $0$ 或大于 $1$。

• 图片为箱线图，以最左边粉色的箱线为例，我们可以看到：
  • 数据主要集中在 $0.2$ 到 $0.5$ 之间（中间 50% 的范围）。
  • 有一些较大的异常值分布在 $0.8$ 到 $1.0$ 范围。
  • 数据在归一化后保持了其分布特性，但尺度被统一到了 $[0,1]$ 范围，异常值清晰可见。

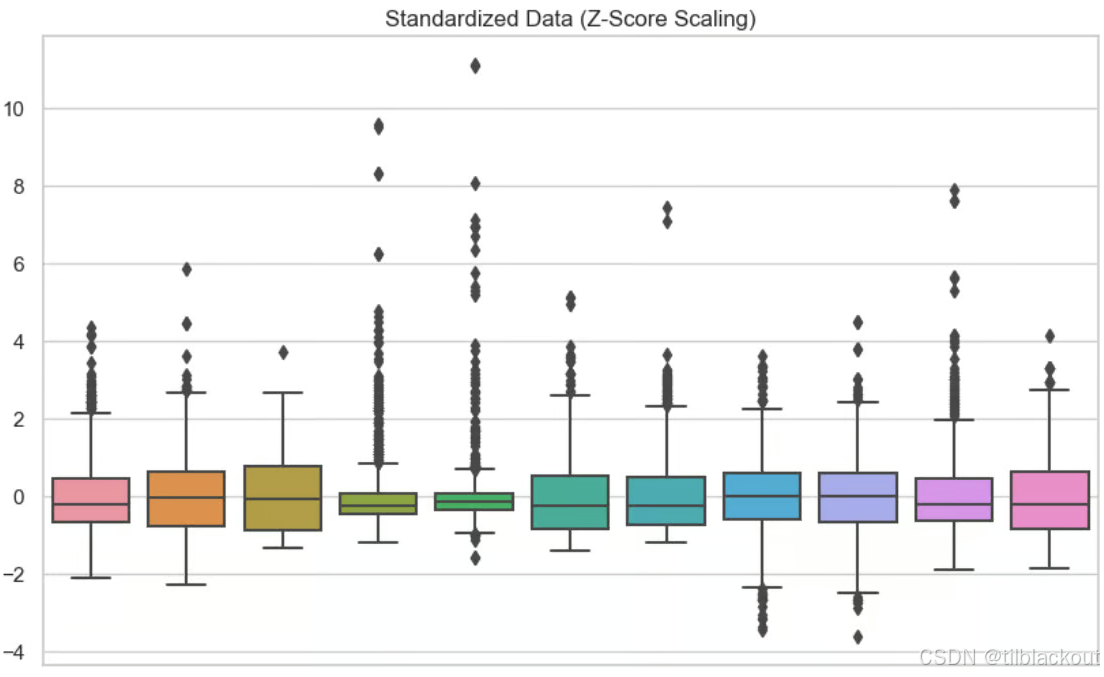
标准化：如下图所示，对每个变量使用了标准化。从图中可以看出，数据以 $0$ 为中心分布。

4.3 线性回归中的归一化与标准化

以下是归一化（均值归一化）和标准化如何改变简单线性回归模型解释的例子：

应用的变换	自变量（房屋面积）	因变量（房价）	解释
均值归一化	均值归一化	原始值	预测的是每单位房屋面积相对于平均值的变化对原始房价的影响。
标准化	标准化	原始值	预测的是每单位房屋面积变化一个标准差对原始房价的影响。
均值归一化	原始值	均值归一化	预测的是原始房屋面积每增加一个单位对房价相对于平均值变化的影响。
标准化	原始值	标准化	预测的是原始房屋面积每增加一个单位对标准化房价的影响。
均值归一化（两者均归一化）	均值归一化	均值归一化	预测的是房屋面积相对于平均值变化对房价相对于平均值变化的影响。
标准化（两者均标准化）	标准化	标准化	预测的是房屋面积每变化一个标准差对房价每变化一个标准差的影响。

在线性回归中，标准化自变量和因变量并不会改变模型的 $R^2$ 值，因为 $R^2$ 度量的是模型对因变量总方差的解释比例，这与数据的尺度无关。然而，标准化会影响误差指标的解释，例如均方根误差（RMSE），因为 RMSE 的单位与因变量一致。当因变量 $y$ 被标准化后，RMSE 将反映误差相对于标准化变量的标准差范围，而不是原始单位的误差，这通常会使 RMSE 值变小。因此，标准化在模型结果解读时需要特别注意其影响，尤其是在比较不同尺度的数据时。

• $R^2$（决定系数，Coefficient of Determination） 是一种统计指标，用于衡量线性回归模型对因变量数据的解释能力，表示模型的拟合优度。

5 总结

特征缩放（包括归一化和标准化）是机器学习中数据预处理的重要组成部分。了解每种技术的适用场景可以显著提升模型的性能和准确性。