本文深入探讨了RNN(循环神经网络)的工作原理，包括其BPTT(反向传播通过时间)过程，以及在处理序列数据时面临的梯度消失和梯度爆炸问题。进一步介绍了LSTM(长短期记忆网络)如何通过特殊的门控机制有效解决这些梯度问题，保持长期依赖性。
RNN(Recurrent Neural Network)由于其递归的网络结构(如图1所示)，对于处理序列建模任务具有独特的优势，因此在许多领域有着广泛的应用。如自然语言处理、语音识别等。
1.RNN的BPTT
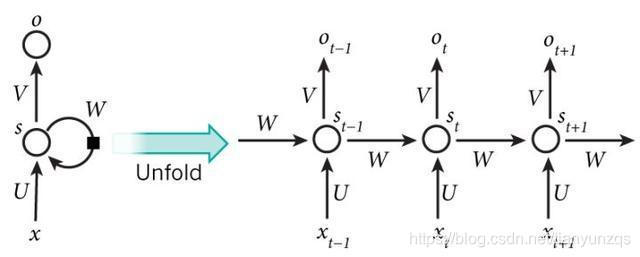
根据RNN的网络结构可写出其基本方程：
S
t
=
δ
(
W
S
t
−
1
+
U
X
t
)
(
1
)
O
t
=
δ
(
V
S
t
)
(
2
)
S_{t} = \delta(WS_{t-1} + UX_{t}) \ \ \ \ \ \ \ (1) \\ O_{t} = \delta(VS_{t}) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (2)
St=δ(WSt−1+UXt) (1)Ot=δ(VSt) (2)
假设交叉熵为其损失函数loss：
L
=
−
∑
t
=
1
n
O
t
l
o
g
O
t
^
(
3
)
L=-\sum_{t=1}^{n}O_{t}log\hat{O_{t}} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (3)
L=−t=1∑nOtlogOt^ (3)
然后分别对W、U、V求偏导
先求V的偏导，因其偏导较为简单
∂
L
∂
V
=
∂
L
∂
O
t
⋅
∂
O
t
∂
V
(
4
)
\frac{\partial L}{\partial V}=\frac{\partial L}{\partial O_{t}}\cdot \frac{\partial O_{t}}{\partial V} \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (4)
∂V∂L=∂Ot∂L⋅∂V∂Ot (4)
再对W和U求偏导
由公式(1)可知，当前时刻的状态不仅与当前的输入有关，而且还与与前一时刻的状态有关。
对W和U运用链式求导
∂
L
∂
W
=
∂
L
∂
O
t
⋅
∂
O
t
∂
S
t
⋅
∂
S
t
∂
S
t
−
1
⋅
∂
S
t
−
1
∂
S
t
−
2
⋅
.
.
.
⋅
⋅
∂
S
1
∂
S
0
⋅
∂
S
0
∂
W
=
∂
L
∂
O
t
⋅
∂
O
t
∂
S
t
⋅
∏
k
=
1
t
∂
S
k
∂
S
k
−
1
⋅
∂
S
k
−
1
∂
W
(
5
)
\begin{aligned} \frac{\partial L}{\partial W}&=\frac{\partial L}{\partial O_{t}}\cdot \frac{\partial O_{t}}{\partial S_{t}}\cdot \frac{\partial S_{t}}{\partial S_{t-1}}\cdot \frac{\partial S_{t-1}}{\partial S_{t-2}}\cdot...\cdot \cdot \frac{\partial S_{1}}{\partial S_{0}}\cdot \frac{\partial S_{0}}{\partial W}\\ &=\frac{\partial L}{\partial O_{t}}\cdot \frac{\partial O_{t}}{\partial S_{t}}\cdot \prod_{k=1}^{t} \frac{\partial S_{k}}{\partial S_{k-1}}\cdot \frac{\partial S_{k-1}}{\partial W}\ \ \ \ \ (5) \end{aligned}
∂W∂L=∂Ot∂L⋅∂St∂Ot⋅∂St−1∂St⋅∂St−2∂St−1⋅...⋅⋅∂S0∂S1⋅∂W∂S0=∂Ot∂L⋅∂St∂Ot⋅k=1∏t∂Sk−1∂Sk⋅∂W∂Sk−1 (5)
同理可得
∂
L
∂
U
=
∂
L
∂
O
t
⋅
∂
O
t
∂
S
t
⋅
∂
S
t
∂
S
t
−
1
⋅
∂
S
t
−
1
∂
S
t
−
2
⋅
.
.
.
⋅
⋅
∂
S
1
∂
S
0
⋅
∂
S
0
∂
U
=
∂
L
∂
O
t
⋅
∂
O
t
∂
S
t
⋅
∏
k
=
1
t
∂
S
k
∂
S
k
−
1
⋅
∂
S
k
−
1
∂
U
(
6
)
\begin{aligned} \frac{\partial L}{\partial U}&=\frac{\partial L}{\partial O_{t}}\cdot \frac{\partial O_{t}}{\partial S_{t}}\cdot \frac{\partial S_{t}}{\partial S_{t-1}}\cdot \frac{\partial S_{t-1}}{\partial S_{t-2}}\cdot...\cdot \cdot \frac{\partial S_{1}}{\partial S_{0}}\cdot \frac{\partial S_{0}}{\partial U}\\ &=\frac{\partial L}{\partial O_{t}}\cdot \frac{\partial O_{t}}{\partial S_{t}}\cdot \prod_{k=1}^{t} \frac{\partial S_{k}}{\partial S_{k-1}}\cdot \frac{\partial S_{k-1}}{\partial U}\ \ \ \ \ (6) \end{aligned}
∂U∂L=∂Ot∂L⋅∂St∂Ot⋅∂St−1∂St⋅∂St−2∂St−1⋅...⋅⋅∂S0∂S1⋅∂U∂S0=∂Ot∂L⋅∂St∂Ot⋅k=1∏t∂Sk−1∂Sk⋅∂U∂Sk−1 (6)
2.RNN梯度消失与梯度爆炸
由公式(1)可知
∂
S
t
∂
S
t
−
1
=
W
⋅
σ
′
(
7
)
\frac{\partial S_{t}}{\partial S_{t-1}}=W\cdot {\sigma }'\ \ \ \ \ (7)
∂St−1∂St=W⋅σ′ (7)
sigmod函数
当公式(7)的乘积小于1时，公式(5)和公式(6)就会趋近于0，也即梯度消失；
当公式(7)的乘积大于1时，公式(5)和公式(6)就会趋近于无穷大，也即梯度爆炸；
3.LSTM解决RNN梯度问题
PS：图片来源于http://colah.github.io/posts/2015-08-Understanding-LSTMs/ 下面公式中的标号参考该链接中图片标号。
i
t
=
σ
(
W
i
[
h
t
−
1
;
x
t
]
+
b
i
)
(
8
)
f
t
=
σ
(
W
f
[
h
t
−
1
;
x
t
]
+
b
f
)
(
9
)
C
~
t
=
t
a
n
h
(
W
c
[
h
t
−
1
;
x
t
]
+
b
c
)
(
10
)
C
t
=
i
t
∗
C
~
t
+
f
t
∗
C
t
−
1
(
11
)
o
t
=
σ
(
W
o
[
h
t
−
1
;
x
t
]
+
b
o
)
(
12
)
h
t
=
o
t
∗
t
a
n
h
(
C
t
)
(
13
)
\begin{aligned} i_{t}&=\sigma (W_{i}[h_{t-1}; x_{t}]+b_{i}) \ \ \ \ \ \ \ (8) \\ f_{t}&=\sigma (W_{f}[h_{t-1}; x_{t}]+b_{f}) \ \ \ \ \ \ (9) \\ \tilde{C}_{t}&=tanh (W_{c}[h_{t-1}; x_{t}]+b_{c}) \ \ (10) \\ C_{t}&=i_{t}*\tilde{C}_{t}+f_{t}*C_{t-1} \ \ \ \ \ \ \ \ (11) \\ o_{t}&=\sigma (W_{o}[h_{t-1}; x_{t}]+b_{o}) \ \ \ \ \ \ (12) \\ h_{t}&=o_{t}*tanh(C_{t}) \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ (13) \\ \end{aligned}
itftC~tCtotht=σ(Wi[ht−1;xt]+bi) (8)=σ(Wf[ht−1;xt]+bf) (9)=tanh(Wc[ht−1;xt]+bc) (10)=it∗C~t+ft∗Ct−1 (11)=σ(Wo[ht−1;xt]+bo) (12)=ot∗tanh(Ct) (13)
类比RNN中偏导的连乘部分，LSTM中连乘部分为
∂
C
t
∂
C
t
−
1
=
f
t
=
σ
(
14
)
\frac{\partial C_{t}}{\partial C_{t-1}}=f_{t}=\sigma \ \ \ \ \ \ \ \ \ (14)
∂Ct−1∂Ct=ft=σ (14)
对比公式(7)和公式(14)，LSTM的连乘部分变成了σ，在实际参数更新过程中，通过控制其值接近于1，则经过多次连乘(训练)后，梯度也不会消失；而σ的值不会大于1，故不会出现梯度爆炸。
扫一扫
1万+
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
