Codeforces Contest 1075 problem E Optimal Polygon Perimeter —— 找凸包中曼哈顿距离之和最大的多边形

You are given n points on the plane. The polygon formed from all the n points is strictly convex, that is, the polygon is convex, and there are no three collinear points (i.e. lying in the same straight line). The points are numbered from 1 to n, in clockwise order.

We define the distance between two points p1=(x1,y1) and p2=(x2,y2) as their Manhattan distance:
d(p1,p2)=|x1−x2|+|y1−y2|.
Furthermore, we define the perimeter of a polygon, as the sum of Manhattan distances between all adjacent pairs of points on it; if the points on the polygon are ordered as p1,p2,…,pk (k≥3), then the perimeter of the polygon is d(p1,p2)+d(p2,p3)+…+d(pk,p1).

For some parameter k, let’s consider all the polygons that can be formed from the given set of points, having any k vertices, such that the polygon is not self-intersecting. For each such polygon, let’s consider its perimeter. Over all such perimeters, we define f(k) to be the maximal perimeter.

Please note, when checking whether a polygon is self-intersecting, that the edges of a polygon are still drawn as straight lines. For instance, in the following pictures:

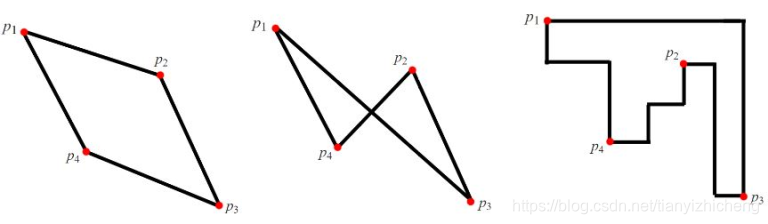
In the middle polygon, the order of points (p1,p3,p2,p4) is not valid, since it is a self-intersecting polygon. The right polygon (whose edges resemble the Manhattan distance) has the same order and is not self-intersecting, but we consider edges as straight lines. The correct way to draw this polygon is (p1,p2,p3,p4), which is the left polygon.

Your task is to compute f(3),f(4),…,f(n). In other words, find the maximum possible perimeter for each possible number of points (i.e. 3 to n).

Input
The first line contains a single integer n (3≤n≤3⋅105) — the number of points.

Each of the next n lines contains two integers xi and yi (−108≤xi,yi≤108) — the coordinates of point pi.

The set of points is guaranteed to be convex, all points are distinct, the points are ordered in clockwise order, and there will be no three collinear points.

Output
For each i (3≤i≤n), output f(i).

Examples
inputCopy
4
2 4
4 3
3 0
1 3
outputCopy
12 14
inputCopy
3
0 0
0 2
2 0
outputCopy
8
Note
In the first example, for f(3), we consider four possible polygons:

(p1,p2,p3), with perimeter 12.
(p1,p2,p4), with perimeter 8.
(p1,p3,p4), with perimeter 12.
(p2,p3,p4), with perimeter 12.
For f(4), there is only one option, taking all the given points. Its perimeter 14.

In the second example, there is only one possible polygon. Its perimeter is 8.

题意：

顺时针给你n个点，保证这是个凸包，设定距离为两个点的哈夫曼距离，让你求出从3到n边型所有点的哈夫曼距离的和最大。

题解：

这里有一个比较重要的概念，就是，党确定了上下左右四个界限的时候，边数大于等于4的图形它的距离之和就是这些界限上的那个点的和，举个例子：
比如说这是4边形最大和的图：

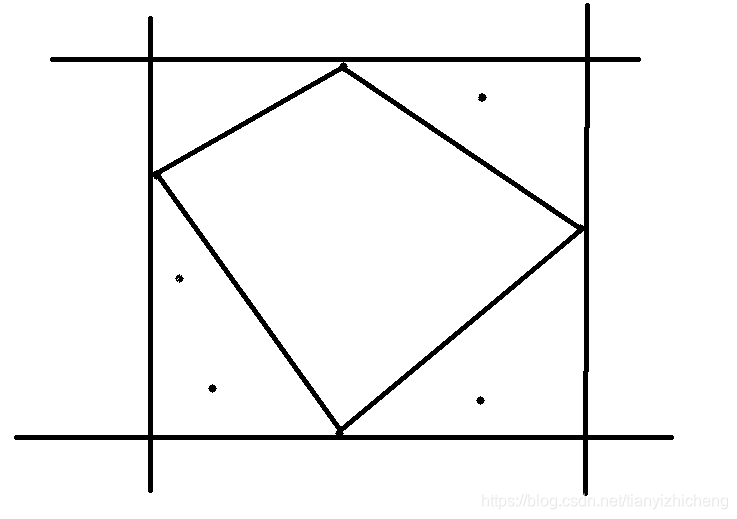
那么就算之后再加边，这些黑色部分的和也是红色部分，就是一样的：

但是三角形的话就需要考虑四种情况：
最大的x+最大的y作为两个顶点，
最大的x+最小的y
最小的x+最大的y
最小的x+最小的y
那么这道题就解决了

#include<bits/stdc++.h>
using namespace std;
const int N=3e5+5;
int x[N],y[N];
int main()
{
    int n;
    scanf("%d",&n);
    int maxx,maxy,minx,miny;
    int ans;
    for(int i=1;i<=n;i++)
    {
        scanf("%d%d",&x[i],&y[i]);
        if(i==1)
            maxx=minx=x[i],maxy=miny=y[i];
        else
            maxx=max(maxx,x[i]),minx=min(minx,x[i]),maxy=max(maxy,y[i]),miny=min(miny,y[i]);
    }
    if(n==3)
        printf("%d\n",2*(maxx-minx)+2*(maxy-miny));
    else
    {
        ans=0;
        for(int i=1;i<=n;i++)
        {
            ans=max(ans,2*(maxx-x[i]+maxy-y[i]));
            ans=max(ans,2*(x[i]-minx+maxy-y[i]));
            ans=max(ans,2*(maxx-x[i]+y[i]-miny));
            ans=max(ans,2*(x[i]-minx+y[i]-miny));
        }
        printf("%d ",ans);
        for(int i=4;i<=n;i++)
            printf("%d%c",2*(maxx-minx+maxy-miny),i==n?'\n':' ');
    }
    return 0;
}