Mayor's posters —— 线段树区间更新

The citizens of Bytetown, AB, could not stand that the candidates in the mayoral election campaign have been placing their electoral posters at all places at their whim. The city council has finally decided to build an electoral wall for placing the posters and introduce the following rules:
Every candidate can place exactly one poster on the wall.
All posters are of the same height equal to the height of the wall; the width of a poster can be any integer number of bytes (byte is the unit of length in Bytetown).
The wall is divided into segments and the width of each segment is one byte.
Each poster must completely cover a contiguous number of wall segments.

They have built a wall 10000000 bytes long (such that there is enough place for all candidates). When the electoral campaign was restarted, the candidates were placing their posters on the wall and their posters differed widely in width. Moreover, the candidates started placing their posters on wall segments already occupied by other posters. Everyone in Bytetown was curious whose posters will be visible (entirely or in part) on the last day before elections.
Your task is to find the number of visible posters when all the posters are placed given the information about posters’ size, their place and order of placement on the electoral wall.
Input
The first line of input contains a number c giving the number of cases that follow. The first line of data for a single case contains number 1 <= n <= 10000. The subsequent n lines describe the posters in the order in which they were placed. The i-th line among the n lines contains two integer numbers l i and ri which are the number of the wall segment occupied by the left end and the right end of the i-th poster, respectively. We know that for each 1 <= i <= n, 1 <= l i <= ri <= 10000000. After the i-th poster is placed, it entirely covers all wall segments numbered l i, l i+1 ,… , ri.
Output
For each input data set print the number of visible posters after all the posters are placed.

The picture below illustrates the case of the sample input.

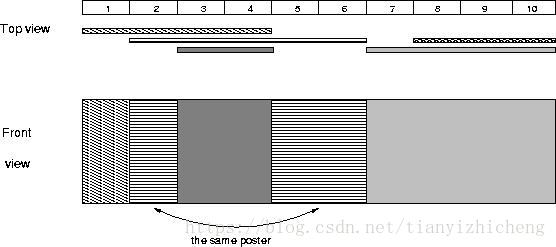
Sample Input
1
5
1 4
2 6
8 10
3 4
7 10
Sample Output
4

题意：

按次序给你n个位置为到r的海报，这些海报贴在一张墙上，意味着他们能被后来贴的覆盖
问你最终能看到几张海报。

题解：

线段树区间更新，先离散化。

#include<iostream>
#include<stdio.h>
#include<string.h>
#include<algorithm>
using namespace std;
const int maxn=40005;
int num[maxn*4],flag[maxn*4];
void pushdown(int root)
{
    if(!flag[root])
        return ;
    num[root<<1]=flag[root];
    num[root<<1|1]=flag[root];
    flag[root<<1]=flag[root];
    flag[root<<1|1]=flag[root];
    flag[root]=0;
}
void update(int l,int r,int root,int ql,int qr,int val)
{
    if(l>=ql&&r<=qr)
    {
        num[root]=flag[root]=val;
        return ;
    }
    pushdown(root);
    int mid=l+r>>1;
    if(mid>=ql)
        update(l,mid,root<<1,ql,qr,val);
    if(mid<qr)
        update(mid+1,r,root<<1|1,ql,qr,val);
}
int vis[20005];
int query(int l,int r,int root)
{

    if(l==r)
    {
        if(num[root]&&!vis[num[root]])
        {
            vis[num[root]]=1;
            return 1;
        }
        return 0;
    }
    pushdown(root);
    int mid=l+r>>1;
    int ans=0;
    ans+=query(l,mid,root<<1);
    ans+=query(mid+1,r,root<<1|1);
    return ans;
}
struct node
{
    int l,r;
}nod[10005];
int a[20005];
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        memset(num,0,sizeof(num));
        memset(flag,0,sizeof(flag));
        memset(vis,0,sizeof(vis));
        int n;
        scanf("%d",&n);
        int l,r;
        for(int i=1;i<=n;i++)
            scanf("%d%d",&nod[i].l,&nod[i].r),a[i*2-1]=nod[i].l,a[i*2]=nod[i].r;
        sort(a+1,a+1+2*n);
        int all=unique(a+1,a+1+2*n)-a-1;
        for(int i=1;i<=n;i++)
            update(1,20000,1,lower_bound(a+1,a+1+all,nod[i].l)-a,lower_bound(a+1,a+1+all,nod[i].r)-a,i);
        printf("%d\n",query(1,20000,1));
    }
    return 0;
}