C++中的AVL树-优快云博客

本文链接：https://blog.youkuaiyun.com/tianxhiliangtadi/article/details/144543344

一、AVL树存在的意义

二叉搜索树有时会退化为单支树，此时进行查找效率相当于顺序表，十分低下，为此提出平衡二叉搜索树的概念：当向二叉搜索树中插入新节点时，使左右子树的高度差不超过1

1.补：为什么不让高度差相等？

只有当节点数是(2^n)-1的时候，也就是满二叉树的时候才能左右完全相等，因此不超过1是相对最好的情况

二、一个标准的AVL树

①左右子树都是AVL树

②左右子树的高度差（又称平衡因子），绝对值不超过1（即-1/0/1），一般选择用右子树高度减左子树高度来计算平衡因子

对于一个AVL树的节点：

struct AVLTreeNode
{
	pair<K, V> _kv;
	AVLTreeNode<K, V>* _left;
	AVLTreeNode<K, V>* _right;
	AVLTreeNode<K, V>* _parent;//因为AVL树要进行旋转来调整树的高度，期间需要访问节点的父节点

	int _bf;//平衡因子
};

一棵AVL树的图示、

三、AVL树的插入

按照搜索二叉树的逻辑插入，插入之后连接上父节点，接下来需要更新平衡因子，分两种情况：

①插入在左子树，parent平衡因子--

②插入在右子树，parent平衡因子++

更新之后要考虑是否需要继续更新，这是由parent更新之后的平衡因子决定的，可以分为三种情况

①parent的平衡因子==0

这说明更新之前parent平衡因子是1/-1，插入节点插入在了矮的一边，parent所在子树高度不变，不需要向上更新了

②parent的平衡因子==1/-1

这说明更新之前parent平衡因子是0，插入节点插入在了任意一边，parent所在子树高度改变，需要向上继续更新

③parent的平衡因子==2/-2

这说明更新之前parent平衡因子是1/-1，插入节点插入在了高的一边，parent所在子树高度改变并且树的平衡被破坏，需要进行旋转处理

④parent的平衡因子不是这五个数

可以通过assert来停止执行程序，这说明之前的更新逻辑出现问题了，需要检查修改

⭐⭐⭐⭐⭐

当进行完旋转逻辑后，我们就不需要再向上更新了，此时务必break一下，否则会出现未知的错误

四、AVL树插入时的旋转

AVL树在插入时的旋转可以分为四种，

4.1左单旋

4.1.1旋转逻辑展示

旋转的原则是①保持搜索树的规则不变

②控制平衡，降低高度

就此，我们可以画出旋转的抽象图

旋转前：旋转后：

不难发现，30作为根节点，起初其平衡因子是2；60作为根节点右孩子，起初平衡因子是1

观察图可以发现，我们着重要处理3点：

①subRL变为parent的右边

②parent变为subR的左边

③subR变成这棵子树的根

4.1.2实例的情况：

在由抽象图对应实例的时候，

当h==0，只有两个节点和一个新插入节点，可能的情况为一种

当h==1，因为a，b，c都只有一种可能，所以对应可能的情况为一种

当h==2，因为a，b，c中，a有三种可能的情况，b有三种可能的情况，c有一种可能的情况（c只能是高度为2的满二叉树，单只树的话平衡因子一定会在更新到parent之前就出现不平衡的状况），在插入结点的时候有四种可能的情况

算下来3*3*1*4=36种可能的情况

当h>=3之后，情况的数量会出现爆炸式增长

4.1.3实现

完成上述分析后，我们就可以按照这样的思路进行旋转逻辑的实现了

①完成观察图所得出的三个节点位置改变

②完成对各节点parent关系的处理

③检验这是一整棵树还是一棵子树，进行调整后根节点subR的更新

④更新平衡因子

4.1.4代码参考

void RotateL(Node* parent)
{
	//先直接改，然后考虑每个更改后的父节点问题，最后修改平衡因子
	Node* subR = parent->_right;
	Node* subRL = subR->_left;

	parent->_right = subRL;
	subR->_left = parent;

	//然后修改父节点问题
	Node* parentParent = parent->_parent;

	//对应h=0的情况
	if (subRL != nullptr)
	{
		subRL->_parent = parent;
	}

	subR->_parent = parentParent;
	parent->_parent = subR;
	if (parentParent != nullptr)
	{

		if (parentParent->_left == parent)
		{
			parentParent->_left = subR;
		}
		else
		{
			parentParent->_right = subR;
		}

	}
	else
		_root = subR;

	//最后修改平衡因子
	subR->_bf = 0;
	parent->_bf = 0;

}

4.1补：

抽象例子种以30为根这棵树有可能是一整棵树，也有可能是一棵树的子树，其中60这一节点本质上是平衡因子为2的节点的右孩子节点

4.2右单旋

4.2.1旋转逻辑演示

旋转前：旋转后：

不难发现，60作为根节点，起初其平衡因子是-2；30作为根节点左孩子，起初平衡因子是-1

观察图可以发现，我们着重要处理3点：

①subLR变为parent的左边

②parent变为subL的右边

③subL变成这棵子树的根

实现过程与左单旋同理

4.2.2代码参考

//右旋逻辑
void RotateR(Node* parent)
{
	Node* subL = parent->_left;
	Node* subLR = subL->_right;

	parent->_left = subLR;
	subL->_right = parent;

	//处理父节点问题
	if (subLR)
	{
		subLR->_parent = parent;
	}
	Node* parentParent = parent->_parent;
	subL->_parent = parentParent;
	parent->_parent = subL;

	if (parentParent)
	{
		if (parent == parentParent->_left)
		{
			parentParent->_left = subL;
		}
		else
		{
			parentParent->_right = subL;
		}
	}
	else
		_root = subL;

	subL->_bf = parent->_bf = 0;
}

4.3右左双旋

4.3.1需求的变化

左单旋处理的是：而现在要处理：

在这里会发现，30作为根节点，起初其平衡因子是2；60作为根节点右孩子，起初平衡因子不再是1，而变成了-1

为了将其变得平衡，我们的解决办法是先以60为parent右旋，再以30为parent左旋

4.3.2抽象情况变化

因为要以60为parent进行一次右旋，因此对于原来b部分需要进行拆分处理，

需要添加新的例子节点50，为原来b部分子树的根节点

在插入的时候（若h>0）左右孩子会影响50的平衡因子，而50的平衡因子对于最后旋转完成后平衡因子的更新有影响

①我们先假设在分割后的b部分下插入节点

此时待处理的是

经过一次右单旋

进行了这次右旋之后，树的结构变成了左单旋处理的结构，接下来只需按照左单旋的思路进行旋转即可

完成旋转后，可以发现subRL，subR，parent的平衡因子分别变成了0，1，0

②如果在分割后的c部分下插入节点

待处理的情况：处理最终情况：

完成旋转后，可以发现subRL，subR，parent的平衡因子分别变成了0，0，-1

③如果h==0，平衡因子与前两种情况都不同

此时待处理的情况是：处理的结果是：

完成旋转后，可以发现subRL，subR，parent的平衡因子分别变成了0，0，0

4.3.3关于h范围对情况的影响

①当h==0时，是一种单独的情况，会把subRL，subR，parent的平衡因子都置为0

②当h==1时，插入位置在50的左右都可以，有两种情况，插入位置在左和右的平衡因子会出现不同情况

③当h>=2时，插入位置会变得非常多，总情况数爆炸式增长

4.3.4代码参考

void RotateRL(Node* parent)
{
	Node* subR = parent->_right;
	Node* subRL = subR->_left;

	int tmp = subRL->_bf;

	RotateR(subR);
	RotateL(parent);

	//接下来要更新平衡因子
	if (tmp == 0)
	{
		subR->_bf = 0;
		subRL->_bf = 0;
		parent->_bf = 0;
	}
	else if (tmp == -1)
	{
		subR->_bf = 1;
		subRL->_bf = 0;
		parent->_bf = 0;
	}
	else if (tmp == 1)
	{
		subR->_bf = 0;
		subRL->_bf = 0;
		parent->_bf = -1;
	}
	else
		assert(false);//当走到这一步的时候一定是出问题了，因为平衡因子不该出现-1，0，1之外的值
}

4.4左右双旋

4.4.1需求改变

右单旋处理的是：而现在的情况是：

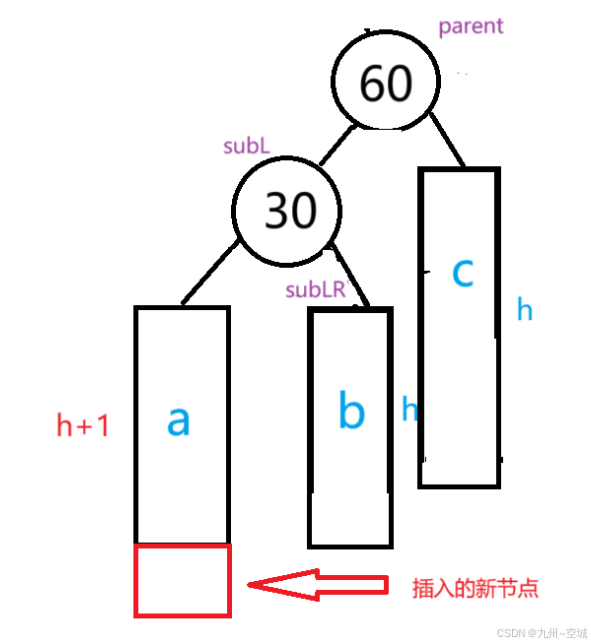
在这里会发现，60作为根节点，起初其平衡因子是-2；30作为根节点左孩子，起初平衡因子不再是-1，而变成了1

为了将其变得平衡，我们的解决办法是先以30为parent左旋，再以60为parent右旋

4.4.2抽象情况变化

以30为parent左旋，需要用到30的右孩子节点，我们设为50

①假设在分割后的c部分下插入节点

待处理的情况:

一次以30为parent的左单旋

再经过一次以60为parent的右单旋

完成旋转后，可以发现subLR，subL，parent的平衡因子分别变成了0，-1，0

②假设在分割后的b部分下插入节点

待处理：处理后：

完成旋转后，可以发现subLR，subL，parent的平衡因子分别变成了0，0，1

③如果h==0，平衡因子与前两种情况都不同

此时待处理的情况是：处理后：

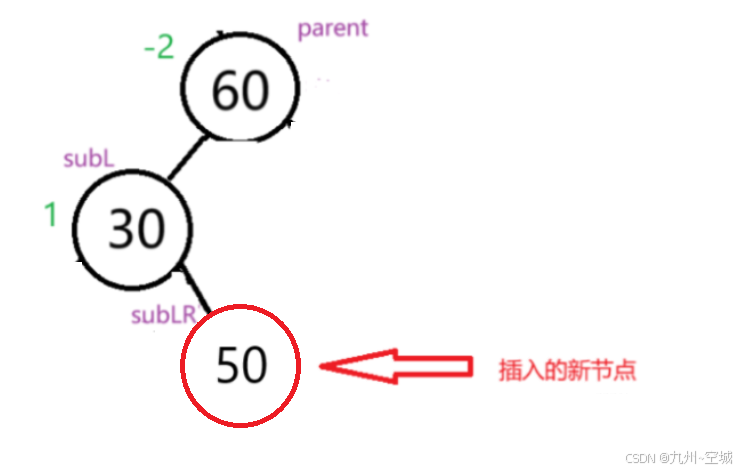
完成旋转后，可以发现subLR，subL，parent的平衡因子分别变成了0，0，0

4.4.3代码参考

void RotateLR(Node* parent)
{
	Node* subL = parent->_left;
	Node* subLR = subL->_right;

	int tmp = subLR->_bf;

	RotateL(subL);
	RotateR(parent);

	if (tmp == 0)
	{
		parent->_bf = 0;
		subL->_bf = 0;
		subLR->_bf = 0;

	}
	else if (tmp == 1)
	{
		parent->_bf = 0;
		subL->_bf = -1;
		subLR->_bf = 0;
	}
	else if (tmp == -1)
	{
		parent->_bf = 1;
		subL->_bf = 0;
		subLR->_bf = 0;
	}
	else
		assert(false);

}