原创 | 投影坐标系6位和8位的区别（GIS）

#GIS#，#ArcGIS#，#地理信息系统#

关于坐标的问题真的可以写十几篇技术文章哎~

今天我们只聊投影坐标系中常说的6位坐标和8位坐标的区别。

 

01 分清XY

地理坐标系下我们使用经度和纬度来表示，大家都能分清经度表示东西向的，纬度表示南北向的。

来源：百度

那么投影坐标系下呢？在测绘里，XY的方向和我们熟知的数学坐标系中的坐标轴是相反的。

来源：百度

所以这里的6位和8位指的是测量坐标系中的Y值。

其实不同的坐标系，Y值可能是6位、7位、8位，那为什么只听说6位和8位的区别呢？

因为通常我们讨论的特指我国常用投影方式——高斯克吕格投影，以中央经线命名和以带号命名导致的Y值是6位和8位的问题。

02 高斯克吕格投影

高斯克吕格投影是分带投影，有3°带分带法（中央经线两侧各1.5°）和6°带分带法（中央经线两侧各3°），将全球分为如图这种橘子瓣形状：

图片莫名其妙上传失败，建议去公众号GIS小助手原文看吧。。。

它的命名方式有两种：

①不带带号：假东偏500km.

3°分带法不带带号

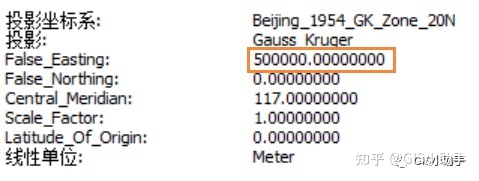
6°分带法不带带号

②带带号：假东偏=带号+500km

3°分带法带带号

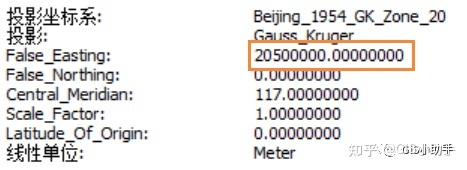
6°分带法带带号

地球赤道周长40075千米，共360°，则3°长为334千米，则6°分带法每个橘子瓣中Y坐标范围为(-334 000m)~334 000m，区间差为668千米；3°分带法每个橘子瓣中Y坐标范围为(-167 000m)~167 000m，区间差为334千米。

为避免坐标出现负数、不便于记录和计算，需要将X轴向西移动，Y轴向南移动，从而保证所有数据都在第一象限。移动的距离就是假东偏、假北偏的距离。

高斯克吕格投影3°和6°的移动距离都是500 000m，这也就是假东偏的距离，表示Y坐标需要统一加500 000m，所以6°带坐标范围为166 000m~834 000m，3°带坐标范围为333 000m~667 000m，结果为六位数。

同样的，以带号命名的，假东偏的距离是带号+500千米：6°带以20带为例，假东偏为20 500 000，坐标范围为20 166 000m~20 834 000m；3°带以40带为例，假东偏为40 500 000，坐标范围为40 333 000m~40 667 000m，结果为八位数，前两位表示带号。

03 根据位数判定坐标

不同的命名方式会导致坐标的范围不一样，反过来，如果已经知道坐标的范围能不能倒推坐标系呢？

可以，但是得分情况。这里我们只讨论高斯克吕格投影。

假设已经知道数据的投影是高斯克吕格，怎样判定是6°带还是3°带？怎样判定中央经线是多少呢？

如果坐标范围是6位，我们可以判定坐标系不带带号的。如果Y值范围在333 000m~667 000m，可能是3°分带法；如果Y值范围在166 000m~834 000m，一定是6°分带法。

比如下图：从左右范围可以看到这份数据的Y值是六位，范围是430 669m~604 511m，所以这一定是不带带号的坐标命名方式，大概率是3°分带法。

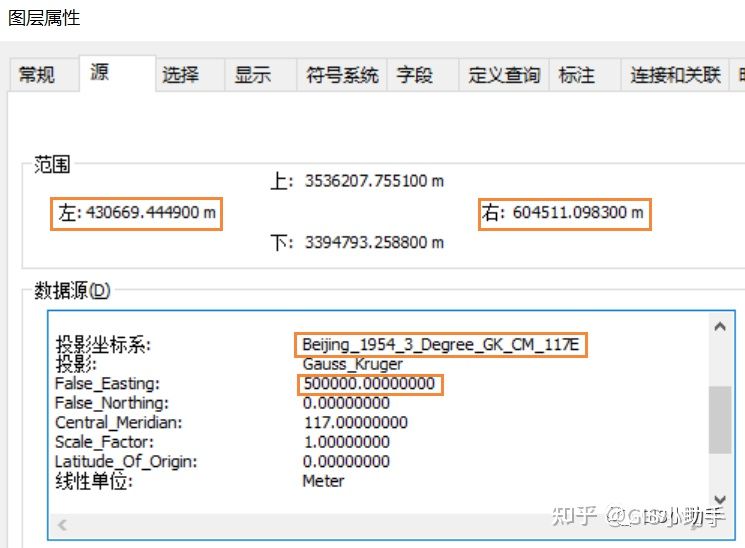
这里为什么不能肯定是3°分带法，看下图：同一份数据在6°分带法下的范围也是430 669m~604 511m。

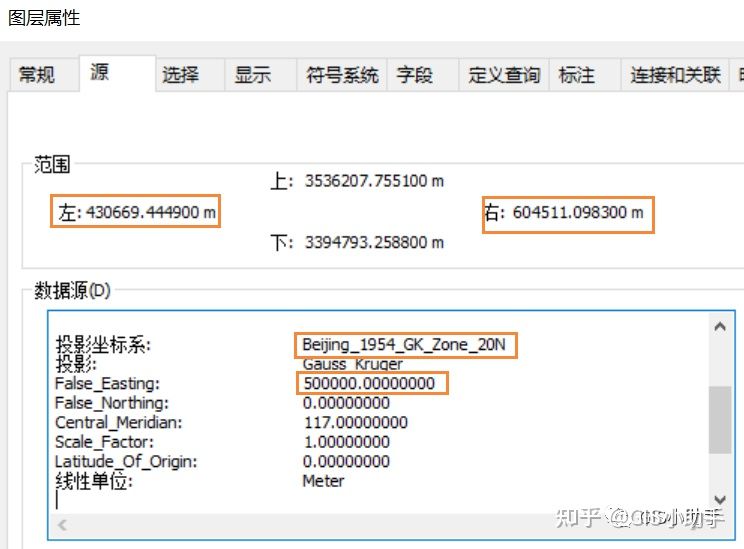
因此如果坐标范围是6位，可获取的信息非常有限。

如果坐标范围是8位，我们可以判定坐标系是以带号命名，并且根据带号可以知道是3°带还是6°带。

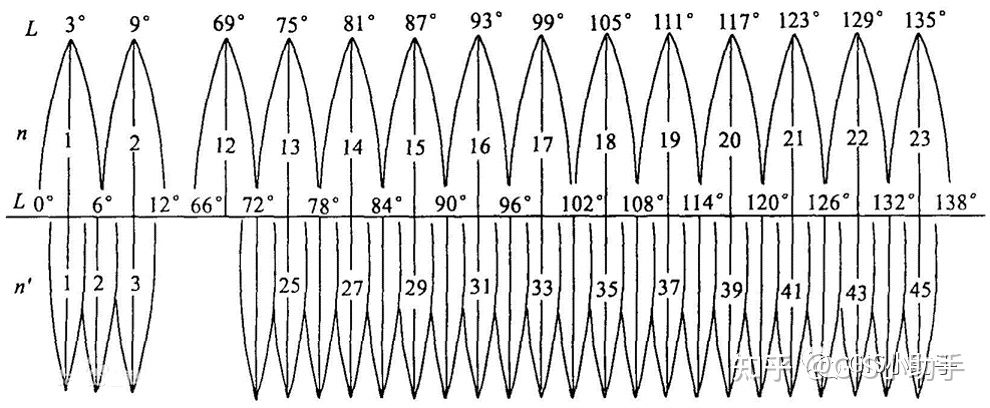
仔细观察分带投影，因为我们国家的经度范围大致在73°33′E~105°05′E，所以如果是以带号命名，带号在13~23带之间的，说明是6°分带法；带号在25~45带之间的，说明是3°分带法。

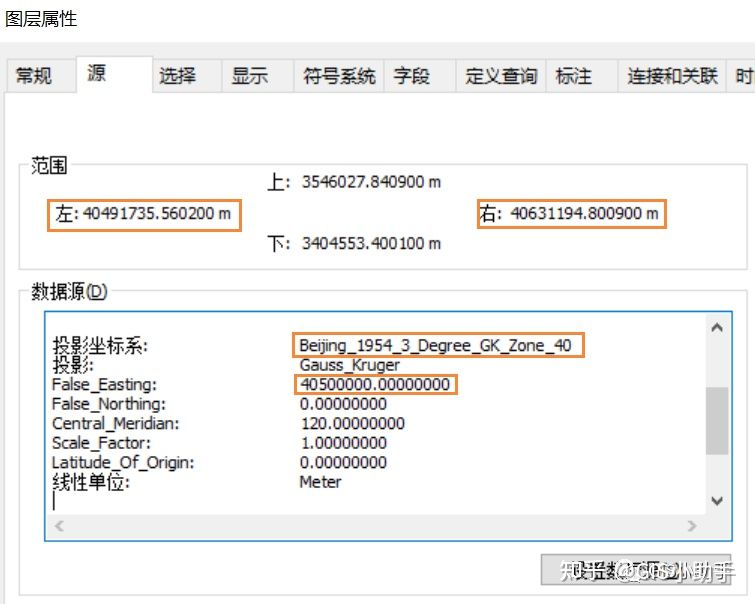
比如下图：从左右范围可以看到这份数据的Y值是八位，前两位是40，所以这一定是3°带以带号命名的坐标系，中央经线是120°E。

——END——

写在最后：

这次的方法其实是帮助你判定坐标的，如果数据已经有坐标了，这篇文章的内容你全都可以跳过！想搞懂坐标真的好难！本篇文章是我的心血之作，未经允许不可转载，但欢迎转发到朋友圈~

谢谢你们关注我的公众号！爱你们~

扫我扫我（公众号：GIS小助手）