电动汽车IMT系统振荡阻尼控制

第7章 传动系统设计和电动汽车控制

7.1 引言

地面车辆的替代动力总成方案随着电动化车辆（包括混合动力汽车 （HEV）和纯电动汽车（PEV））的重新兴起而吸引了越来越多的 研究关注（吴等，2015）。HEV能够利用汽油与电能之间的能量管 理优势，而PEV只能依靠电能驱动（马朱布等，2013）。HEV的动 力总成结构通常可分为串联、并联和功率分流式混合。而对于 PEV，则可简单划分为分布式电机驱动和集中式电机驱动（罗和谭， 2013）。分布式电机驱动PEV（例如四轮独立驱动电动汽车）的动 力总成结构与传统车辆大不相同。在分布式电机驱动PEV中，机械 传动系统和差速器不再必要，车辆由轮毂电机直接驱动（霍里， 2004；王等，2011）。这种执行灵活性已在状态估计、能量优化和 容错控制等方面吸引了大量针对分布式电机驱动电动汽车的研究工 作（黄和王，2013；陈和王，2012；王和王，2012）。对于集中式 电机驱动PEV，传统车辆动力总成系统中的某些装置仍可保留，仅 将内燃机（ICE）替换为电机。尽管分布式电机驱动PEV更具创新 性和灵活性，但由于其与传统车辆相似，集中式电机驱动PEV目前 仍是主流（萨瓦吉安等，2011）。相比内燃机，电动机通常具有更 高的效率、更好的启动性能以及更平坦的效率图谱。因此，大多数 现代PEV普遍采用具有固定传动比的单速驱动系统以简化传动系统 结构

245
电动车辆的建模、动力学与控制DOI: htt p ://dx.doi.or g /10.1016/B978-0-12-812786-5.00007-0
版权所有©2018爱思唯尔公 司。保留所有权利。
本文档由funstory.ai的开源PDF翻译库BabelDOCv0.5.10(http://yadt.io)翻译，本仓库正在积极的建设当中，欢迎star和关注。

（霍夫曼和戴，2010）。然而，采用多速变速器——包括自动机械 变速器（AMT）（奚等，2008；索尔诺蒂等，2012；余和曾， 2013；赵等，2014a,b,c；高等，2015；陈等，2016）、两速双离 合变速器（DCT）（周等，2014；朱等，2014；洪等，2015；阮 等，2016）以及专用行星齿轮组（PGS）（穆萨维等，2015；方等， 2016）——可以为PEV在性能和效率之间提供更好的平衡。这也有 助于减小驱动电机的尺寸，并实现对PEV动力总成系统中电气部件 的过载保护。对于传统多速变速器，通常需要电控离合器来确保换 挡过程的平顺性。然而，凭借电动机的快速精确响应及其多种工作 模式（即速度模式、扭矩模式和自由模式），离合器已不再必要， 可通过电动机的主动控制来保证换挡性能（刘等人，2012）。由于 内燃机的主动控制已在传统车辆中用于无离合器换挡，集中式电机 驱动PEV可以毫无问题地取消离合器装置。通过电机的主动控制， 换挡性能不仅可得到保障，甚至还能得以提升。

电动驱动电机具有快速动态特性，因此在电驱动系统中容易出 现振荡（Caruntu等人，2013）。对于智能机械变速器（IMT） 动力传动系统而言，由于无离合器结构，振荡阻尼控制更具挑战性。
此外，在现代车辆中，控制器的控制信号和传感器的测量值均通过 控制器局域网（CAN）进行交换，受限于带宽，IMT动力总成系统 中不可避免地会出现网络诱导随机延迟（帅等人，2014）。这些时 变延迟可能降低控制系统的性能，甚至导致闭环系统失稳，为传动 系统振荡阻尼控制带来了额外挑战，这一点在IMT动力总成系统的 控制中已得到充分关注。

在实际车辆动力传动控制系统中，传感器通常以时间驱动模式 工作，而变速器控制单元（TCU）、电机控制单元（MCU）和电 机则以事件驱动模式工作（Caruntu等，2013）。时间驱动的传 感器以固定的采样时间周期性执行。如果假设控制系统中的所有节 点（包括控制器节点和执行器节点）均采用时间驱动工作模式，则 对于时间驱动的

246电动车辆的建模、动力学与控制
工作模式仅为默认采样周期的整数倍数（史和余，2011）。然而， 在事件驱动模式下，当传感器节点的测量值到达控制器或执行器节 点时，控制信号将立即被触发。由于网络诱导时变延迟，MCU和电 机在每个简单周期内的控制信号可能会耦合，这将给IMT动力总成 系统的离散时间模型引入非线性不确定性，并为控制器设计带来额 外挑战（比宾加尔和金，2013）。由于网络诱导时变延迟通常是< 有界的>，因此在鲁棒控制方法中将其不确定性建模为具有有限顶点 的多面体是可取的（张等，2014）。然而，由于这些不确定性是与 延迟相关的非线性项，多面体包含方法无法直接使用。因此，可以 采用泰勒级数展开进行线性化处理（赫特尔等，2006）。

在IMT动力总成系统的振荡阻尼控制中，包括空气动力阻力扭 矩、滚动转矩和阻力转矩在内的负载转矩无法被精确建模，这容易 给控制系统带来外部干扰，需通过适当的鲁棒控制器设计进行抑制。
在干扰衰减的鲁棒控制中，通常有能量到能量控制、能量到峰值控 制和峰值到峰值控制（张等，2014）。由于瞬态响应在IMT动力总 成系统的振荡阻尼控制中具有重要意义，因此能量到峰值控制是一 个合适的选择，该方法可将受控输出的无穷范数限制在一定水平内 （高等，2006）。

在本章中，针对IMT动力总成系统提出了一种鲁棒振荡阻尼控 制方法。本工作的主要贡献如下：（1）以电子控制单元（ECU） 和执行器在事件驱动模式下工作为基础，在IMT动力总成系统的控 制器设计中考虑了网络诱导时变延迟；（2）采用基于泰勒级数展 开的多面体包含技术，处理IMT动力总成控制系统中由网络诱导时 变延迟引起的非线性不确定性；（3）应用鲁棒能量到峰值控制， 以确保IMT动力总成系统的瞬态响应；（4）控制律基于多变量比 例积分（PI）控制，可确保提出的控制器在实际动力总成控制系统 中的适用性和性能。

247电动汽车传动系统设计与控制

7.2 配备IMT动力总成系统的电动汽车

典型的IMT动力总成架构在电动汽车中的示意图如图7.1所示。驱动 电机直接与变速器相连，无需离合器。采用CAN总线实现电机控制 单元（MCU）与变速器控制单元（TCU）之间的通信。因此， MCU可以随时接收并响应来自TCU的转速和扭矩指令。换挡过程 包括齿轮释放和齿轮啮合，由变速器执行机构控制完成，执行机构 可以是直流电机，也可以是带电磁阀的气动缸。车辆控制系统中还 包括其他一些控制单元，如车辆管理系统（VMS）、电池管理系统 （BMS）等。同样，所有这些控制单元相互连接并能够相互通信。
因此，如所示，驾驶员输入的信息可由VMS采集，并与其他控制单 元共享（朱等人，2015ad）。

所提出的IMT系统的工作原理可以总结为：（1）TCU首先根 据加速信息、制动信号、当前电机转速和车速计算出适当的换挡级 别和目标电机转速值；（2）目标转速以及电机的工作模式需求将 被发送至MCU；（3）MCU将响应这些控制信号以调节电机的输 出转速和扭矩，同时变速器执行机构将被激活以完成换挡操作； （4）当换挡过程完成后，TCU将向MCU发送扭矩恢复请求，并等 待下一个换挡指令。

248电动车辆的建模、动力学与控制

7.2.1 换挡控制策略分析

考虑包含无离合器AMT的IMT动力总成系统。由于动力总成系统中 没有离合器，必须实时调节驱动电机的转速和扭矩。电机的工作模 式包括速度模式、自由模式和扭矩模式，由变速器控制单元确定。
在速度模式下，通过闭环控制使转速达到目标值。在扭矩模式下， 输出扭矩根据踏板信号进行调节。在自由模式下，电机无输出扭矩 自由运转。表7.1显示了不同换挡阶段中电机的工作模式及其控制策 略。

根据当前车速和踏板位置信号，变速器控制单元依据预定义换 挡规则做出换挡决策，并在不同的换挡阶段改变电机的状态。
IMT系统的换挡过程可分为预换挡阶段、脱挡阶段、调速同步阶段、 挂挡以及扭矩恢复阶段。具体的换挡过程如下。

在预换挡阶段，电机工作在扭矩模式下。TCU向VMS发送换挡 请求，并在获得许可后接管其控制权。在进入脱挡阶段之前， TCU通过向MCU发送指令，控制电机切换至自由模式。随后，在 MCU的控制下，电机将自由旋转并实现零扭矩输出。TCU将接收 来自MCU的消息，以确认电机已处于自由模式，然后操控执行器 进行脱挡操作。当脱挡部件到达目标位置（空档位置）时，脱挡阶 段结束。

档位完全释放后，启动调速同步阶段。TCU控制电机切换至速 度模式，并向MCU发送目标电机转速。电机转速与

换挡阶段	电机模式	控制策略
预换挡 齿轮释放 同步	扭矩模式 自由模式	TCU接管车辆的控制 来自VMS
齿轮啮合	速度模式	TCU向MCU发送目标速度
扭矩恢复	自由模式 扭矩模式	TCU控制执行器进行齿轮啮合 变速器控制单元向电机控制单元发送扭矩请求

当前电机转速和目标电机转速由变速器控制单元实时判断。在变速 器控制单元的监控下，电机控制单元将快速调整电机转速。当转速 差被调节至可接受范围内并维持一定时间后，同步阶段完成，变速 器控制单元将准备进入换挡啮合阶段。

在进入挂挡阶段之前，TCU会首先请求电机再次切换到自由模 式。与齿轮释放类似，TCU将收到来自MCU的确认后，操控执行 器进行齿轮啮合。挂挡阶段完成后，电机将根据TCU的请求工作在 扭矩模式。为了使冲击度保持在可接受范围内，TCU将根据踏板信 号向MCU发送扭矩恢复请求。当电机输出扭矩恢复后，整个换挡 过程结束，TCU将把控制权交还给VMS。基于以上分析，整体换挡 控制策略如图7.2所示。

250电动车辆的建模、动力学与控制

7.2.2 换挡动态分析

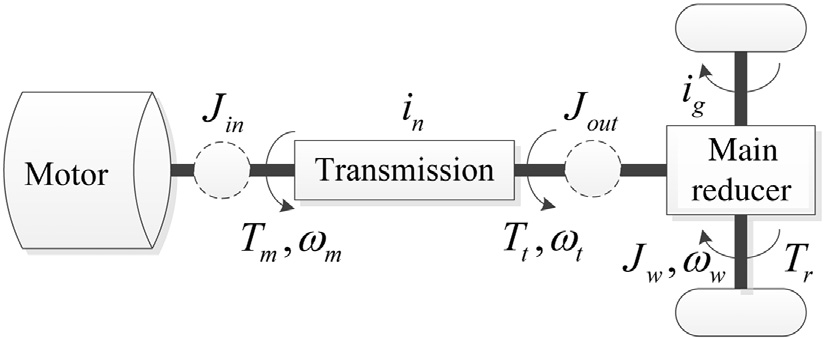
以无离合器AMT系统为例，图7.3展示了电动汽车中一个简化 的IMT动力总成系统，其中Fig. 7.3，J in和J out分别为折算到输入轴 和输出轴的转动惯量；Tm为电机扭矩； ωm为输入轴旋转速度，等 于电机转速；in为当前齿轮比；Tt为传递到变速器输出轴的扭矩；
ωt为输出轴的旋转速度；ig为主减速器传动比； ωw为车轮速度；J
w为车轮转动惯量；且Tr为外部阻力扭矩（Zhu et al.,2015ad）。

在换挡请求前阶段，齿轮保持在变速器中啮合。电机转速ωm 与输出轴速度 ωt成正比，比例为当前传动比in；而输出轴速度 ωt
与车轮速度ωw成正比，比例为最终减速比ig。该阶段简化的IMT动 力总成系统的动力学方程如下：

$$
J_{in}\dot{\omega} m = T_m - \frac{T_t}{i_n} \
J {out}\dot{\omega} t = T_t - \frac{T_r}{i_g} \
T_r = T {roll} + T_{grad} + T_{airdrag} \
T_{roll} = C_r m_v g \cos(\alpha) r_w, \quad T_{grad} = m_v g \sin(\alpha) r_w, \quad T_{airdrag} = \frac{1}{2} \rho_{air} A_f C_d V_v^2 r_w, \quad V_v = r_w \omega_w
$$

(7.1)
其中，Cr为滚动阻力系数，mv为车辆质量，α为道路坡度，rw为 车轮半径， ρair为空气密度，Af为车辆迎风面积，Cd为空气动力 阻力扭矩系数，Vv为车速。外部阻力扭矩Tr由空气阻力扭矩Tairdrag、 滚动转矩Troll以及由道路坡度引起的Tg rade组成。

当档位释放时，包括调速同步阶段，输入轴与输出轴之间没有 连接。IMT动力总成的动态方程为：

251电动汽车传动系统设计与控制

$$
J_{in}\dot{\omega}_m = T_m \
J_v\dot{\omega}_w = - T_r \
J_v = J_w + m_v r_w^2
$$

(7.2)
其中，Jv 是车辆惯量，可通过将车轮的惯量Jw 与车辆质量mv的等效惯 量相加得到。

不良的齿轮释放或接合可能导致换挡冲击，从而影响换挡质量。
换挡冲击通常通过车辆纵向加速度变化率来评估（赵等人，2014a c）。为了减小换挡冲击，应尽可能降低输出扭矩Tt，这就要求电 机具备快速模式切换能力，即从速度模式或扭矩模式切换到自由模 式（刘等人，2012）。同时，转速同步必须既高效又有效。

7.2.3 速度同步分析

换挡持续时间是直接影响换挡质量的一个重要指标。由于IMT系统
中没有离合器，换挡质量更依赖于转速同步控制。根据Liu et al.
(2012)的实验结果，无离合器AMT系统的转速同步过程占总换挡时 间的一半。除了时间因素外，还需要鲁棒转速同步以确保良好的换 挡啮合性能。由于车辆惯量值相对较大，在调速同步阶段车轮速度 可视为恒定值（钟等人，2012）。然而，这一假设要求转速同步过 程的持续时间非常短。因此，必须保证转速同步控制系统的瞬态性 能。在转速同步过程中，当前电机转速与目标电机转速之间的转速 差可描述为：

$$
\Delta\omega = \omega_{m,t} - \omega_m = \omega_w \cdot i_g \cdot (i_{n+1} - i_n)
$$

(7.3)
其中 ωm_t为目标电机转速， ωm为当前电机转速， ωv为车轮速度，ig
为主减速器传动比，in11为待啮合挡位传动比，in为当前挡位传动比。
从公式(7.3)可以很容易看出，在升挡过程中，in11, in，当前电机 转速快于目标电机转速。为了确保平顺换挡，需要将电机转速降低
Δω首先。而对于降挡过程，in11.in，电机转速应增加Δω。

7.3 问题表述

IMT动力总成系统的网络化控制结构如图7.4所示。电机转速和车 轮转速由传感器直接测量，而由于直接测量的复杂性和成本问题， 扭角或扭矩必须通过估计获得。TCU根据来自控制器局域网的测量 值以及参考车速，在每次测量数据通过控制器局域网到达时计算所 需扭矩。类似地，电机控制单元将根据控制器局域网的指令驱动电 机产生期望扭矩或转速。因此，在IMT动力总成系统的控制系统中， 变速器控制单元相当于上层控制器，而电机控制单元则为下层控制 器。可以看出，外部负载扭矩Trr以及网络诱导延迟τk是整个控制 系统的主要不确定性因素，这些因素将在IMT动力总成系统的振荡 阻尼控制器设计中被充分考虑（朱等人，2015ad）。

7.3.1 IMT动力总成系统控制建模

电机‐变速箱和车轮‐车辆动力学通常被建模为集中惯量系统（傅等 人，2011）。基于公式(7.1)中的动力学分析，IMT动力总成系统的 微分方程可写为：

$$
J_m\dot{\omega} m = T_m - \frac{T_g}{i} - c_m\omega_m \
J_g\dot{\omega}_g = T {go} - T_f \
J_v\dot{\omega} w = T_f - T {load} \
T_f = c_f (\omega_g - \omega_w) + k_f (\theta_g - \theta_w)
$$

(7.4)
当传动齿轮保持啮合时，可得到以下关系：

$$
T_{go} = i_g i_0 T_g i, \quad \omega_m = i_g i_0\omega_g, \quad \theta_m = i_g i_0\omega_g
$$

(7.5)
因此，IMT动力总成系统的动态模型可以简化为：

$$
J_{mg}\dot{\omega} m = T_m - \frac{T_f}{i_n i_g} - c_m\omega_m, \quad J {mg} = (J_m + J_g/i_n^2 i_g^2) \
J_v\dot{\omega}_w = T_f - T_r \
T_f = c_f (\omega_m/i_n i_g - \omega_w) + k_f (\theta_m/i_n i_g - \theta_w)
$$

(7.6)
对于任意期望车轮转速 ω w，可根据公式(7.3)得到电机转速、扭 转变形角和电机扭矩的稳态值：

$$
\omega^ _m = i_g i_0 \omega^ _w \
\theta^ _m/i_g i_0 - \theta^ _w = T^ _r/k_f \
T^ _m = c_m i_g i_0 \omega^ _w + T^ _r/i_g i
$$

(7.7)
为了处理外部负载扭矩中的非线性项Tload，采用线性近似方法（ Caruntu等人，2013）：

$$
T’_{airdrag} = c_a \omega_w
$$

(7.8)
其中ca是一个近似参数。T0
airdrag
被用于控制器设计过程中，并通过 使用鲁棒控制设计消除模型误差的影响。

以电机扭矩作为控制输入，状态变量选择为：

254电动车辆的建模、动力学与控制

$$
x_1 = \omega_m - \omega^ _m \
x_2 = \omega_w - \omega^ _w \
x_3 = (\theta_m/i_g i_0 - \theta_w) - (\theta^ _m/i_g i_0 - \theta^ _w)
$$

(7.9)
基于公式(7.2)(7.7)，IMT动力总成系统的状态空间模型可以描 述为：

$$
\dot{x} = Ax + B(u - u^*) + d \
x = \begin{bmatrix} x_1 \ x_2 \ x_3 \end{bmatrix}, \quad A = \begin{bmatrix}
-\frac{c_m}{J_{mg}} & -\frac{c_f}{i_g^2 i_0^2 J_m} & \frac{c_f}{i_g i_0 J_{mg}} \
-\frac{k_f}{i_g i_0 J_{mg}} & \frac{c_f}{i_g i_0 J_v} & -\frac{c_a + c_f}{i_g i_0 J_v} \
\frac{k_f}{J_v} & 1 & -1 \
0 & 0 & 0
\end{bmatrix}, \quad B = \begin{bmatrix} \frac{1}{J_{mg}} \ 0 \ 0 \end{bmatrix}
$$

(7.10)

第7章 传动系统设计和电动汽车控制（续）

7.3 问题表述（续）

7.3.2 网络诱导时变延迟建模

IMT动力总成控制系统中的网络诱导时变延迟如图7.5所示。来自 传感器节点的测量值s以固定的采样周期Ts周期性生成。当测量值 s(k)通过CAN在时间t7,到达TCU节点时，事件驱动的TCU节点将立 即执行，并使用该测量值计算作为控制信号的所需扭矩uk。类似地， 当控制信号通过CAN到达时，MCU和电机节点将把该扭矩施加到 动力总成系统上

控制信号通过CAN到达时。由于CAN引起的延迟{s(k)的 τk和 s(k+1)的 τk11，扭矩uk将在时间t8开始起作用，并在时间t10结束。
基于上述分析，具有CAN引起的时变延迟的IMT动力总成系统 (7.10)的控制输入可以描述如下：

$$
\tilde{u}(t) = u_k, \quad \forall t \in [t_k + \tau_k, t_{k+1} + \tau_{k+1}] \
\tilde{u}(t) = u - u^*, \quad t_k = kT_s
$$

(7.11)
其中，Ts是采样周期， τk表示网络在第k步引起的延迟。
可以合理地假设CAN引起的延迟通常是有界的。在不失一般 性的前提下，最大延迟可表示为：

$$
\tau_{large} = (\Upsilon + \upsilon)T_s \
\Upsilon \in \mathbb{Z}^+, \quad \upsilon \in \mathbb{R}[0,1)
$$

(7.12)
根据控制器局域网协议，同一ID组内的消息会被排队，并且会 重新发送直到被接收。因此，在某一时刻发送的消息永远不可能比 之前时刻发送的消息先到达，如下所示：

$$
\tau_k \geq \tau_{k-1} - T_s
$$

(7.13)
由于网络诱导随机延迟，在一个采样周期内可能会有多个有效 控制信号起作用。以采样周期kTsB(k11) Ts为例，从图7.5可以看 出，控制信号uk22、uk21和uk将在该周期内依次被添加到IMT动力 总成系统中。因此，具有网络诱导延迟的IMT动力总成系统的离散 模型描述如下：

$$
x(k+1) = A_1x(k) + B_1u(k) + E_1d(k) + \Delta_{0,k}(u(k-1) - u(k)) \
+ \Delta_{1,k}(u(k-2) - u(k-1)) + \cdots + \Delta_{\Upsilon,k}(u(k-\Upsilon-1) - u(k-\Upsilon))
$$

(7.14)
其中
$$
A_1 := e^{AT_s}; \quad B_1 := \int_0^{T_s} e^{A(T_s - \theta)} d\theta B; \quad E_1 := \int_0^{T_s} e^{A(T_s - \theta)} d\theta I \
\Delta_{i,k} :=
\begin{cases}
0, & \tau_{k-i} - iT_s \leq 0 \
\int_0^{\tau_{k-i} - iT_s} e^{A(T_s - \theta)} d\theta B, & 0 \leq \tau_{k-i} - iT_s \leq T_s \
\int_0^{T_s} e^{A(T_s - \theta)} d\theta B, & T_s \leq \tau_{k-i} - iT_s
\end{cases}
$$

由公式(7.12)到(7.14)可知，必须首先获得网络诱导延迟的上界， 才能确定IMT动力总成系统的离散模型。根据现有理论研究（帅等 人，2014）中关于汽车应用中CAN引起的延迟上界的计算方法，可 采用以下表达式：

$$
\tau_{large,j} \leq \frac{(j + 2)l}{R} - \sum_{i=0}^{j-1} \frac{l}{c_i}
$$

(7.15)
其中τlarg e,j是优先级j的CAN消息的最大延迟，l表示最大帧长度， R是高速CAN的速率，ci是优先级i的消息的周期长度，表示消息重 复的周期。
根据公式(7.15)计算得到的上界，可应用多面体包含法。然而， 由公式(7.14)可以看出，控制矩阵，即Δi,k，与时变延迟τk具有非线 性关系，通常需要对这些控制矩阵进行线性化。因此，采用泰勒级 数展开法来近似非线性项Δi,k。系统控制矩阵中的积分项定义为：

$$
\Delta(x) = \int_0^{T_s} e^{A(T_s - \theta)} d\theta
$$

(7.16)
可以将其线性化为：

$$
\Delta(x) = \Delta(0) + \dot{\Delta}(0)x + \ddot{\Delta}(0)\frac{x^2}{2} + \cdots + \frac{d^n\Delta(0)}{dx^n}\frac{x^n}{n!} \
= \sum_{n=1}^{h} \frac{(-1)^{n+1}}{n!} A^{n-1} e^{AT_s} x^n + \text{h.o.t}
$$

(7.17)
其中h是选定阶数，足以表示 Δ(x)中的非线性项。h.o.t表示高阶项， 因其值很小可忽略不计。
由于 Δ(0)=0，选定阶数为h时，公式(7.17)可进一步改写为：

$$
\Delta(x) = A_\tau x_\tau \
A_\tau = e^{AT_s} \left[ \frac{(-1)^2}{1!} A^0 \quad \frac{(-1)^3}{2!} A^1 \quad \cdots \quad \frac{(-1)^{h+1}}{h!} A^{h-1} \right] \
x_\tau = \left[ x \quad x^2 \quad \cdots \quad x^h \right]^T
$$

(7.18)
根据公式(7.12)(7.14)的分析，积分变量在任何时变延迟 τk下 都只会被限制在[0,Ts]或[0,υTs]内。因此，由控制器局域网引起的 时变延迟多面体的顶点可定义为：

$$
x_{\tau;j,0} = \left[ x_\tau \quad x_\tau^2 \quad \cdots \quad x_\tau^h \right]^T \
x_{\tau;j,1} = \left[ x_{\tau,j} \quad x_{\tau,j}^2 \quad \cdots \quad x_{\tau,j}^h \right]^T \
\vdots \
x_{\tau;j,h} = \left[ x_{\tau,j} \quad x_{\tau,j}^2 \quad \cdots \quad x_{\tau,j}^h \right]^T, \quad j = 0,1, \quad x_\tau = 0, \quad x_{\tau,0} = T_s, \quad x_{\tau,1} = \upsilon T_s
$$

(7.19)
因此，控制矩阵的凸多面体的顶点，即Δi,k可以表示为：

$$
\hat{\Delta} {0,n} = A \tau x_{\tau,0,n} B, \quad \hat{\Delta} {1,n} = A \tau x_{\tau,1,n} B \
\forall n = 0,1,\ldots,h
$$

(7.20)
最后，对于任何由控制器局域网引起的延迟 τk，公式(7.14)中的 不确定控制矩阵可以描述为：

$$
\Delta_{i,k} = \sum_{n=0}^{h} \eta_{i,n}(k) \hat{\Delta} {1,n} B, \quad \forall i = 0,1,\ldots,\Upsilon-1 \
\Delta {i,k} = \sum_{n=0}^{h} \eta_{i,n}(k) \hat{\Delta} {0,n} B, \quad i = \Upsilon \
\sum {n=0}^{h} \eta_{i,n}(k) = 1
$$

(7.21)
其中ηi,n(k)是由控制器局域网引起的延迟τk以及在公式(7.19)中定义的 多面体的顶点所确定的时变系数公式(7.19)。

7.3.3 系统增广

通过多面体包含，不确定控制矩阵可以用时变延迟的线性表达式来描述。
系统增广

258电动车辆的建模、动力学与控制
该技术可用于处理系统中的耦合控制输入(7.14)。定义一个新的状态变 量为：

$$
X(k) = \left[ x^T(k) \quad u^T(k-1) \quad \cdots \quad u^T(k-\Upsilon-1) \right]^T
$$

(7.22)
然后，增广系统可以重写为：

$$
X(k+1) = A_2 X(k) + B_2 u(k) + E_2 w(k) \
A_2 = \begin{bmatrix}
A_1 & \Delta_{0,k} - \Delta_{1,k} & \cdots & \Delta_{\Upsilon-1,k} - \Delta_{\Upsilon,k} & \Delta_{\Upsilon,k} \
0 & 0 & \cdots & 0 & 0 \
0 & I & \cdots & 0 & 0 \
\vdots & \vdots & \ddots & \vdots & \vdots \
0 & 0 & \cdots & I & 0
\end{bmatrix} \
B_2 = \left[ B_1^T - \Delta_{0,k}^T \quad I \quad 0 \quad \cdots \quad 0 \right]^T \
E_2 = \left[ E_1^T \quad 0 \quad 0 \quad \cdots \quad 0 \right]^T
$$

(7.23)

7.4 振荡阻尼控制器设计

控制律设计为u(k)=KX(k)，增广系统可转换为：

$$
X(k+1) = (A_2 + B_2 K) X(k) + E_2 w(k)
$$

(7.24)
从式(7.9)的定义可以看出，电机转速跟踪误差、车轮速度跟踪 误差以及误差积分被选为状态变量。因此，增广系统式(7.24)的状 态反馈控制实际上等同于IMT动力总成系统原始动态模型的多变量 PI控制（郑等人，2002）。
车轮速度的跟踪误差被选为一个受控输出以评估跟踪性能，而 车轴扭振率被选为另一个控制器输入以显示动力总成系统的振荡：

$$
Z_1 = C_1 X, \quad C_1 = \left[ 0 \quad I \quad 0 \quad 0 \quad \cdots \quad 0 \right]
$$

(7.25)
其中ϒ+1个块。

$$
Z_2 = C_2 X, \quad C_2 = \left[ \frac{I}{i_g i_0} \quad -I \quad 0 \quad 0 \quad \cdots \quad 0 \right]
$$

(7.26)
其中ϒ+1个块。
为了确保IMT动力传动系统的振荡阻尼控制，采用峰值能量性 能来保证公式(7.23)所示系统的瞬态响应：

$$
|Z_1| \infty < \gamma_1 |w|_2, \quad |Z_2| \infty < \gamma_2 |w|_2
$$

(7.27)
状态反馈控制增益K将直接用于实际的动力总成控制系统中， 以实现期望的控制性能。由于在提出的控制器设计中已考虑了外部 干扰、建模误差和信号延迟，因此给出以下引理，以严格保证闭环 系统的稳定性以及能量到峰值性能。

引理1
(张等人，2013年)。闭环系统(7.24)在两个峰值能量性能指标γ1和 γ2
下是稳定的，如果存在正定对称矩阵P，使得以下矩阵不等式成立：

$$
\begin{bmatrix}
-P & P(A_2 + B_2 K) & PE_2 \
* & -P & 0 \
* & * & -I
\end{bmatrix} < 0
$$

(7.28)

$$
\begin{bmatrix}
-P & C_1^T \
* & -\gamma_1^2 I
\end{bmatrix} < 0
$$

(7.29)

$$
\begin{bmatrix}
-P & C_2^T \
* & -\gamma_2^2 I
\end{bmatrix} < 0
$$

(7.30)
证明：通过选择以下二次Lyapunov函数，可以完成稳定性的证明：

$$
V(k) = X^T(k) P X(k)
$$

(7.31)
当外部输入为零时，闭环系统(7.24)稳定当且仅当下列不等式成立：

$$
X(k+1)^T P X(k+1) - X(k)^T P X(k) < 0
$$

(7.32)
利用施尔补引理，由式(7.28)可知式(7.32)中的条件可以得到 保证。因此，闭环系统(7.24)是稳定的。对于峰值能量性能，式 (7.32)可重写为：

$$
\Delta V(k) = X(k+1)^T P X(k+1) - X(k)^T P X(k) \
= \begin{bmatrix} X(k) \ w(k) \end{bmatrix}^T \begin{bmatrix}
(A_2 + B_2 K)^T P (A_2 + B_2 K) - P & (A_2 + B_2 K)^T P E_2 \
* & E_2^T P E_2
\end{bmatrix} \begin{bmatrix} X(k) \ w(k) \end{bmatrix}
$$

(7.33)
为了证明峰值能量性能，定义以下成本函数：

$$
J = V(k) - \sum_{i=0}^{k-1} w^T(i) w(i)
$$

(7.34)
由于扰动w(k)在工程实践中是有界的，因此2式(7.34)可进一步改 写为：

$$
J = V(k) - \sum_{i=0}^{k-1} w^T(i) w(i) = V(k) - V(0) - \sum_{i=0}^{k-1} w^T(i) w(i) \
= \sum_{i=0}^{k-1} \Delta V(i) - \sum_{i=0}^{k-1} w^T(i) w(i)
$$

(7.35)
将式(7.33)代入式(7.35)，可得以下方程：

$$
J = \sum_{i=0}^{k-1} \begin{bmatrix} X(i) \ w(i) \end{bmatrix}^T \begin{bmatrix}
(A_2 + B_2 K)^T P (A_2 + B_2 K) - P & (A_2 + B_2 K)^T P E_2 \
* & -I + E_2^T P E_2
\end{bmatrix} \begin{bmatrix} X(i) \ w(i) \end{bmatrix}
$$

(7.36)
再次使用舒尔补，由式(7.36)可得

$$
J < 0
$$

(7.37)
因此条件(7.34)可进一步重写为：

$$
V(k) \leq \sum_{i=0}^{k-1} w^T(i) w(i)
$$

(7.38)
类似地，再次使用舒尔补，由式(7.29)至(7.30)可知

$$
C_1^T C_1 < \gamma_1^2 P
$$

(7.39)

$$
C_2^T C_2 < \gamma_2^2 P
$$

(7.40)
因此由式(7.25)、(7.38)和(7.39)可以看出

$$
Z_1^T(k) Z_1(k) = X^T(k) C_1^T C_1 X(k) \
\leq \gamma_1^2 X(k)^T P X(k) = \gamma_1^2 V(k) \leq \gamma_1^2 \sum_{i=0}^{k-1} w^T(i) w(i) \leq \gamma_1^2 \sum_{i=0}^{N} w^T(i) w(i)
$$

(7.41)
对于任意k > 0, w(k) \in l_2[0, N],式(7.41)等于：

$$
|Z_1|_\infty < \gamma_1 |w|_2
$$

(7.42)
采用类似的方法，$|Z_2|_\infty < \gamma_2 |w|_2$也可被证明。
引理1可确保闭环系统(7.24)的稳定性和峰值能量性能。然而， 由于存在双线性项P(A21BK)，无法直接应用该引理。为了解决这 一问题，提出了以下定理。

定理1 闭环系统(7.24)在两个能量到峰值性能指标γ1和 γ2下是稳定 的，如果存在矩阵 Ω^T = Ω、M、Y，使得以下矩阵不等式成立：

$$
\begin{bmatrix}
-\Omega & A_2 \Omega + B_2 Y & E_2 \
* & \Omega - M - M^T & 0 \
* & * & -I
\end{bmatrix} < 0
$$

(7.43)

$$
\begin{bmatrix}
-\Omega & \Omega C_1^T \
* & -\gamma_1^2 I
\end{bmatrix} < 0
$$

(7.44)

$$
\begin{bmatrix}
-\Omega & \Omega C_2^T \
* & -\gamma_2^2 I
\end{bmatrix} < 0
$$

(7.45)
反馈控制增益可以计算为：

$$
K = Y \Omega^{-1}
$$

(7.46)
证明：对公式(7.43)进行diag{I, M^{-1}Ω, I}的合同变换，可得公式(7.43)中 的条件可以推导出：

$$
\begin{bmatrix}
-\Omega & (A_2 + B_2 K) \Omega & E_2 \
* & P^T \Theta P & 0 \
* & * & -I
\end{bmatrix} < 0
$$

(7.47)
其中 Θ = (M^{-1})^T Ω M^{-1} - (M^{-1})^T - M^{-1}。
通过使用不等式(P - M^{-1})^T P^{-1} (P - M^{-1}) \geq 0，可以得到以下条 件：

$$
\Theta \geq -P
$$

(7.48)
因此条件(7.47)可以进一步变为

$$
\begin{bmatrix}
-\Omega & (A_2 + B_2 K) \Omega & E_2 \
* & -\Omega & 0 \
* & * & -I
\end{bmatrix} < 0
$$

(7.49)
对公式(7.49)进行diag{Ω^{-1}, Ω^{-1}, I}的合同变换后，条件(7.49)可转 换为：

$$
\begin{bmatrix}
-\Omega^{-1} & \Omega^{-1}(A_2 + B_2 K) & \Omega^{-1} E_2 \
* & -\Omega^{-1} & 0 \
* & * & -I
\end{bmatrix} < 0
$$

(7.50)
由于 Ω^{-1}也是一个正定对称矩阵，且条件(7.50)等价于条件
(7.28)。类似地，对公式(7.44)和(7.45)应用diag{Ω^{-1}, I}的合同变换 后，条件(7.29)和(7.30)成立。
由于引理1中的双线性项已被消除，因此可以利用线性矩阵不 等式(LMI)工具箱获得反馈控制增益。然而，定理1中存在两个性能 指标γ1和 γ2。希望在具有满意的跟踪性能的情况下

263电动汽车传动系统设计与控制
车轮速度缠绕速率应尽可能小，以减少抖动效应。为了平衡这 些性能，建立了以下优化问题。

推论1 ：在给定水平γ1的情况下，可通过求解以下最小化问题来获得 最小的峰值能量性能指标γ2 ：

$$
\min \gamma_2^2 \
\text{s.t.} \
\begin{bmatrix}
-\Omega & A_2 M + B_2 Y & E_2 \
* & \Omega - M - M^T & 0 \
* & * & -I
\end{bmatrix} < 0 \
\begin{bmatrix}
-\Omega & \Omega C_1^T \
* & -\gamma_1^2 I
\end{bmatrix} < 0 \
\begin{bmatrix}
-\Omega & \Omega C_2^T \
* & -\gamma_2^2 I
\end{bmatrix} < 0
$$

(7.51)
在增广系统(7.23)中，存在(ϒ+1)个不确定性项，即Δ0k, Δ1k,…,
Δϒ,k，针对系统矩阵。此外，每个不确定性通过使用 n阶泰勒级数 展开进行线性化。因此，需要一个具有(ϒ+1)n+1个顶点的凸多面体 来表示每个时变网络诱导延迟。为了确保采用多面体包含方法建模 的IMT系统的稳定性以及峰值能量性能，进一步推导条件(7.43)如下：

$$
\begin{bmatrix}
-\Omega & A_{2,i} \Omega + B_{2,i} Y & E_2 \
* & \Omega - M - M^T & 0 \
* & * & -I
\end{bmatrix} < 0 \
\forall i = 1,2,\ldots,(h+1)^{n+1}
$$

(7.52)
需要注意的是，条件(7.52)中所有矩阵不等式共享同一个Y， 这意味着控制器中仅采用一个反馈增益K 。与增益调度方法（张等，
2014）相比，使用固定控制增益可能略显保守。然而，可以避免ηi,n
(k)在公式(7.21)中的在线计算。由于控制增益K是固定的，可离线 计算，因此该控制器能更方便地应用于具有保证性能的实际动力总 成系统。

264电动车辆的建模、动力学与控制

7.5 仿真结果

在MATLAB/Simulink中进行了仿真，以评估所提出的控制器的性 能，其中采用传统PI控制器进行对比分析。IMT动力总成系统的参 数值来自现有研究（Caruntu等人，2013；Raisemche等， 2014），如表7.2所列。

设计的仿真平台如图7.6所示，包括动力总成模块、TCU模块、 电机控制单元和电机模块，以及网络模块。根据参考车速信号和动 力总成系统的测量值，TCU将计算出期望扭矩指令。在电机控制单 元和电机的配合下，实际扭矩将根据这些指令施加到动力总成动态 系统上。控制系统中的时变延迟将由网络模块产生。
考虑到执行器的物理限制，在仿真框图中采用了饱和函数来限 制电机扭矩、电机扭矩变化率、电机转速以及车轮速度。这些物理 限制描述如下（Caruntu等人，2013）：

$$
0 \leq T_m \leq 160 \, \text{Nm}, \quad 0 \leq \dot{T}_m \leq 2.5 \, \text{Nm}, \
0 \leq \omega_m \leq 523.6 \, \text{rad/s}, \quad 0 \leq \omega_w \leq 247.1 \, \text{rad/s}
$$

(7.53)

265电动汽车传动系统设计与控制
最大网络诱导延迟设置为1.7Ts，而变速器控制单元的采样周期 选择为Ts= 0.01s。假设网络诱导延迟是时变且均匀分布的，如图 7.7所示。在固定采样周期Ts下，0.1s内的时变延迟进一步显示在 图7.8中。

当选择峰值能量性能γ1为0.1时，获得的最小峰值能量性能γ2
为0.44。在给定车速的情况下，还使用仅基于速度误差的传统PI控 制来进一步显示所提出的控制器的优越性。首先假设控制器局域网 中不存在网络诱导延迟。进行一个加速场景，车辆从7km/h加速到 30km/h。使用传统PI控制器和提出的控制器时，速度跟踪性能如 图7.9所示。

由图7.9可以看出，两种控制器的车速跟踪性能均相当良好。
经过对PI控制增益进行仔细调节后，传统PI控制器可以获得与提出 的控制器几乎相同的性能。两种控制器的状态稳态误差可忽略不计， 且几乎没有超调。
车轴扭振率，即电机转速除以齿轮比与车轮速度之间的差值， 在图7.10中显示。在前1.2秒内，两个控制器的振荡几乎相同，由于 突然的加速操作，在启动阶段出现了相对较大的振荡。此后，两个 控制器均出现超调，且提出的控制器的超调甚至略大一些

266电动车辆的建模、动力学与控制
与传统PI控制器相比，使用提出的控制器时车轴扭振率为零，而使 用传统PI控制器时仍持续振荡。由于车轴扭振率直接与扭矩变化率 相关，并进一步影响动力总成的抖动，
这些稳态振荡是不希望出现的，可能会导致传动系统部件过度磨损，并降 低驾驶性能。
图7.11显示了传动轴扭矩响应，也可用于反映动力总成系统的 振荡情况。在约1.6秒时，传统PI控制器产生的超调量大于所提出控 制器的超调量，车辆乘客更容易感受到。
电机扭矩如图7.12所示，其中传统PI控制器导致控制输入在稳 态时出现轻微超调并持续振荡。而使用提出的控制器时，电机扭矩 输入将更加平滑。这些扭矩输入中的振荡会增加电机以及MCU的 负担，在实际动力总成控制系统中应予以避免。因此可以看出，尽 管两种控制器在车辆速度跟踪性能上几乎没有差异，但提出的

267电动汽车传动系统设计与控制
控制器在动力总成系统的振荡阻尼方面表现出更好的性能。
根据上述仿真结果，在理想网络条件下，提出的控制器与传统 PI控制器的整体性能差异并不明显。然而，当控制器局域网中开始 出现图7.7所示的时变延迟时，提出的控制器显示出其优越性。
图7.13展示了在网络诱导时变延迟下的车辆速度跟踪性能。可 以看出，尽管存在这些不利的延迟，提出的控制器仍能保持良好的 速度跟踪性能，而传统PI控制器在理想网络条件下也无法维持其良 好性能。由于随机的网络诱导延迟，采用传统PI控制器的IMT控制 系统的最大稳定区域将受到显著影响，实际车速会在期望值附近波 动。

268电动车辆的建模、动力学与控制
网络诱导时变延迟下的缠绕速率如图7.14所示。在前1.2秒内， 传统PI控制器和提出的控制器的性能相同。然而，使用传统PI控制 器时，角速度差在稳态期间持续振荡，由于不希望的信号延迟，其 跟踪能力几乎丧失。而对于提出的控制器，则保持了良好的阻尼性 能。提出的控制器的鲁棒性明显。
在传动轴扭矩响应中也可以观察到相同的情况，如图7.15所示。
由于网络诱导延迟，传统PI控制器会在传动轴扭矩中引起严重振荡， 乘客能够明显感觉到。而对于提出的控制器，传动轴扭矩响应几乎 不存在振荡。即使存在网络诱导延迟，仍可保持良好的传动轴扭矩 阻尼性能。电机扭矩响应如图7.16所示，可视为该

269电动汽车传动系统设计与控制
动力总成动态系统。同样，尽管存在随机信号延迟，提出的控制器 仍能保证电机的平稳的电机扭矩需求。而对于传统PI控制器，电机 扭矩响应中会出现持续的振荡。这些电机扭矩中的振荡非常严重， 可能会对MCU和电机中的电子元件造成损坏。

7.6 结论

本章针对集成电机传动（IMT）动力总成系统，提出了一种鲁棒峰 值能量控制器，以在网络诱导时变延迟和不确定的外部阻力矩存在 的情况下，保持车辆速度跟踪性能以及抑制振荡的能力。在IMT动 力总成控制系统中的电子控制单元（ECU）和执行器工作于事件驱 动模式时，采用基于泰勒级数展开的多面体包含技术来处理由这些 网络诱导时变延迟引起的非线性不确定性。通过使用系统增广技术 将原始动态模型转化为无延迟模型，并选择能量到峰值性能指标以 确保所提出的控制器的鲁棒性。所提出控制器采用的控制律基于多 变量PI控制，其控制增益通过LMI工具箱获得。通过一个加速场景 验证了所提出控制器的有效性。与传统PI控制器相比，该提出的控 制器不仅在理想网络条件下具有良好的速度跟踪性能，而且具备优 异的振荡抑制能力。当
当网络诱导时变延迟开始出现时，传统PI控制器可能导致动力总成 系统产生严重振荡；然而，由于该控制器的鲁棒性，提出的控制器 仍能保持良好的性能。
资助
本工作受到国家自然科学基金委员会（资助号51605278和51505276） 的支持。