刷题笔记 leetcode 704.二分查找(简单)

题目

给定一个 n 个元素有序的（升序）整型数组 nums 和一个目标值 target ，写一个函数搜索 nums 中的 target，如果目标值存在返回下标，否则返回 -1。

示例 1:

输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4

示例 2:

输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1

提示：

• 你可以假设 nums 中的所有元素是不重复的。

• n 将在 [1, 10000]之间。

• nums 的每个元素都将在 [-9999, 9999]之间。

来源：力扣（LeetCode）

链接：https://leetcode.cn/problems/binary-search

著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

方法

题目说到nums为升序数组（有序）数组，且所有元素不重复。如果数组是非有序的，则二分查找失效；数组元素重复的话返回下标不唯一。因此该题适合采用二分查找的方法。

二分查找大家都不陌生，但是涉及到很多容易让人搞混的边界条件。例如while(left<right)还是left<=right?二分时更新左右边界值是right=mid还是right=mid-1?这些在实际写代码时都是需要考虑的问题。

我在写题的时候也遇到了这样的困惑，总结为两种情况：

• 左闭右闭 即[left,right]

• 左闭右开 即[left,right)

左闭右闭 [left,right]

该区间意为我们要找的target目标值就在我们所定义的区间[left,right]之间，所以有下面两点：

while(left<=right)要使用<=符号，因为left==right是能够实际取到的。

if(nums[mid]>target) right的重新赋值需要令right=mid-1 ，因为此时右区间是闭合的，所以target必不可能等于nums[right],下一个要考虑到右边界值为mid-1。

对应代码

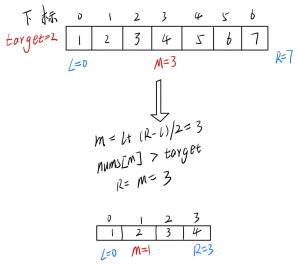
左闭右开[left,right)

该方法和上面方法不同根源之处就是右边为开区间，也就是right是取不到的，下面两点与第一种方法区别如下：

while(left<right) 这里不能为等号 因为开区间中right循环时是取不到该值的。

if(nums[mid]>target) right取值为mid 因为当前nums[mid]>target 去左侧区间继续循环，而左侧区间为左闭右开区间，所以right更新为mid 即下一个查询区间不会查询nums[mid]。

对应代码:

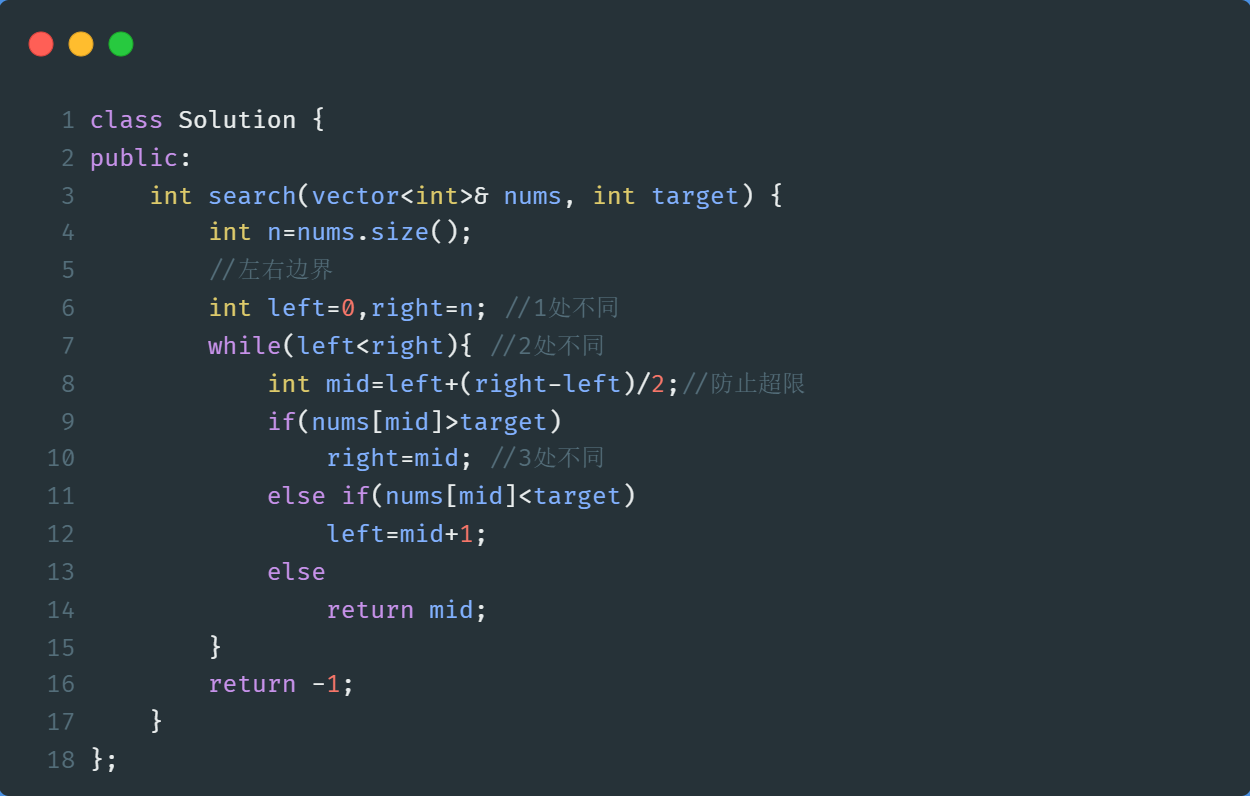
实际上，根据大部分人的代码习惯，左闭右闭的查找方法是最多的，也是最贴合下标的。

时空复杂度

时间复杂度：经典二分查找 O(logn)

空间复杂度：O(1)