数字矩阵

数字矩阵 输出N*N的数字旋转方阵 首先我们先定义一个二位数组 int a [N][N];

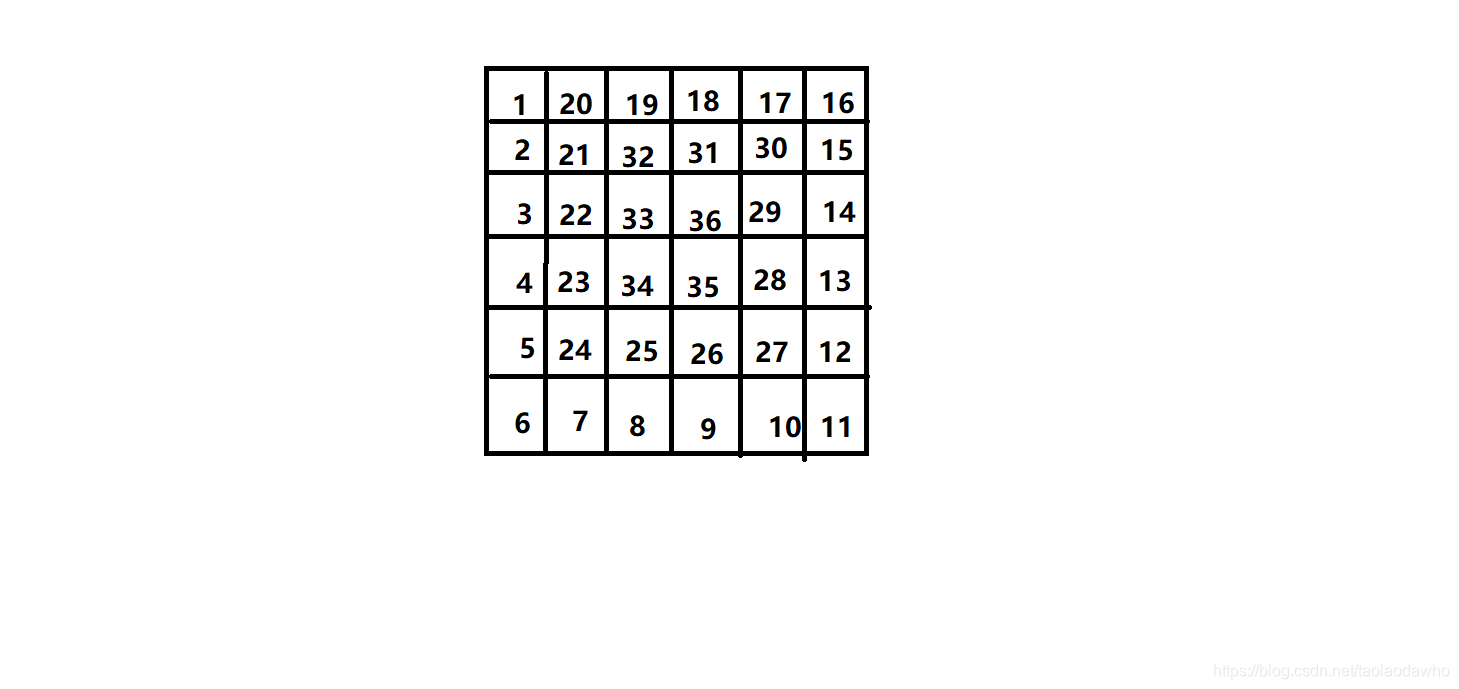
我们很明显的能够看出规律，最外层 依次从1~20 第二层依次从21 ~32 第三层从 33 ~ 到36，如何程序描述这个呢？首先我们把问题拆分一下先实现最外层 ，，每一层都有四个条边组成，而且相邻两个边（导致有一个点重合）所以我，我们让第一层每 每条边赋值N-1个点 最外层实际有（N-1）*4个点从（0，0）开始， 第二层从（1，1）有(N-3)*4 对相信各位朋友都有了想法了 我们中的两种方法意思都是一样的，希望可以给带来帮助大家

#include<stdio.h>
#define N 10 //必须是方阵
int a[N][N];
int count=0;
int print(){
for(int i=0;i<N;i++){
for(int j=0;j<N;j++){
printf("%d\t",a[i][j]);
}
printf("\n");
}
}
int fun(int pos ,int s){//我觉得算法题最重要的是自己的思维 很多时候我们能够发现数据之间的规律
if(s0){
return 0;
}
if(s1){ //当N为奇数的时候最内的一层为只有一个点
a[pos][pos]=++count;
return 1;
}
int i=pos,j=pos;// 每一层开始的起点
for(i;i<s-1+pos;i++){
a[i][j]=++count;
}
for(j;j<s-1+pos;j++){
a[i][j]=++count;
}
for(i;i>=pos+1;–i){
a[i][j]=++count;
}
for(j;j>=1+pos;–j){
a[i][j]=++count;
}
/int i=pos,j=pos;
for(int k=0;k<s-1;k++){ //这种方法是每一层的行列的点个数都是固定的 改变的i,j的值
a[i++][j]=++count;
}
for(int k=0;k<s-1;k++){
a[i][j++]=++count;
}
for(int k=0;k<s-1;k++){
a[i–][j]=++count;
}
for(int k=0;k<s-1;k++){
a[i][j–]=++count;
}/
fun(pos+1,s-2); //s-2 是因为每向内进一层减少的上下和左右两边 pos是每一层开始的点
}
int main(){
fun(0,N);
print();
}