第二章：Statistical Modeling

本文参考翻译自：https://web.stanford.edu/class/bios221/book/Chap-Models.html

目录

2.2 The difference between statistical and probabilistic model

在第一章的点位的例子中，已知每个位置的误报率（假阳率false positives）为Bernoulli(0.01)，但被测患者数和确定的蛋白质长度是未知的。在这个例子中，我们假定有50个患者，每个患者在100个位置进行检测（假定是独立的），因此统计完50个病人，我们期望对于任意位置，50个患者中检测出多少个表位这个随机数服从参数为$50\times 0.01$=0.5的泊松分布。这就是我们的零假设。我们可以用数学推导的方法估计出100个位置观测到表位的最大值为7的概率约为$10^{-4}$，这是个很小的概率，然而在数据中观测到了，因此零假设很大概率是不可信的。
现在假设我们知道患者的数量和蛋白质的长度（这些由实验设计给出），但不知道分布律和假阳性率。一旦我们观测到数据，就需要从数据中估算概率模型（比如二项分布，正态分布，泊松分布），以及估计未知的模型参数。这就是本章所要讲的统计推断。

2.3 A simple example of statistical modeling

Start with the data
建模分为两个过程。首先我们需要一个合理的概率模型来对数据过程进行建模。类似我们在第一章中看到的，离散计数数据可以用简单的概率分布（二项分布，多项式分布或泊松分布）。正态分布或钟形曲线通常是连续数据的良好模型。分布也可以是这些最基本的分布的混合。
回顾第一章的表位的那个例子

load("../data/e100.RData")
e99 = e100[-which.max(e100)]

Goodness-of-fit : visual evaluation
我们第一步要从备选分布中求出拟合值；这需要从图形上和从数量上考察拟合优度。对于离散数据，我们绘制频率的条形图（barplot),对于连续变量，我们将查看直方图（histogram)。

barplot(table(e99), space = 0.8, col = "chartreuse4")

但是如果不进行比较，很难决定哪种理论分布更适合数据。一种可视化的拟合优度图称为“rootogram“（Cleveland 1988）。
根图（rootogram）将理论值的平方根显示为红点，而观测值的平方根显示为下拉矩阵。

library("vcd")
gf1 = goodfit( e99, "poisson")
rootogram(gf1, xlab = "", rect_gp = gpar(fill = "chartreuse4"))

如果观测值与理论值完全对应，则框的底部将与水平轴完全对齐。

例如：为了验证对比与一个真正服从参数为0.5的泊松分布，根图是否有差异。做模拟：

simp = rpois(100, lambda = 0.05)
gf2 = goodfit(simp, "poisson")
rootogram(gf2, xlab = "")

通过对比根图的表现，看上去用泊松分布模拟 e99数据很有道理。但别忘了，我们是先移除了outlier的。

Estimating the parameter of the Poisson distribution
泊松分布的均值取为多少的时候才使得数据看上去最有可能是那样的？首先我们来统计一下数据：

table(e100)

table(rpois(100, 3))

对比参数为3的泊松分布，看起来数据中有更多的2和3。所以e100数据不太可能是参数为3的泊松分布。

我们可以一直这样试下去，但我们还可以做得更好。下面我计算一下假如分布为参数为m的泊松分布，观察到该数据的概率有多大：

$P(58\times 0,34\times 1,7\times 2,one7|dataarePoisson(m))$
$=p(0{)}^{58}p(1{)}^{34}p(2{)}^{7}p(7)$
当m=3时，结果为：

prod(dpois(c(0, 1, 2, 7), lambda = 3) ^ (c(58, 34, 7, 1)))

得到的这个概率就是关于参数$\lambda$的似然函数(likelihood function of $\lambda$)，记作:
$L(\lambda ,x=(k_1,k_2,k_3,...))={\prod }_{i=1}^{n}f(k_i)$
比如对于泊松分布，$f(k)=e^{-\lambda }\frac{{\lambda }^k}{k!}$
下面我们通过编程来计算$\lambda$取值从0.05到0.95之间100个数时，对应的泊松分布的似然函数的值。

loglikelihood  =  function(lambda, data = e100) {
  sum(log(dpois(data, lambda)))
}

lambdas = seq(0.05, 0.95, length = 100)
loglik = vapply(lambdas, loglikelihood, numeric(1))
plot(lambdas, loglik, type = "l", col = "red", ylab = "", lwd = 2,
     xlab = expression(lambda))
m0 = mean(e100)
abline(v = m0, col = "blue", lwd = 2)
abline(h = loglikelihood(m0), col = "purple", lwd = 2)
m0

实际上在vcd包中，有个函数可以实现一行代码就计算出上述的所有运算。

gf  =  goodfit(e100, "poisson")
names(gf)

gf$par

结果是一样的。

2.3.1 Classical statistics for classical data

我们用数学推导得到在上面例子中$\lambda$的极大似然估计。
前面所讲的是统计推断的第一部分，从手头的数据中估计出分布的未知参数。统计中一个重要的内容是推断数据来自哪一类分布。这就是下面要讲到的内容。
在经典的统计假设框架下，我们为数据考虑一个单一的模型，称为“无效模型（null model)”。“无效模型（null model)”制定了一个“无趣”的基线，例如，所有观察值都来自相同的随机分布，而不管他们来自哪个组或接受的什么治疗。然后我们在这个假设下计算概率，检测是否有“有趣”的事情发生。通常，这就是我们所能做到的最好的事了，因为我们没有足够信息知道“有趣”的或备择模型应该是什么。而在有的时候，我们可以比较两个“竞争”模型，后文将讲到。

另一个有用的方向是回归。我们可能想知道连续的协变量（例如温度）如何影响基于计数的响应变量。你可能已经接触过回归分析，其中响应变量y通过方程y=ax+b+e取决于协变量x，并且残差服从正态分布。而计数数据，相同类型的回归模型是可能的，尽管残差的概率分布需要是非正态的。在那种情况下，我们使用广义线性回归。

2.4 Binomial distributions and maximum likelihood

二项分布有两个参数：n次独立重复的试验；每次试验事件A发生的概率p。

2.4.1 An example

抽取了120个男性数据，对蓝绿色盲进行编码，如果不是色盲，编码为0，否则为1。数据总结如下：
则p的估计量为：
与前面泊松分布的例子一样，如果我们可以计算出关于参数p的许多个不同的值对应的似然函数的值，那么我们就可以绘制出似然函数图并且查看它在哪里跌落的最大。

probs  =  seq(0, 0.3, by = 0.005)
likelihood = dbinom(sum(cb), prob = probs, size = length(cb))
plot(probs, likelihood, pch = 16, xlab = "probability of success",
       ylab = "likelihood", cex=0.6)
probs[which.max(likelihood)]

可以看到最大似然估计并不恰好=1/12。这是因为probs中不包含$1/12\approx 0.0833$这个值。所以我们取的是probs中与0.0833最接近的那个值。

Likelihood for the binomial distribution
举个例子，计算二项分布的似然函数的值，并得到参数的最大似然估计。
不妨设 n=300,观测到 y=40 次成功。
取对数为：

loglikelihood = function(theta, n = 300, k = 40) {
  115 + k * log(theta) + (n - k) * log(1 - theta)
}

thetas = seq(0, 1, by = 0.001)
plot(thetas, loglikelihood(thetas), xlab = expression(theta),
  ylab = expression(paste("log f(", theta, " | y)")),type = "l")

2.5 More boxes:multinomial data

2.5.1 DNA count modeling: base pairs

DNA有四个基本分子：A - 腺嘌呤, C - 胞嘧啶, G - 鸟嘌呤, T - 胸腺嘧啶。

2.5.2 Nucleotide bias

这一节在一个真实数例中给出了估计和模拟测试的例子。在staphsequence.ffn.txt中可以找到金黄色葡萄球菌细菌基因的一条DNA链中的数据，我们可以用Bioconductor 包中的 Biostrings读取。

library("Biostrings")
staph = readDNAStringSet("../data/staphsequence.ffn.txt", "fasta")
staph[1]
letterFrequency(staph[[1]], letters = "ACGT", OR = 0)

问题：测试第一个基因的核苷酸是否均匀的分布在四个核苷酸上。
由于它们不同的生理特性，进化选择可以作用于不同的核苷酸频率。因此，我们可以问，来自这一数据的前10个基因是否来自同一多项式分布。我们没有先验的参考，我们只想确定核苷酸是否在前10个基因以相同的概率出现。如果不是这样，这将为我们提供证据，改变这10个基因的选择压力（selective pressure）。

letterFrq = vapply(staph, letterFrequency, FUN.VALUE = numeric(4),
         letters = "ACGT", OR = 0)
colnames(letterFrq) = paste0("gene", seq(along = staph))
tab10 = letterFrq[, 1:10]
computeProportions = function(x) { x/sum(x) }
prop10 = apply(tab10, 2, computeProportions)
round(prop10, digits = 2)

p0 = rowMeans(prop10)
p0

假设p0是所有10个基因的多项式分布的概率，并使用Monte Carlo模拟来测试在此假设下观察到的字母频率与期望值之间的偏差是否在合理范围内。
我们通过对p0和每列核苷酸的计数做外积求计数的期望值。

cs = colSums(tab10)
cs

`

expectedtab10 = outer(p0, cs, FUN = "*")
round(expectedtab10)

现在我们可以用rmultinom创建随机表，该表是根据零假设生成的，即认为多项式的概率分布由p0给出。

randomtab10 = sapply(cs, function(s) { rmultinom(1, s, p0) } )
all(colSums(randomtab10) == cs)

现在我们将这个重复B=1000次，从每个表中计算得到测试统计量，并将它储存在向量 simulstat中。

stat = function(obsvd, exptd = 20 * pvec) {
   sum((obsvd - exptd)^2 / exptd)
}
B = 1000
simulstat = replicate(B, {
  randomtab10 = sapply(cs, function(s) { rmultinom(1, s, p0) })
  stat(randomtab10, expectedtab10)
})
S1 = stat(tab10, expectedtab10)
sum(simulstat >= S1)

hist(simulstat, col = "lavender", breaks = seq(0, 75, length.out=50))
abline(v = S1, col = "red")
abline(v = quantile(simulstat, probs = c(0.95, 0.99)),
       col = c("darkgreen", "blue"), lty = 2)

从直方图中看到，当零假设成立时，我们看到s1=70.1的概率很小。因此拒绝这十个基因来自同一个多项式分布的假定。

2.6 The ${\chi }^2$ distribution

simulstat统计量的理论分布为参数为30($=10\times (4-1)$）的${\chi }^2$分布，严格来说，simulstat统计量由${\chi }^2$分布近似，表中的计数越大，近似就越好。我们可以据此计算s1=70.1的概率。正如上面看到的那样，蒙特卡洛难以计算小概率：计算的粒度为1/B,因此我们无法估计任何小于该值的概率，实际上，估计的不确定性更大。因此如果有任何理论适用，那将很有用。我们可以用另一个可视化的拟合优度工具QQ图来检测理论值与观测值的匹配程度。当比较两个分布时，无论是来自两个样本的分布，还是分别来自理论上的分布，以及来自样本，只看直方图是不够的。QQ图是基于查看每个分布的分位数的方法。

• 2.6.1 Intermezzo: quantiles and the quantile-quantile plot
  在上一章中，我们将100个样本值排序：$x_{(1)},x_{(2)},...,x_{(100)}$,假如我们想要得到22百分位数，我们可以取任何介于第22个值与第23个值之间的任何数，即$x_{(22)}\le c_{0.22}\le x_{(23)}$。换句话说，$c_{0.22}$的定义如下：
  $$\frac{\#(x_i^{{}^{\prime }}s\le c_{0.22})}{n}=0.22$$

任务：
1）随机生成1000个${\chi }_{30}^2$分布的随机数，画出其50个bins的直方图，并与simulstat统计量的值进行比较。
2）计算 simulstat统计量的分位数，并将其与${\chi }_{30}^2$分布的分位数进行比较。

qs = ppoints(100)
quantile(simulstat, qs)
quantile(qchisq(qs, df = 30), qs)

现在我们知道了什么是分位数，我们可以继续分位数-分位数图了。我们绘制了在零假设成立下模拟得到的simulstat统计量的值的分位数，与理论零假设分布${\chi }_{30}^2$的分位数的关系。

qqplot(qchisq(ppoints(B), df = 30), simulstat, main = "",
  xlab = expression(chi[nu==30]^2), asp = 1, cex = 0.5, pch = 16)
abline(a = 0, b = 1, col = "red")

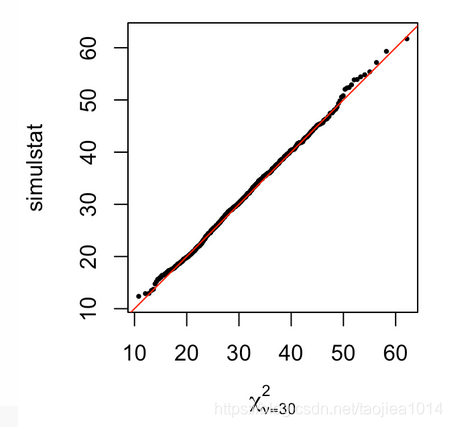在确信${\chi }_{30}^2$分布能够很好的描述simulstat统计量后，我们可以用它来计算p值。即在原假设下， pA=0.35, pC=0.15, pG=0.2, pT=0.3，我们观察到一个高达S1=70.1的值：

1 - pchisq(S1, df = 30)

p值这么小，原假设看上去不太可能为真。注意得到这个p值并不需要模拟1000次，并且计算显然快得多。

2.7 Chargaff’s Rule

Chargaff (Elson and Chargaff 1952)发现了核苷酸频率的重要模式。在利用分子的重量进行DNA测序之前很久，他猜测核苷酸是否以相同的概率出现。我们将此假设记为：$p_A=p_C=p_T=p_G$。

load("../data/ChargaffTable.RData")
ChargaffTable

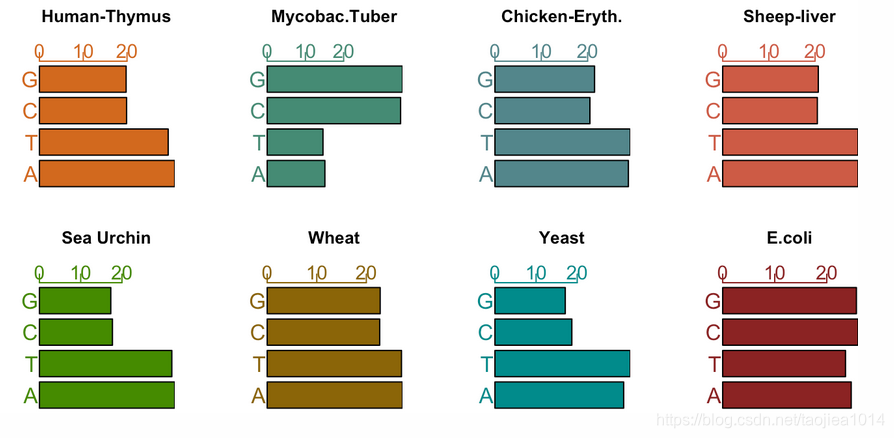问题：
这些数据看上去像是来自$p_A=p_C=p_T=p_G$的多项式分布吗？

Chargaff 提出了一种称为“碱基配对”的模式，该模式可确保生物体DNA中腺嘌呤（A）的量与胸腺嘧啶（T）的量完全匹配。同样的，鸟嘌呤（G）的量与胞嘧啶（C）的量匹配。这就是现在的“Chargaff’s rule”。
另一方面，生物体中C/G量与A/T量大不相同，跨生物体没有明显规律。根据Chargaff’s rule，我们可以通过汇总表的所有行提出一个统计量：
$$(p_A-p_T{)}^2+(p_C-p_G{)}^2,$$

我们会在数据之间比较，如果核苷酸是“可交换”的，将会发生什么。由于每行的概率没有特定的先后顺序，因为A与T的比例没有特殊关系，C与G之间的比例也没有特殊的关系。

statChf = function(x){
  sum((x[, "C"] - x[, "G"])^2 + (x[, "A"] - x[, "T"])^2)
}
chfstat = statChf(ChargaffTable)
permstat = replicate(100000, {
     permuted = t(apply(ChargaffTable, 1, sample))
     colnames(permuted) = colnames(ChargaffTable)
     statChf(permuted)
})
pChf = mean(permstat <= chfstat)
pChf

hist(permstat, breaks = 100, main = "", col = "lavender")
abline(v = chfstat, lwd = 2, col = "red")

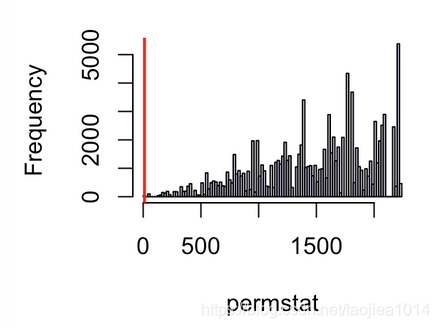从直方图看到，观测到11.1（红线标注即是）的概率很小，观测到小于等于11.1的概率为0.0014。因此数据有力的支持了Chargaff的看法。

2.7.1 Two categorical variables

到目前为止，我们已经探究了以下情况：数据取自：二项分布（是/否）和多项式分布(例如A,C,T,G或者其他诸如aa,aA,AA基因型。)然而我们可能在一组对象上测量两个（或多个）定性变量，比如眼睛颜色和头发颜色。于是我们可以得到列出所有眼睛颜色和头发颜色的交叉表，我们把这种表叫作列联表（contingency table）。列联表对许多生物数据(biological data types)都很有用。

HairEyeColor[,, "Female"]

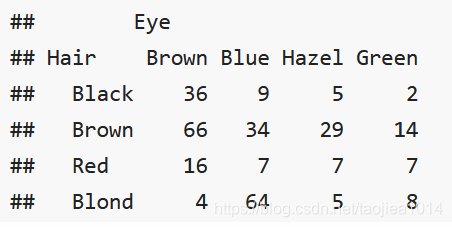查看数据的类型，维数。

str(HairEyeColor)

Color blindness and sex
由于缺少中等波长敏感视锥（绿色），Deuteranopia是一种色盲。患绿色盲的人（deuteranope ）只能分辨2至3种不同的色调，而正常的人可以看到7种不同的色调。通过对这类色盲的调查得到一张色盲和性别的关系的列联表。

load("../data/Deuteranopia.RData")
Deuteranopia

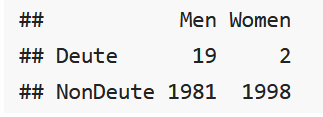我们如何测试性比与色盲之间是否存在关系？我们提出原假设：性别与色盲是互相独立的二项分布。在原假设成立的假定下，可以估计列联表中各个计数发生的概率，并将观察到的计数与期望计数比较。

chisq.test(Deuteranopia)

p值很小，因此我们应该期望在零假设: $p_A=p_T=p_C=p_G$下看到这样一个表的可能性很小。
我们将在10.3.2节看到针对此类数据的另一种测试，叫作Fisher’s exact test （也叫the hypergeometric test）。该测试被广泛用于测试一系列显著表达基因中某些基因类型的过度表达。

2.7.2 A special multinomial: Hardy-Weinberg equilibrium

在这里我们重点介绍了通过组合两个等位基因M、N得到的具有三个可能结果的多项式分布的用法。假设总体中等位基因M的频率为p，N的频率为1-p。如果基因型中两个等位基因的频率是独立的，即所谓的哈迪.温伯格平衡，哈迪.温伯格将研究p与q的关系。如果种群足够大，种群个体之间独立交配，没有突变，没有选择，没有迁移，没有遗传漂变，这种情况就会发生。这三种基因型的概率如下：
$$p_{MM}=p^2,p_{NN}=q^2,p_{MN}=2pq(2.6)$$

我们仅观察到基因型MM,NN,MN的频率$(n_{MM},n_{NN},n_{MN})$以及频数的总和$S=n_{MM}+n_{NN}+n_{MN}$,我们可以利用(2.6)式给定多项式分布的各可能结果的概率写出似然函数的表达式：
$$P(n_{MM},n_{NN},n_{MN}|p)=(\genfrac{}{}{0ex}{}{S}{n_{MM},n_{NN},n_{MN}})(p^2{)}^{n_{MM}}(2pq{)}^{n_{MN}}(q^2{)}^{n_{NN}}$$
以及在HWE下的loglik:
$$L(p)=n_{MM}log(p^2)+n_{MN}log(2pq)+n_{NN}log(q^2)$$
使得L§取得最大值的p值为：
$$p=\frac{n_{MM}+n_{MN}/2}{S}$$
给定参数$(n_{MM},n_{NN},n_{MN})$,似然函数$L(p)$只是p的函数。

library("HardyWeinberg")
data("Mourant")
Mourant[214:216,]

nMM = Mourant$MM[216]
nMN = Mourant$MN[216]
nNN = Mourant$NN[216]
loglik = function(p, q = 1 - p) {
  2 * nMM * log(p) + nMN * log(2*p*q) + 2 * nNN * log(q)
}
xv = seq(0.01, 0.99, by = 0.01)
yv = loglik(xv)
plot(x = xv, y = yv, type = "l", lwd = 2,
     xlab = "p", ylab = "log-likelihood")
imax = which.max(yv)
abline(v = xv[imax], h = yv[imax], lwd = 1.5, col = "blue")
abline(h = yv[imax], lwd = 1.5, col = "purple")

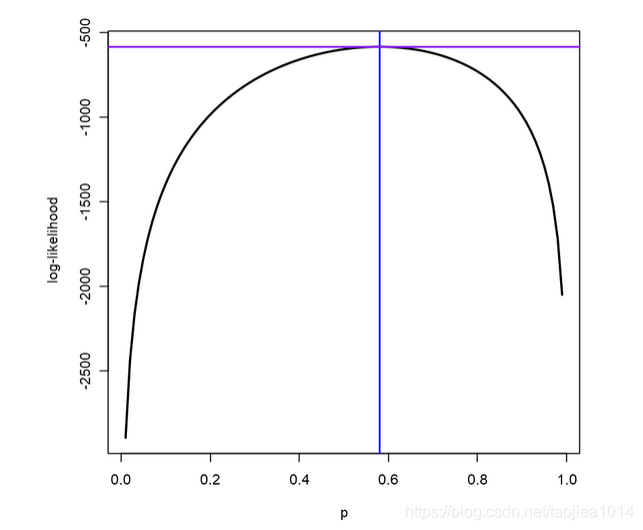我们可以用HardyWeinberg包中的af函数计算${\hat{p}}_{MM},{\hat{p}}_{MN},{\hat{p}}_{NN}$

phat  =  af(c(nMM, nMN, nNN))
phat

pMM   =  phat^2
qhat  =  1 - phat

在HardyWeinberg平衡条件下的期望值为：

pHW = c(MM = phat^2, MN = 2*phat*qhat, NN = qhat^2)
sum(c(nMM, nMN, nNN)) * pHW

我们可以将其与观测值进行比较，看到期望值与观测值非常接近。我们可以通过模拟或者${\chi }^2$检验进一步检测是否可以拒绝HardyWeinberg模型。de Finetti (Finetti 1926; Cannings and Edwards 1968)设计了一种对Hardy-Weinberg模型拟合优度的可视化评估方法。这种方法把每个样本当作一个图上的一个点，点的坐标由每个不同的等位基因的比例给出。
Visual comparison to the Hardy-Weinberg equilibrium
我们用HWTernaryPlot函数展示数据，并在图形上将其与 Hardy-Weinberg equilibrium进行比较。

pops = c(1, 69, 128, 148, 192)
genotypeFrequencies = as.matrix(Mourant[, c("MM", "MN", "NN")])
HWTernaryPlot(genotypeFrequencies[pops, ],
        markerlab = Mourant$Country[pops],
        alpha = 0.0001, curvecols = c("red", rep("purple", 4)),
        mcex = 0.75, vertex.cex = 1)

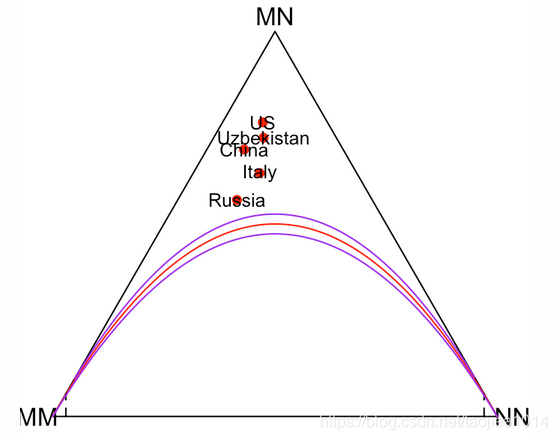这个de Finetti plot 表示把三种基因型的重心作为点。三角形每个角上的权重为各基因型的频率。红色曲线是Hardy-Weinberg模型，两条紫色线之间为接受域。从图上看上美国（US）远远不是HW平衡的。
按照上面的代码绘制ternary plot，然后向其添加其他数据点，你注意到了什么？你可以使用HWChisq函数支持你的讨论。

HWTernaryPlot(genotypeFrequencies[-pops, ], alpha = 0.0001,
   newframe = FALSE, cex = 0.5)

将总频率除以50，每种基因型保持相同的比例，并重新生成ternary plot，
图上的点看上去有什么不同?置信区间看上去发生了什么改变？为什么？

newgf = round(genotypeFrequencies / 50)
HWTernaryPlot(newgf[pops, ],
        markerlab = Mourant$Country[pops],
        alpha = 0.0001, curvecols = c("red", rep("purple", 4)),
        mcex = 0.75, vertex.cex = 1)

2.7.3 Concatenating several multinomials: sequence motifs and logos

所谓“ Kozak Motif”是在编码区的起始密码子ATG附近的序列。起始密码子本身具有固定的拼写，但在它左侧的位置5，有一种核苷酸模式，其字母远不是等可能出现的。
我们通过给出位置权重矩阵（PWM）或给出每个位置的多项式分布概率的特定位置得分矩阵（PSSM），来总结这一点。

library("seqLogo")
load("../data/kozak.RData")
kozak

pwm = makePWM(kozak)
seqLogo(pwm, ic.scale = FALSE)

这个图叫作sequence logo，是用与位置有关的多项式分布对Kozak motif建模。它在对数刻度上编码每个位置的变化量。字母越大，表示在这个位置出现该核苷酸的概率越大。

如果我们有多个分类变量，我们已经看到它们很少是独立的（头发与眼睛的颜色、性别与色盲）。我们将在第九章看到可以用列联表的多元分解来探索这些依赖关系的模式。在这里，我们将研究分类变量相关关系的一种特定的重要的情形：在分类变量的序列（或链上）（例如随着时间推移或沿着生物聚合物）所产生的依赖。

2.8 Modeling sequential dependencies: Markov chains

如果我们要预测明天的天气，可以合理的猜测，它很可能与今天的天气相同，除此之外，我们还可以陈述各种可能的变化的概率。同样的推理也可以反过来用：我们可以用今天的天气来“预测”昨天的天气。这是马尔可夫假设的一个示例：对明天的预测仅取决于昨天事物的状态，而不取决于前天或三周前（我们可能使用的所有信息都包含在今天的天气中）。这样的假设不一定完全正确，但应该足够好。直观的，我们可以把这个假设推广到前k天（k是个有限的数字，不是太大）。马尔可夫假设的本质是过程具有有限的“记忆”，因此预测只需要回顾有限的时间。
除了用于时间序列，我们还可以将其用于生物学序列。在DNA中，我们可以看到特定的模式顺序，因此成对的核苷酸（称为grams),例如CG, CA, CC 和 CT出现的频率并不相同。例如在基因组的某些部分，我们看到CA的频率比在独立条件下的预期频数要多。
$$p(CA)\ne p(C)p(A)$$
我们把序列中此种依赖关系建模为马尔科夫链：
$$p(CA)=p(NCA)=p(NNCA)=p(...CA)=p(A|C)$$
其中N代表任何核苷酸。p(A|C)表示链条前面位置的碱基是C，当前位置为A的概率。

有4个状态的马尔科夫链图。

2.9 Bayesian Thinking

到目前为止，我们使用的都是古典的“频数”派方法。这种方法在估计已知分布的未知参数的时候，把待估的参数当作固定的数字。然而这种方法没有考虑可能我们用来估计参数的数据中也包含了的一些关于该参数的信息。我们需要一种方法，将参数看作是随机的，能够利用手头的数据更新随机参数的信息。
Haplotypes
为了尽量避免使用数学公式，我们从一个例子开始。单倍体是等位基因的集合（DNA序列变异体），这些等位基因在染色体上是相邻的，通常一起遗传（重组往往不会使他们断开连接），因此具有遗传联系。在这种情况，我们研究Y染色体上的连锁变体。
首先我们回顾一下研究单倍体频数分析背后的动机，之后回顾一下似然的想法。然后我们将说明如何将未知参数当作随机变量，并用先验分布对他们的不确定性建模。然后我们将看到如何将观测的新数据合并到概率分布中，并用来计算相关参数的后验置信区间。

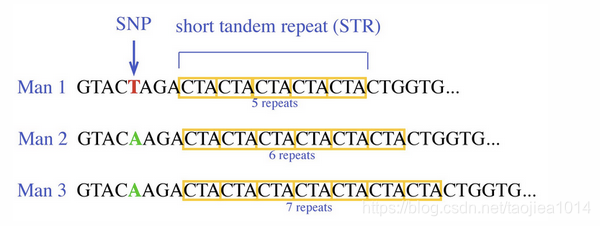当重复两个或多个核苷酸的模式并且重复的序列彼此相邻时，DNA中会发生短串联重复序列（STR）。短串联重复序列也称为微卫星（microsatellite）。模式的长度范围在2到13个核苷酸，并且重复的数目在不同个体之间可以高度不同。STR numbers可以用作遗传特征，称为单倍体。

2.9.1 Example: haplotype frequencies

我们想要估计由一组不同的短串联重复序列（STR）组成的特定Y单倍体序列的比例。用于DNA取证的特定STR位置的STR numbers组合由特定位置的重复数标记。可以在http://www.usystrdatabase.org访问美国的Y染色体STR数据库。以下是STR单倍型表的简短摘录：

haplo6=read.table("../data/haplotype6.txt",header = TRUE)
haplo6

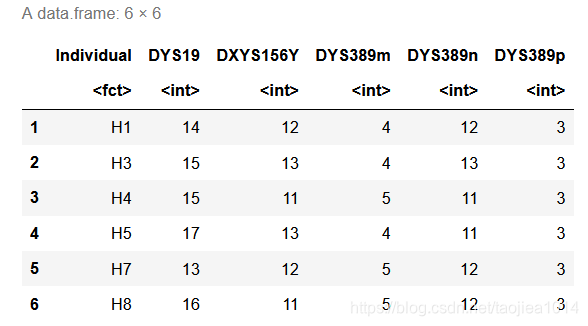这表示单倍体H1在位置DYS19重复了14次，在位置DXYS156Y重复了12次$....$同一父系血统的男性之间共享通过使用这些 Y-STR谱图创建的单倍体。因此，两个不同的人可能共享相同的谱图。我们需要找到感兴趣的群体中感兴趣的单倍体的潜在比例。我们把收集到的数据中出现单倍体视为二项分布中的“成功”。

2.9.2 Simulation study of the Bayesian paradigm for the binomial

贝叶斯观点认为待估参数不是一个未知的固定的数字，而是一个服从某分布的随机数。原则上，我们可以使用任何我们认为参数可能服从的分布，不过当我们查看一个表示比例或者概率的参数，且其取值介于0和1之间，beta分布通常是一个方便的选择。它的分布密度函数如下：

beta分布的均值为$\frac{\alpha }{\alpha +\beta }$。从密度图可以看到，beta分布依赖于其参数，参数取值不同，密度图的形态也不同。因而beta分布作为一个“复杂”的分布，可以适用于很多情况。beta分布同时也具有很好的数学性质：如果我们认为参数$\theta$的先验分布是某个beata分布，观测一个n次二项分布试验的数据集，则尽管使用了更新的参数，$\theta$的后验分布也是beta分布。我们不打算在这进行数学证明，但是下面用模拟来验证。
The distribution of Y
如果参数$\theta$是个随机数，那么Y的分布是什么呢？我们把这个Y的分布称为Y的边际分布，让我们对其进行模拟。首先我们生成10，000个随机数$\theta$，对每个$\theta$，然后生成相应的Y。

rtheta = rbeta(100000, 50, 350)
y = vapply(rtheta, function(th) {
  rbinom(1, prob = th, size = 300)
}, numeric(1))
hist(y, breaks = 50, col = "orange", main = "", xlab = "")

上面生成Y的过程也可以通过使用R的向量化功能用一行代码实现：

rbinom(length(rtheta), rtheta, size = 300)

Histogram of all the thetas such that Y=40: the posterior distribution

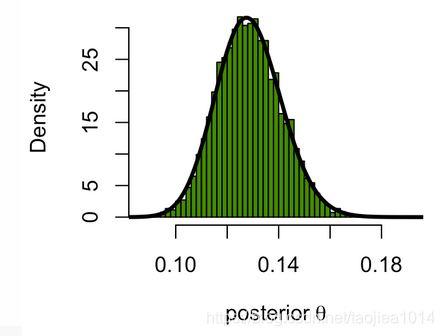在假设Y=40的情况下，得到$\theta$的后验分布。绿色的直方图是模拟得到的$\theta$的后验分布，曲线是理论的$\theta$的分布。

thetaPostEmp = rtheta[ y == 40 ]
hist(thetaPostEmp, breaks = 40, col = "chartreuse4", main = "",
  probability = TRUE, xlab = expression("posterior"~theta))
densPostTheory  =  dbeta(thetas, 90, 610)
lines(thetas, densPostTheory, type="l", lwd = 3)

我们还可以检验模拟的分布和理论分布的均值，看它们是否很接近：

mean(thetaPostEmp)
dtheta = thetas[2]-thetas[1]
sum(thetas * densPostTheory * dtheta)

为了得到理论分布densPostTheory的均值的近似值，我们使用数值积分计算${\int }_0^1\theta f(\theta )d\theta$,这在高维的时候常是不可行的。比如在图像分析中，常遇到参数是高维的。而蒙特卡洛积分可以计算参数是高维的情形的积分。

thetaPostMC = rbeta(n = 1e6, 90, 610)
mean(thetaPostMC)

我们可以用QQ图来检验蒙特卡洛样本thetaPostMC与thetaPostEmp之间的一致性。

qqplot(thetaPostMC, thetaPostEmp, type = "l", asp = 1)
abline(a = 0, b = 1, col = "blue")

Posterior distribution is also a beta
现在我们看到后验分布也是beta分布。我们通过分别将先验参数$\alpha =50$，$\beta =350$加到y=40和n-y=260上去。得到后验分布为：$$beta(90,610)=beta(\alpha +y,\beta +n-y)$$.
我们可以用后验分布得到参数的最佳估计，这称为MAP估计，在这个例子中最优估计为$\theta =\frac{\alpha -1}{\alpha +\beta -2}$。
Suppose we had a second series of data
在我们观测到前面的数据后，得到了新的先验分布beta(90,610)，假如现在我们又搜集到了一组新的观测，n=150 ，y=25 次成功, n-y=125 次失败。则现在参数$\theta$的最优估计MAP是什么？
与前面的推理类似，新的后验分布为beta(90+25,610+125)=beta(115,735),这个分布的均值为$\frac{115}{850}\approx 0.135$,因此$\theta$的估计可以为0.135。
理论的MAP为beta(115,735)的众数，也就是$\frac{114}{848}\approx 0.134$。下面我们用数值的方法验证：

densPost2 = dbeta(thetas, 115, 735)
mcPost2   = rbeta(1e6, 115, 735)
sum(thetas * densPost2 * dtheta)  # mean, by numeric integration

mean(mcPost2)                     # mean, by MC

thetas[which.max(densPost2)]      # MAP estimate

Confidence Statements for the proportion parameter
现在我们要对由数据给出的比例给出总结报告，一个常用的方法是给出后验置信区间，置信区间的贝叶斯版本。我们可以给出后验分布的2.5%与97.5%分位数。

quantile(mcPost2, c(0.025, 0.975))

2.10 Example: occurrence of a nucleotide pattern in a genome

到目前为止，我们看到的例子都是关于离散计数数据或者分类数据的，让我们看一个准连续的关于距离的分布的例子。对基因组序列序列中特定的motif之间的距离的分布进行的案例分析也有助于我们探索Bioconductor特定基因组序列操作。
R软件中Biostrings包提供了处理序列数据的工具。R中已有的基本数据结构或类有DNAString与 DNAStringSet。这些使我们能够有效的处理一个或多个DNA序列。Biostrings包中还包含代表其他氨基酸和一般字符串的其他类别。

library("Biostrings")

下面我们通过tutorial vignette，探索Biostrings包中所提供的一些有用的数据和基本的功能。

vignette(package = "Biostrings")
vignette("BiostringsQuickOverview", package = "Biostrings")

BSgenome 包提供对许多基因组的访问，您可以通过键入以下代码来访问包含整个基因组序列的数据包的名称。

library("BSgenome")
ag = available.genomes()
length(ag)

ag[1:2]

我们将探索在大肠杆菌的基因组中AGGAGGT motif的出现。 这是有助于启动细菌中的蛋白质合成的Shine-Dalgarno motif。我们使用一种特殊的菌株，大肠杆菌Escherichia coli str. K12 substr.DH10B，它是实验室中常用的菌株，其NCBI登录号为NC_010473。

library("BSgenome.Ecoli.NCBI.20080805")
Ecoli
shineDalgarno = "AGGAGGT"
ecoli = Ecoli$NC_010473

我们可以使用countPattern函数在宽度为50，000的窗口计算the pattern出现的次数。

window = 50000
starts = seq(1, length(ecoli) - window, by = window)
ends   = starts + window - 1
numMatches = vapply(seq_along(starts), function(i) {
  countPattern(shineDalgarno, ecoli[starts[i]:ends[i]],
               max.mismatch = 0)
  }, numeric(1))
table(numMatches)

这个表看上去服从什么分布？泊松分布是个好的选择。

library("vcd")
gf = goodfit(numMatches, "poisson")
summary(gf)

distplot(numMatches, type = "poisson")

我们用matchPattern函数检查匹配项。

sdMatches = matchPattern(shineDalgarno, ecoli, max.mismatch = 0)

你可以在R命令行中键入sdMatches以获得该对象的摘要。它包含65个模式匹配的位置，表示为原始序列上的一组所谓视图，它们的距离是多少？

betweenmotifs = gaps(sdMatches)

我们找到模型描述the gap sizes between motifs的分布。如果 the motifs在随机的位置发生，则我们期望the gap lengths服从指数分布。为什么我们猜是指数分布呢？当数据是沿着序列上的独立的，伯努利的事件，则the gap lengths是指数分布的。你可能熟悉放射性衰变，其中放射之间的等待时间服从指数分布。
下面的代码评估了这个假设。如果指数分布很适合，则所有的点应大致位于一条直线上。

library("Renext")
expplot(width(betweenmotifs), rate = 1/mean(width(betweenmotifs)),
        labels = "fit")

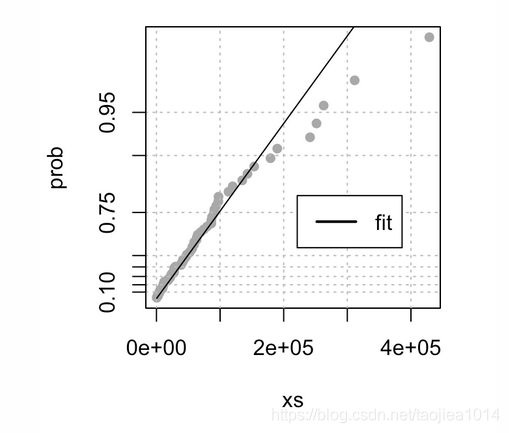分布的右尾处有些偏离，可能是什么原因造成的？

2.10.1 Modeling in the case of dependencies

正如我们在2.8节看到的，核苷酸通常是互相依赖的：在给定位置看到某核苷酸的可能性往往取决于它周围的核苷酸。在这里我们将使用马尔科夫链模拟这种依赖关系。我们将研究人类基因组8号染色体的区域，并尝试发现CpG区域与其他区域的差异。CpG代表 5’-C-phosphate-G-3’;这意味着C沿链通过磷酸酯与G相连（这与2.7节的C-G碱基配对无关）。CpG二核苷酸中的胞嘧啶可以被甲基化，从而改变基因表达的水平。这种类型的基因调控是表观遗传学的一部分。
我们使用数据（generated by Irizarry, Wu, and Feinberg (2009)），告诉我们这些 islands中的起点和终点在在基因组中的位置，并查看核苷酸和二元图"CG"，"CT“，‘CA’, ‘CC’的频率。于是我们可以问在nucleotide occurrences之间是否存在依赖关系，如果存在，如何建模。

library("BSgenome.Hsapiens.UCSC.hg19")
chr8  =  Hsapiens$chr8
CpGtab = read.table("../data/model-based-cpg-islands-hg19.txt",
                    header = TRUE)
nrow(CpGtab)
head(CpGtab)

irCpG = with(dplyr::filter(CpGtab, chr == "chr8"),
         IRanges(start = start, end = end))

在上面的代码中，我们仅从CpGtab中提取包含八号染色体的子集，然后创建一个IRanges 对象，这个IRanges 对象的的开始和结束位置由CpGtab的同名列定义。IRanges是用于数学间隔的通用容器。

grCpG = GRanges(ranges = irCpG, seqnames = "chr8", strand = "+")
genome(grCpG) = "hg19"

我们创建了生物学环境。下面进行可视化。

library("Gviz")
ideo = IdeogramTrack(genome = "hg19", chromosome = "chr8")
plotTracks(
  list(GenomeAxisTrack(),
    AnnotationTrack(grCpG, name = "CpG"), ideo),
    from = 2200000, to = 5800000,
    shape = "box", fill = "#006400", stacking = "dense")

现在，我们在the CpG islands相对应的染色体序列定义了 views，记为irCpG，以及irCpG之间的区域的views。生成的CGIview 和 NonCGIview仅包含坐标，并不包含序列本身（它们在大对象Hsapiens$chr8中）

CGIview    = Views(unmasked(Hsapiens$chr8), irCpG)
NonCGIview = Views(unmasked(Hsapiens$chr8), gaps(irCpG))

我们使用这些数据计算CpG islands与non-islands之间的转移计数。

seqCGI      = as(CGIview, "DNAStringSet")
seqNonCGI   = as(NonCGIview, "DNAStringSet")
dinucCpG    = sapply(seqCGI, dinucleotideFrequency)
dinucNonCpG = sapply(seqNonCGI, dinucleotideFrequency)
dinucNonCpG[, 1]

NonICounts = rowSums(dinucNonCpG)
IslCounts  = rowSums(dinucCpG)

对于4状态马尔科夫链，我们将转移矩阵定义为行表示起始状态，列表示终止状态。

TI  = matrix( IslCounts, ncol = 4, byrow = TRUE)
TnI = matrix(NonICounts, ncol = 4, byrow = TRUE)
dimnames(TI) = dimnames(TnI) =
  list(c("A", "C", "G", "T"), c("A", "C", "G", "T"))

MI = TI /rowSums(TI)
MI

MN = TnI / rowSums(TnI)
MN

各行的转移概率是不同的，例如在the islands (MI)的转移矩阵中，从C转移到A的转移概率为0.201，而从T到A的转移概率为0.098。
与其他地方相比，CpG islands中不同的核苷酸的相对频率是否不同？

freqIsl = alphabetFrequency(seqCGI, baseOnly = TRUE, collapse = TRUE)[1:4]
freqIsl / sum(freqIsl)

freqNon = alphabetFrequency(seqNonCGI, baseOnly = TRUE, collapse = TRUE)[1:4]
freqNon / sum(freqNon)

这显示了一种相反的模式：在the CpG islands中，C和G的频率约为0.32，而在non-CpG islands中，A和T的频率约为0.30。
我们如何利用这些差异决定给定序列是否来自CpG island？
利用${\chi }^2$分布比较观测的频数与freqIsl频数，以及观测频数与 freqNon频数。对于较短序列，这可能不够灵敏。下面给出更灵敏的方法。
给定一个序列，我们不知道它是否来自 CpG island，我们想知道它属于 CpG island与它属于其他的概率之比。我们基于所谓的优势比（odds ratio）来计算得分。举个例子：假设x是序列ACGTTATACTACG，我们想知道它是否来自CpG island。
如果我们用一阶的马尔科夫链对序列建模，假设该序列来自CpG island，则我们可以写：
$$P_i(x=ACGTTATACTACG)=P_i(A)P_i(AC)P_i(CG)P_i(GT)P_i(TT)\times P_i(TA)P_i(AT)P_i(TA)P_i(AC)P_i(CG)$$
$$\text{\hspace{1em}(2.7)}$$
我们将把这个概率与x序列属于non-islands的概率进行比较。正如我们在上面看到的，这些概率趋于不同。我们取它们的比值，看它们的比值是大于1还是小于1。这些概率是许多小概率的乘积，因此会非常的小。我们用取对数解决这个问题。
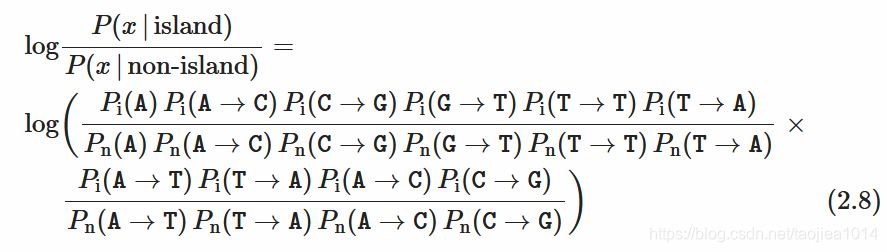这是对数似然比得分。为了提高计算速度，我们计算对数比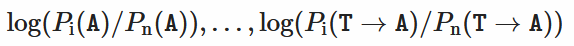然后把它们加起来就得到了所要的得分。

alpha = log((freqIsl/sum(freqIsl)) / (freqNon/sum(freqNon)))
beta  = log(MI / MN)

x = "ACGTTATACTACG"
scorefun = function(x) {
  s = unlist(strsplit(x, ""))
  score = alpha[s[1]]
  if (length(s) >= 2)
    for (j in 2:length(s))
      score = score + beta[s[j-1], s[j]]
  score
}
scorefun(x)

下面的代码中我们从seqCGI object中的2855个序列选择长度len = 100的序列，然后从the seqNonCGI object（每个序列都是DNAStringSet）的2854个序列中选。

generateRandomScores = function(s, len = 100, B = 1000) {
  alphFreq = alphabetFrequency(s)
  isGoodSeq = rowSums(alphFreq[, 5:ncol(alphFreq)]) == 0
  s = s[isGoodSeq]
  slen = sapply(s, length)
  prob = pmax(slen - len, 0)
  prob = prob / sum(prob)
  idx  = sample(length(s), B, replace = TRUE, prob = prob)
  ssmp = s[idx]
  start = sapply(ssmp, function(x) sample(length(x) - len, 1))
  scores = sapply(seq_len(B), function(i)
    scorefun(as.character(ssmp[[i]][start[i]+(1:len)]))
  )
  scores / len
}
scoresCGI    = generateRandomScores(seqCGI)
scoresNonCGI = generateRandomScores(seqNonCGI)

br = seq(-0.6, 0.8, length.out = 50)
h1 = hist(scoresCGI,    breaks = br, plot = FALSE)
h2 = hist(scoresNonCGI, breaks = br, plot = FALSE)
plot(h1, col = rgb(0, 0, 1, 1/4), xlim = c(-0.5, 0.5), ylim=c(0,120))
plot(h2, col = rgb(1, 0, 0, 1/4), add = TRUE)

在上面代码的前三行，我们删除了除了ACTG字母以外的其他字母。

2.11 Summary of this chapter

2.12 Further reading

2.13 Exercises

► Exercise 2.1

Generate 1,000 random 0/1 variables that model mutations occurring along a 1,000 long gene sequence. These occur independently at a rate of $10^{-4}$ each. Then sum the 1,000 positions to count how many mutations in sequences of length 1,000.

Find the correct distribution for these mutation sums using a goodness of fit test and make a plot to visualize the quality of the fit.
[1]: https://web.stanford.edu/class/bios221/book/Chap-Models.html