弱大数定理、强大数定理

最新推荐文章于 2025-02-28 23:47:00 发布

相逢一醉为前缘

最新推荐文章于 2025-02-28 23:47:00 发布

阅读量4.4k

点赞数 2

CC 4.0 BY-SA版权

分类专栏： R 文章标签：概率论

原文链接：https://www.ireader.com.cn/index.php?ca=Chapter.Index&pca=Chapter.Index&bid=12326569&cid=8

R 专栏收录该内容

35 篇文章

订阅专栏

马尔可夫不等式
切比雪夫不等式
弱大数定理
强大数定理

马尔可夫不等式

证明：对于 $a\geq 0$ ，令

$I=\left\{\begin{matrix} 1,x\geq a\\ 0,else \end{matrix}\right.$

由于 $X\geqslant 0$ ，所以恒有

$I\leqslant \frac{X}{a}$

两边同求期望，

$E(I)\leqslant E(\frac{X}{a})$ ,即为

$P(X\geqslant a)\leqslant \frac{E(X)}{a}$

作为推论，有切比雪夫定理：

证明：略

注：马尔可夫不等式和切比雪夫不等式的重要性在于：在只知道随机变量的期望（马尔科夫不等式）或者期望、方差都已知（切比雪夫不等式），可以导出概率的上界。

当然如果概率分布已知，可以直接算出概率的值而无需计算概率的上界。所以切比雪夫不等式的用途更多的是证明理论结果，更重要的是它可以被用来证明大数定理

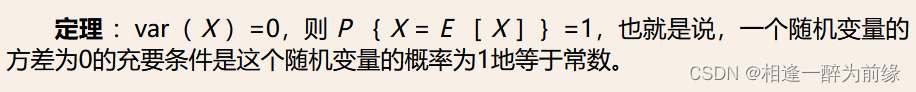
证明：利用切比雪夫不等式，对任何 $n\geq 1$

$P(|X-\mu |>\frac{1}{n})\leqslant \frac{D(X)}{\frac{1}{n^{2}}}=0$

令 $n\rightarrow \infty$ ，得

$0=\lim_{n\rightarrow \infty }P(|X-\mu |>\frac{1}{n})= P(\lim_{n\rightarrow \infty }[|X-\mu |>\frac{1}{n}])=P(X\neq \mu )$

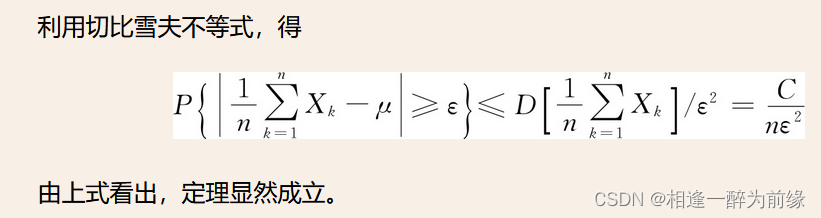
依概率收敛：

依概率收敛的性质：

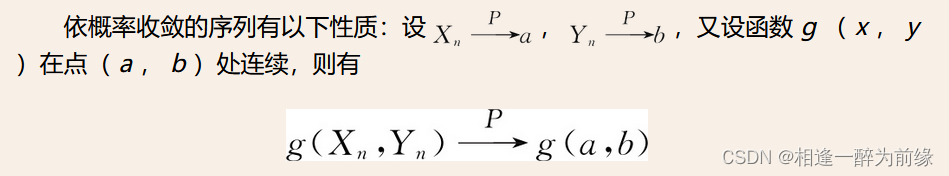
于是弱大数定理又可以表述为;

弱大数定理一开始是由雅各布.伯努利证明的，而且他所证明的其实是大数定理的一种特殊情况，其中 $X_{i}$ 只取1或0，即X为伯努利随机变量。他对定理的陈述和证明收录在1713年出版的巨著《猜度术》一书中。而切比雪夫是在伯努利逝世一百多年后才出生的，换言之，在伯努利的时代，切比雪夫不等式还不为人所知。上述弱大数定理是独立同分布序列的大数定理的最一般形式，它是由苏联数学家辛钦(Khinchin)所证明的。

与弱大数定理相对，还有强大数定理。强大数定理是概率论中最著名的结果。它表明，独立同分布的随机变量序列，前n个观察值的平均值以概率1的收敛为分布的期望值。

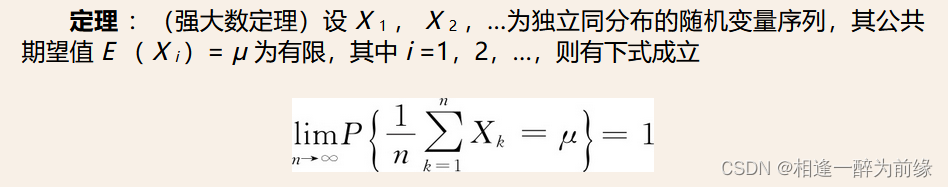
法国数学家博雷尔(Borel）最早在伯努利随机变量的特殊情况下给出了强大数定理的证明。而上述这个一般情况下的证明由苏联数学家柯尔莫哥洛夫(Kolmogorov)证明。

我们有必要分析一下强弱大数定理的区别。

参考:《统计学理论与方法——R语言版》

评论

被折叠的条评论为什么被折叠?

到【灌水乐园】发言

查看更多评论

添加红包

成就一亿技术人!

hope_wisdom

发出的红包

实付元

使用余额支付

点击重新获取

扫码支付

钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。