C语言经典题目--汉诺塔问题(小白必会)

---

问题简介：

汉诺塔问题的背景源自一个传说，讲述的是在一座印度寺庙中，有一座塔由三个柱子组成，其中一个柱子上摞着大小不同的圆盘。目标是将这些圆盘按照规定的规则从一个柱子移动到另一个柱子，规则包括每次只能移动一个圆盘，且不能将较大的圆盘放在较小的圆盘上面。

问题分析与求解思路：

我们先从阶数较少的情况进行分析，再通过归纳的方法得出最后的规律。

1.当汉诺塔阶数为1时，此时只需要一步完成。

2.当汉诺塔阶数为2时，则需要先将最小的放到中间柱子上，再将底座放到第三个柱子上上，最后再将最小的放到第三个柱子上，此时一共需要三步。

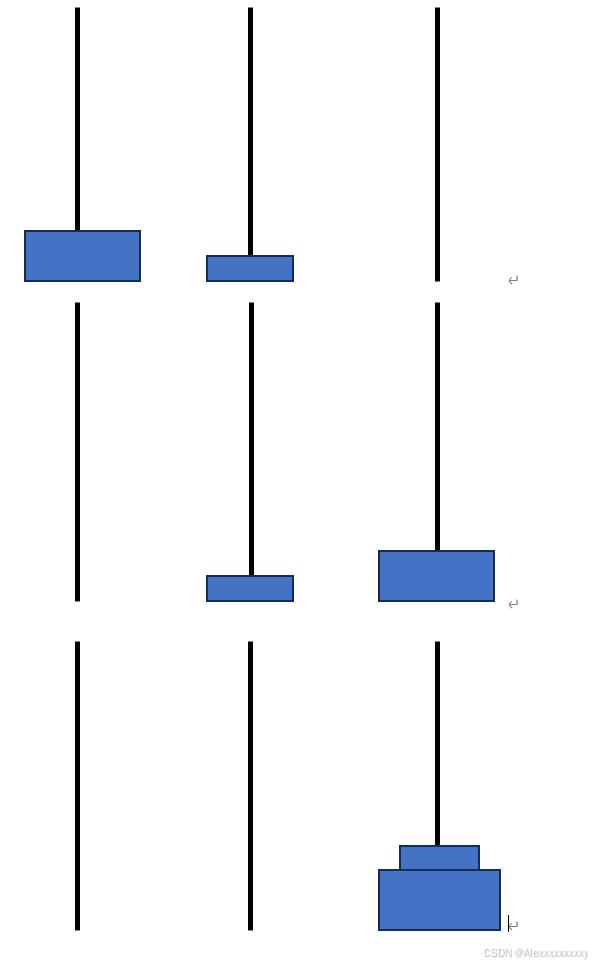
3.当汉诺塔的阶数为3时，我们通过试验可知，最少需要七步，具体步骤如下。

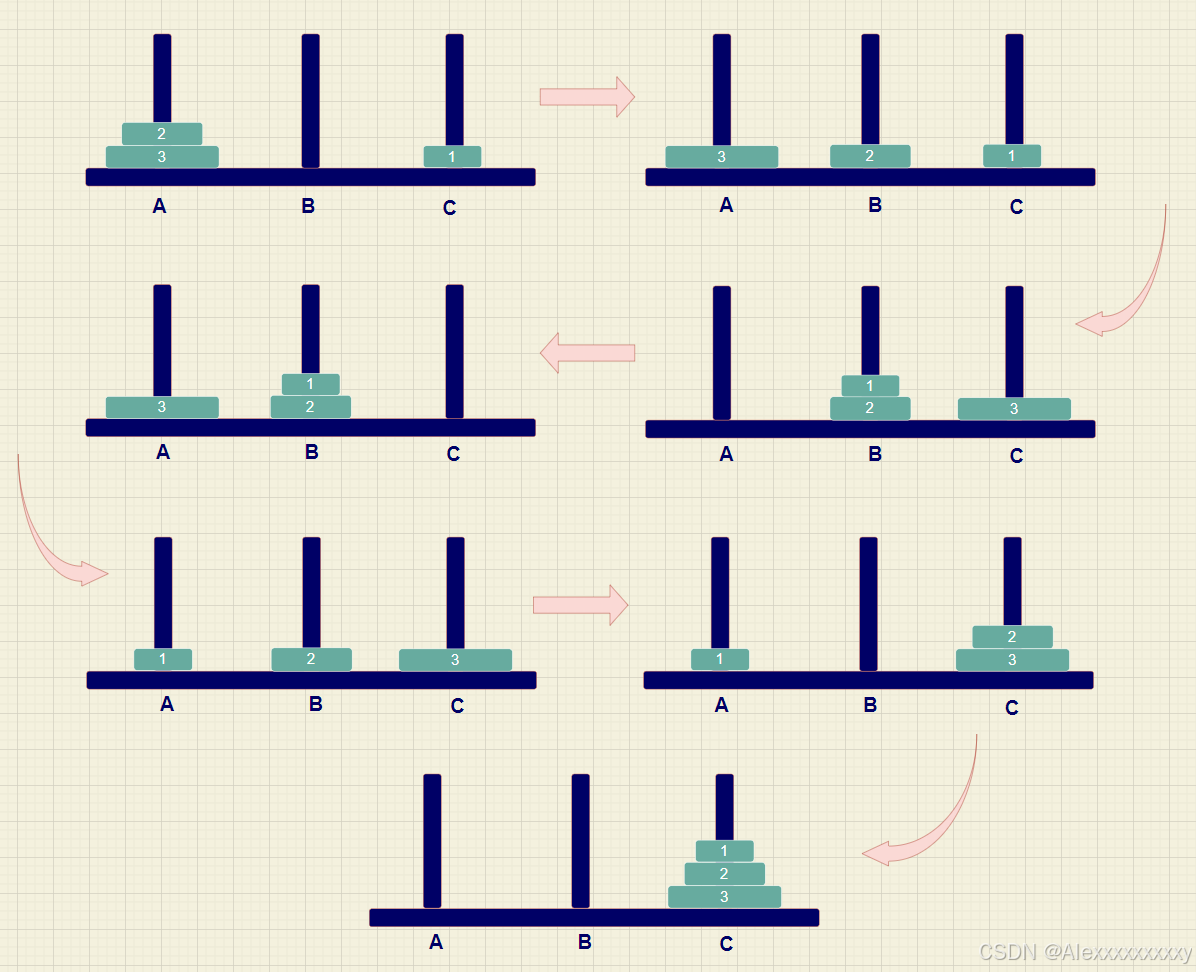
上图看起来步骤很多，很复杂，但是我们不妨换一种思考方式。

我们可以将上面的七步分成下列三个大步：(1)先将上面两个圆盘放在中间柱子上；(2)将底盘放到第三个柱子上；(3)将中间两个圆盘放到第三个柱子上。示意图如下。

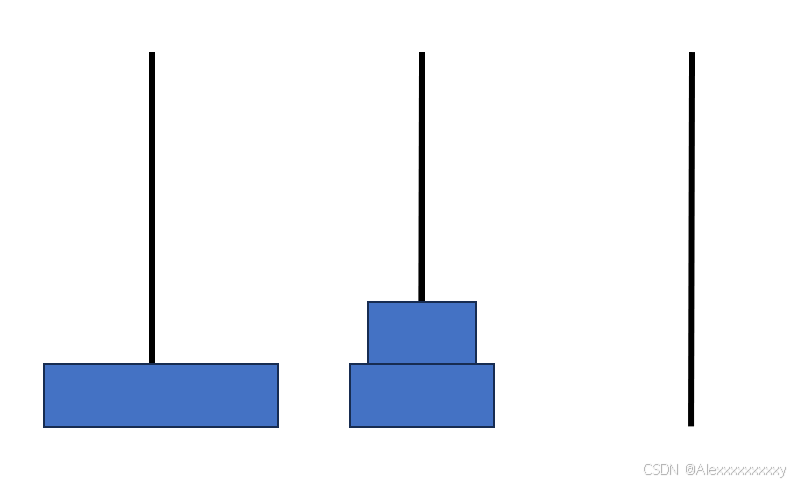
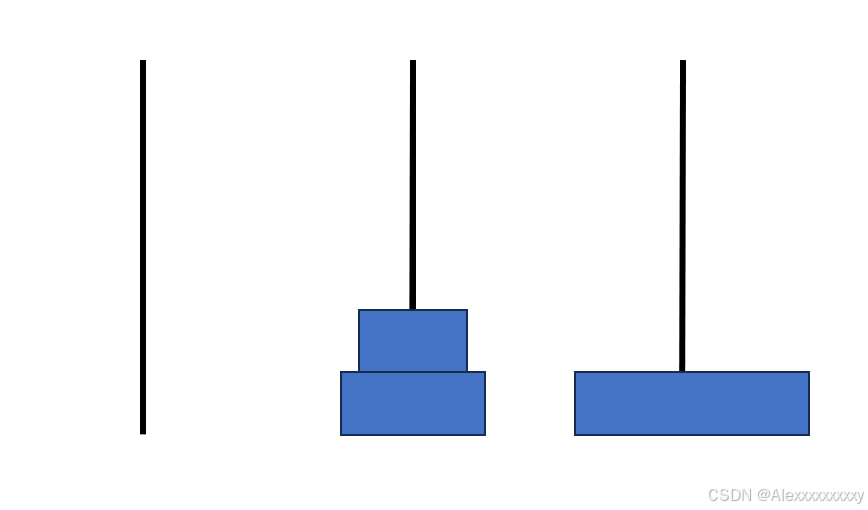
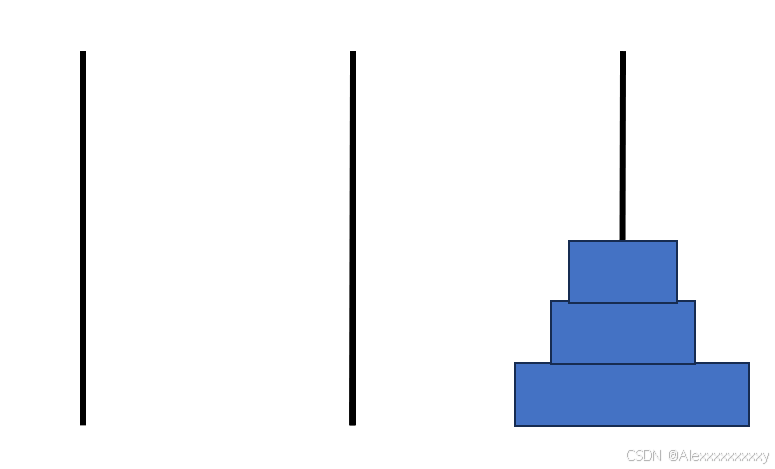
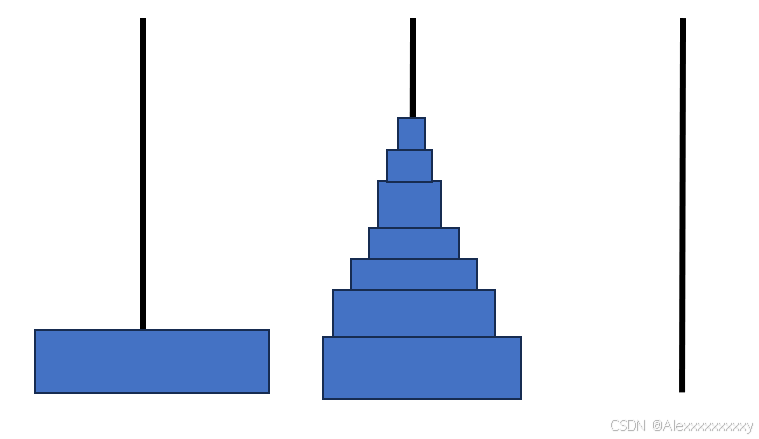
而第一步和第三步我们又可以看成一个2阶的汉诺塔问题，以此类推，对于一个n阶的汉诺塔问题，我们也可以分解成三步：(1)先将上面n-1个圆盘移动到中间的柱子上；(2)将底盘移动到第三个柱子上；(3)将中间的n-1个圆盘移动到第三个柱子上。而第一步和第三步又可以看成是一个n-1阶的汉诺塔问题。示意图如下。

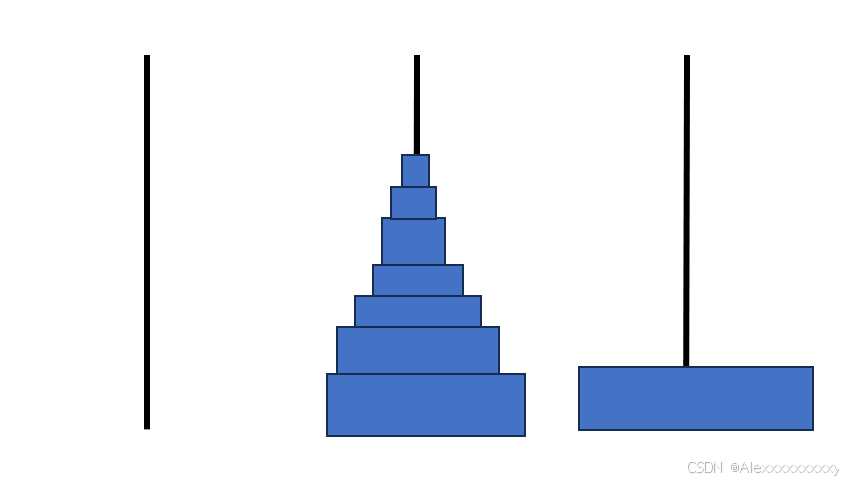
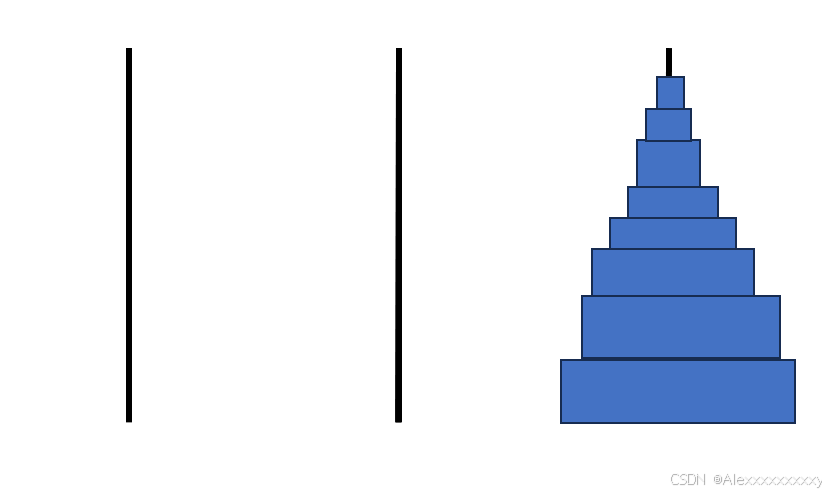
到这里我们可以看出汉诺塔的问题其实本质上就是一个递归问题，其思路和青蛙跳台阶的问题大致相同。

符号说明：

我们假设n阶汉诺塔问题所需最小的步骤为S(n)。

问题求解：

由上文我们可知，n阶汉诺塔问题与n-1阶汉诺塔问题有关联，其中第一步和第三步可以转化成n-1阶汉诺塔问题，于是我们可以得到关系式：S(n)=S(n-1)+1+S(n-1)。

所以我们直接用函数递归来解决。

#define _CRT_SECURE_NO_WARNINGS
#include <stdio.h>
int steps(int n)
{
	if (n == 1)
		return 1;
	else if (n == 2)
		return 3;
	else
		return steps(n - 1) + 1+steps(n-1);
}
int main()
{
	int n = 0;
	int step = 0;
	printf("请输入汉诺塔的阶数>:");
	scanf("%d", &n);
	step = steps(n);
	printf("\n共需要%d步",step);
	return 0;
}

结果如下：

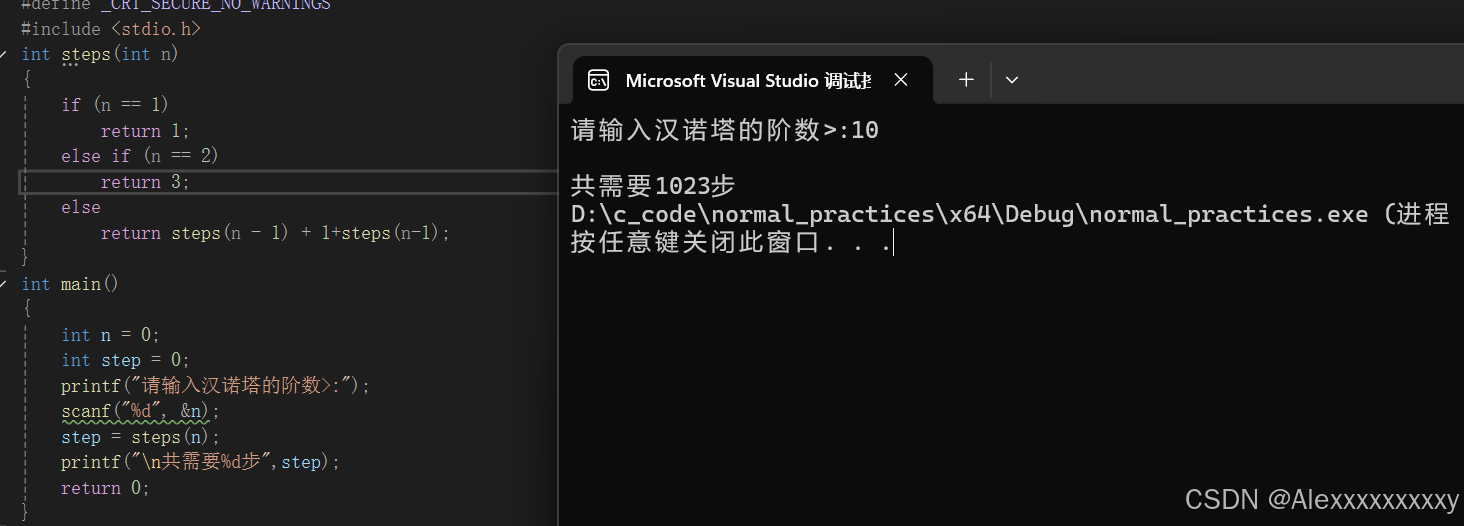
代码的改进与思考：

递归方法都有一个普遍的问题，它的效率很低，当阶数上来时，它的运行时间会变得很长。

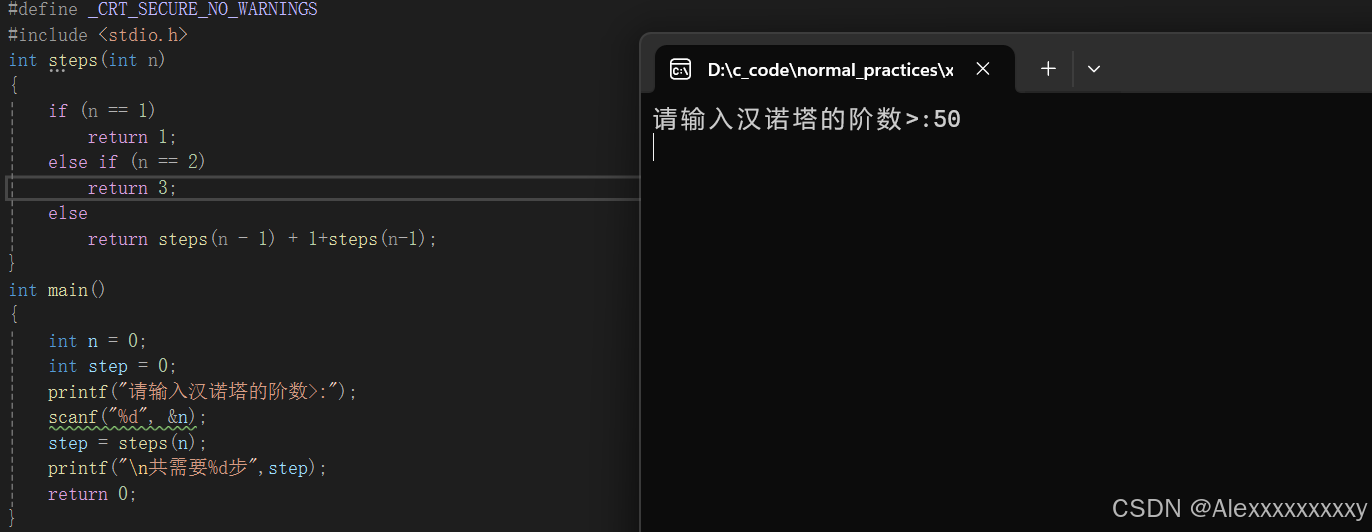
所以读者可以思考是否可以将代码优化，例如使用循环来代替递归。

总结一下，本题也是递归思想的运用，是动态规划问题的一部分，具有很好的思考价值。以上仅为本人粗略见解，若有错误敬请指正。