通过1个实例来理解算法是非常有必要的,也是比较直观的。
1 参数说明
信息素启发式因子α
α的值影响是否选择以前走过的路径,感觉有点类似粒子群算法的飞行速度,α过大会陷入局部搜索,α过小会陷入全局搜索,影响收敛速度。根据经验,α取值范围一般为[1 4]。
期望启发因子β
β的大小反应了蚁群在搜索过程中对先验知识和确定性因素的依赖程度,beta越大,收敛速度也越快,但容易陷入局部最优,β取值范围一般为[3 5]。
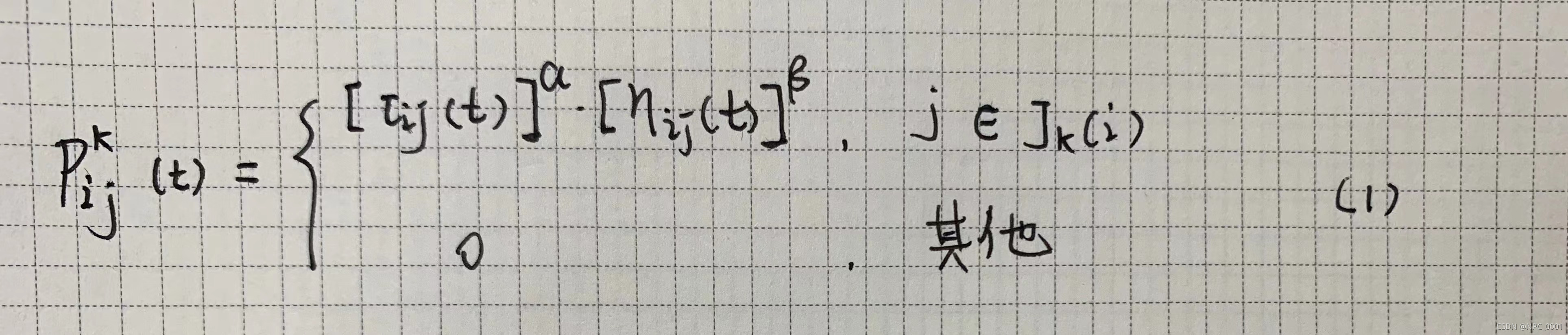
信息素蒸发系数ρ
ρ代表的路径上历史遗留信息素消失系数,取值范围[0 1]。ρ越小,信息素蒸发越慢,信息素保持就越久,路径被再次选择的可能性越大,影响全局搜索和收敛速度;ρ越大,信息素蒸发越快,容易造成无用的搜索,影响收敛速度。
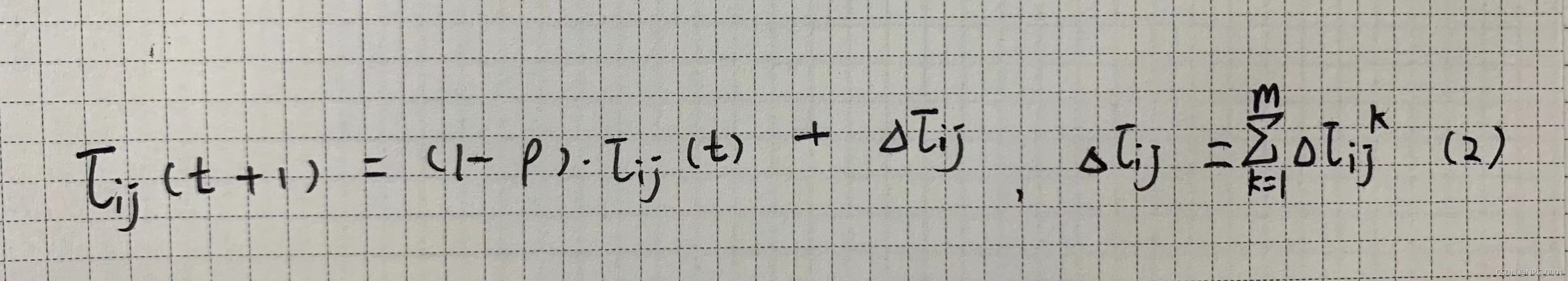
蚂蚁数量m
m一般取值为[10 50]。
信息素强度Q
影响较小,可随意取值。

最大进化代数G
一般取值为[100 500]。
2 问题描述
旅行商问题(TSP问题)。假设1个旅行商要对31个省会城市进行拜访,要求距离最短,不能重复拜访,且最终要回到出发城市。
31个城市坐标:
[1304 2312;3639 1315;4177 2244;3712 1399;3488 1535;3326 1556;
3238 1229;4196 1044;4312 790 ;4386 570 ;3007 1970;2562 1756;
2788 1491;2381 1676;1332 695 ;3715 1678;3918 2179;4061 2370;
3780 2212;3676 2578;4029 2838;4263 2931;3429 1908;3507 2376;
3394 2643;3439 3201;2935 3240;3140 3550;2545 2357;2778 2826;
2370 2975];
3 仿真过程
初始化参数
将m只蚂蚁置于n个城市
记录本次最佳路径,更新信息素,更新禁忌表
判断是否终止,输出优化结果
4 求解代码
初始化参数
%%%%%初始化参数
C = [1304 2312;3639 1315;4177 2244;3712 1399;3488 1535;3326 1556;
3238 1229;4196 1044;4312 790 ;4386 570 ;3007 1970;2562 1756;
2788 1491;2381 1676;1332 695 ;3715 1678;3918 2179;4061 2370;
3780 2212;3676 2578;4029 2838;4263 2931;3429 1908;3507 2376;
3394 2643;3439 3201;2935 3240;3140 3550;2545 2357;2778 2826;
2370 2975];
m=40;
n=size(C,1);
G=200;
Q=100;
alpha=1;
beta=5;
rho=0.2;
D=zeros(n);%任意城市间距离
for i=1:n
for j=1:n
if i~=j
D(i,j)=((C(i,1)-C(j,1))^2 + (C(i,2)-C(j,2))^2)^0.5;
else
D(i,j)=eps;%需要取倒数,值不能为0
end
end
end
eta=1./D;%启发因子
tau=ones(n);%信息素
tabu=zeros(m,n);%记录路径
rbest=zeros(G,n);%最佳路径
lbest=inf*ones(G,1);%最佳路径长度放置蚂蚁
g=1;
%%%%%算法循环
while g<=G
%%%%%将m只蚂蚁放到n个城市上
randpos=randperm(m);
for i=1:m
tabu(i,1)=mod(randpos(i),n)+1;
end蚂蚁拜访剩余城市
%%%%%m只蚂蚁基于概率选择下一个城市访问
for i=2:n
for j=1:m
visited=tabu(j,1:(i-1));%已访问
J=zeros(1,n-i+1);%待访问
P=J;%被访问概率
JN=1;
for k=1:n
if length(find(visited==k))==0
J(JN)=k;
JN=JN+1;
end
end
%%%%%待访问城市概率分布
for k=1:length(J)
P(k)=(tau(visited(end),J(k))^alpha)*(eta(visited(end),J(k))^beta);
end
P= P/sum(P);
%%%%%基于概率选择下一个访问城市
pcum=cumsum(P);
select=find(pcum>=rand);
tovisit=J(select);
tabu(j,i)=tovisit(1);
end
end
if g>1
tabu(1,:)=rbest(g-1,:);
end记录最佳路径
%%%%%记录本次迭代最佳
L=zeros(m,1);
for i=1:m
L(i)=func1(D,tabu(i,:),n);
end
lbest(g)=min(L);
pos=find(L==lbest(g));
rbest(g,:)=tabu(pos(1),:);
%%%%%路径长度函数
function result = func1(D,f,N)
len=D(f(1),f(N));
for j=2:N
len=D(f(j),f(j-1))+len;
end
result=len;
end
更新信息素和禁忌表
%%%%%更新信息素
delta_tau=zeros(n);
for i=1:m
for j=2:n
delta_tau(tabu(i,j-1),tabu(i,j))=...
delta_tau(tabu(i,j-1),tabu(i,j))+Q/L(i);
end
delta_tau(tabu(i,n),tabu(i,1))=...
delta_tau(tabu(i,n),tabu(i,1))+Q/L(i);
end
tau=(1-rho)*tau+delta_tau;
%%%%%禁忌表清零
tabu=zeros(m,n);动态输出优化过程
%%%%%历代最优
tmp_rbest=rbest(g,:);
for i=1:n-1
plot([C(tmp_rbest(i),1),C(tmp_rbest(i+1),1)],C(tmp_rbest(i),2),
C(tmp_rbest(i+1),2)],'o-');
hold on;
end
plot([C(tmp_rbest(n),1),C(tmp_rbest(1),1)],C(tmp_rbest(n),2),
C(tmp_rbest(1),2)],'ro-');
title(['最短距离:',num2str(lbest(g))]);
hold off;
pause(0.005);
g=g+1;
end
%%%%%输出优化结果
figure;
pos=find(lbest==min(lbest));
shortest_route=rbest(pos(1),:);
shortest_length=min(lbest);
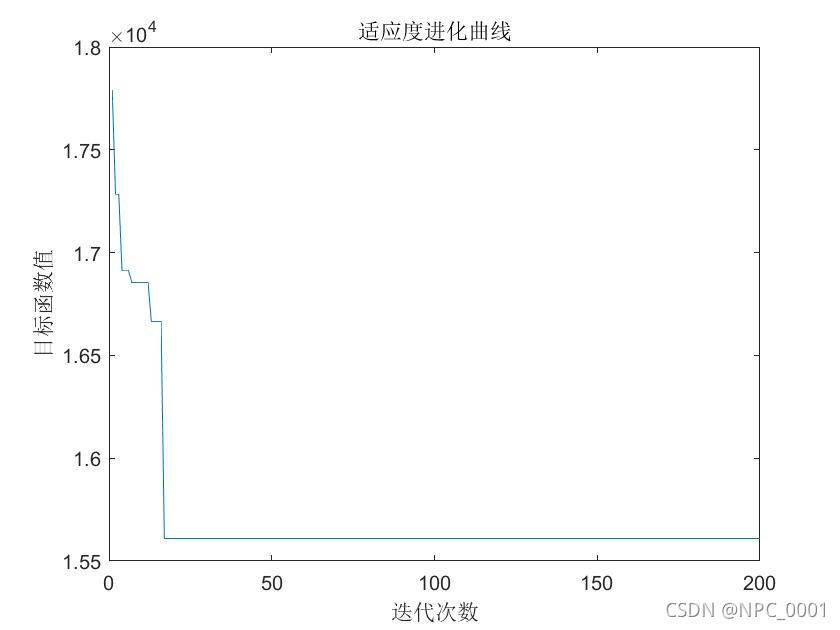
plot(lbest);
xlabel('迭代次数');
ylabel('目标函数值');
title('适应度进化曲线');5 优化结果
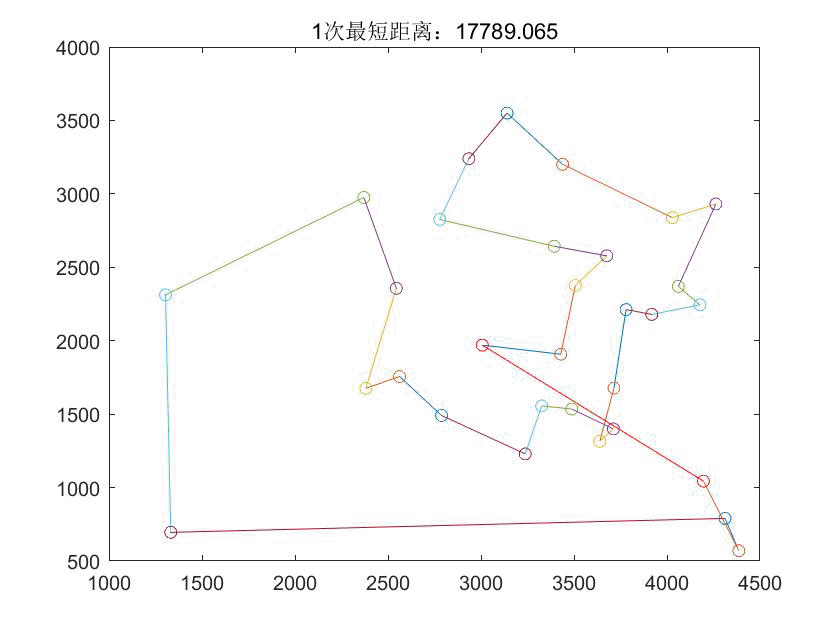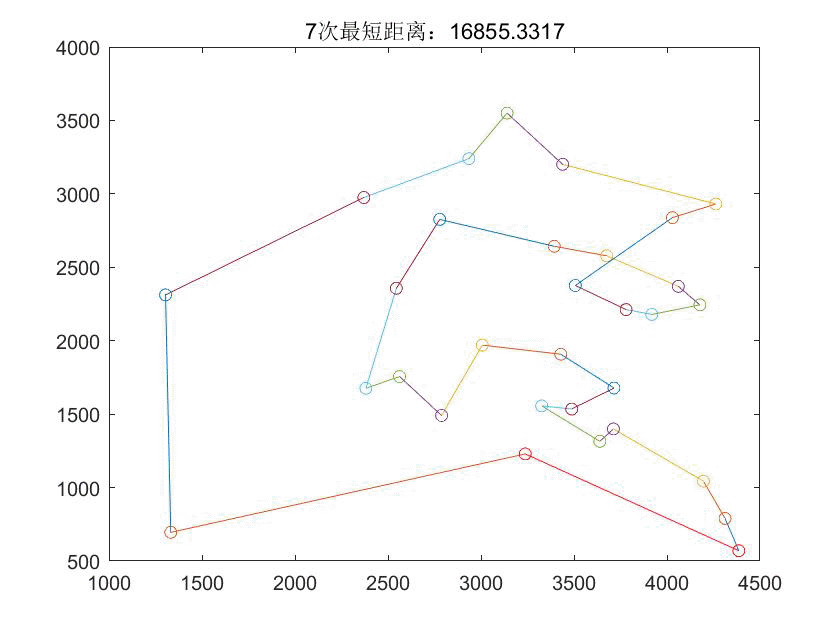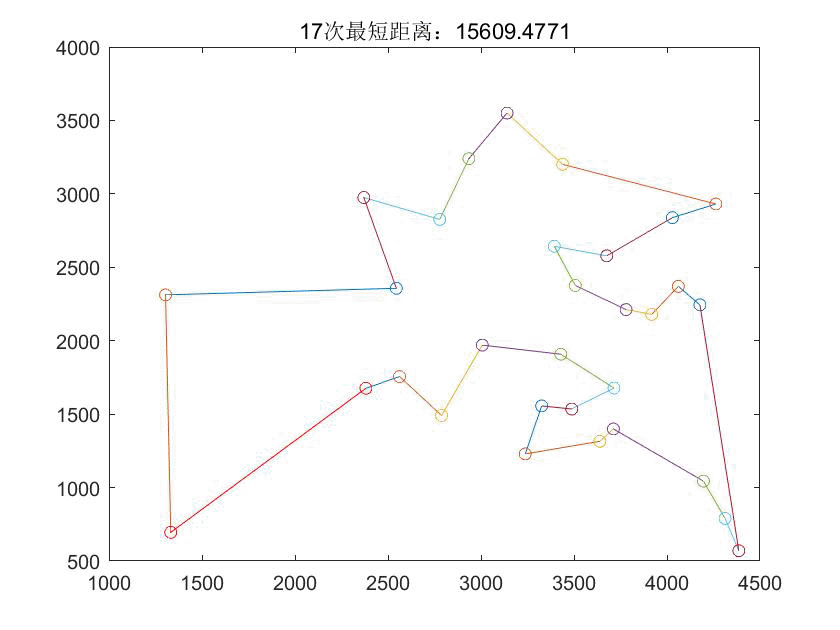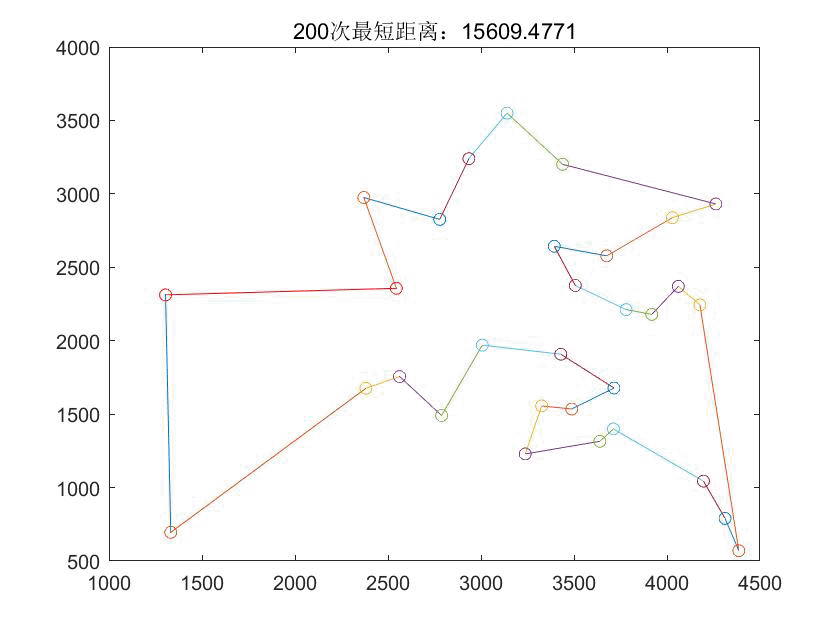








 本文通过一个实例介绍如何使用蚁群算法解决旅行商问题(TSP),详细阐述了算法参数设置、问题描述、仿真过程及求解代码,并展示了优化结果。
本文通过一个实例介绍如何使用蚁群算法解决旅行商问题(TSP),详细阐述了算法参数设置、问题描述、仿真过程及求解代码,并展示了优化结果。

















 2783
2783

 被折叠的 条评论
为什么被折叠?
被折叠的 条评论
为什么被折叠?










