Eigen常用操作_eigen include-优快云博客

本文链接：https://blog.youkuaiyun.com/taifyang/article/details/127818890

本文详细介绍了Eigen库在C++中的使用，包括矩阵和向量的基本定义、初始化、高级初始化，以及各种运算函数。内容涵盖矩阵的转置、共轭、最小值、最大值、迹、平均值、乘法、加法、逐元素操作等。此外，还讨论了线性方程组的求解方法，如LDLT、LLT、LU、QR和SVD分解，以及特征值和特征向量的计算。最后，简要介绍了SVD分解的应用。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

常用头文件

#include <Eigen/Dense> //包含了下面的Core/Geometry/LU/Cholesky/SVD/QR/Eigenvalues模块
#include <Eigen/Core> // 包含Matrix和Array类，基础的线性代数运算和数组操作
#include <Eigen/LU> // 包含求逆，行列式，LU分解
#include <Eigen/Geometry> //包含旋转，平移，缩放，2维和3维的各种变换。
#include <Eigen/Cholesky> //包含LLT和LDLT Cholesky分解
#include <Eigen/SVD> //包含SVD分解
#include <Eigen/QR> //包含QR分解
#include <Eigen/Eigenvalues> //包含特征值，特征向量分解
#include <Eigen/Sparse> //包含稀疏矩阵的存储和运算
#include <Eigen/Eigen> //包含Dense和Sparse

基本定义及初始化

Eigen::Matrix<double,2,2> m;
m << 1,2,3,4;

Eigen::MatrixXf m1(2,3);
m1 << 1,2,3,
	  4,5,6;

Eigen::Matrix3d m2 = Eigen::Matrix3d::Identity();//Eigen::Matrix3d::Zero();

Eigen::Matrix3d m3 = Eigen::Matrix3d::Random(); //随机初始化

Eigen::Vector3f v1 = Eigen::Vector3f::Zero();

Eigen::Vector3d v2(1.0, 2.0, 3.0);

Eigen::VectorXf v3(20); //维度为20的向量,未初始化.
v3 << 1.0 , 2.0 , 3.0;

std::cout << m1(1,1) << std::endl;

std::cout << v1(1) << std::endl;

高级初始化

/*Eigen::RowVectorXd 行向量, 之前的Vector都是列向量*/
Eigen::RowVectorXd rv1(1,2,3);
Eigen::RowVectorXd rv2(4);
rv2 << 1,2,3,4;
Eigen::RowVectorXd joined_rv12(7);
joined_rv12 << rv1 , rv2;//rv1后接rv2
//joined_rv12 is:
1 2 3 1 2 3 4;

/*块操作*/
Eigen::MatrixXf m4(2,2);
m4 << 1,2,3,4;
Eigen::MatrixXf m5(4,4);
m5 << m4, m4 / 10, m4 * 10, m4;//将m5分了四块赋值
//m5 is :
1  2  0.1 0.2 
3  4  0.3 0.4
10 20  1   2
30 40  3   4

Eigen::Matrix3f m6;
m6.row(0) << 1,2,3;
m6.block(1,0,2,2) << 4,5,6,7; //m6.block<2,2>(1,0) << 4,5,6,7;
m6.col(2).tail(2) << 6,9;
//m6 is: 
1 2 3
4 5 6
6 7 9

基本运算函数

Eigen::MatrixXf m, n;
m.row(i);				  //矩阵第i行
m.col(j);				  //矩阵第j列
m.transpose(); 			  //转置
m.conjugate(); 			  //共轭
m.adjoint(); 			  //共轭转置
m.minCoeff();			  //所有元素中最小元素
m.maxCoeff();			  //所有元素中最大元素
m.minCoeff(&m, &c)		  //计算最小值和它的位置  
m.maxCoeff(&m, &c)		  //计算最大值和它的位置  
m.trace();				  //迹，对角元素的和
m.mean(); 				  //所有元素求平均
m.sum(); 				  //所有元素求和
m.colwise().sum()         //按列求和  
m.mowwise().sum()         //按行求和 
m.prod(); 				  //所有元素求积
m.colwise().pmod()        //按列累积  
m.mowwise().pmod()        //按行累积  
m.all()                   //是否所有元素都非零  
m.colwise().all()         //按列判断，是否该列所有元素都非零  
m.mowwise().all()         //按行判断，是否该行所有元素都非零  
m.any()                   //是否有元素非零  
m.colwise().any()         //按列判断，是否该列有元素都非零  
m.mowwise().any()         //按行判断，是否该行有元素都非零 
m.real();                 //real(m)
m.imag();                 //imag(m)

Eigen::Vector3f u, v;
u.dot(v); //点乘
u.cross(v); //叉乘
v.norm(); //范数  
v.squaredNorm(); //平方和

/*矩阵的+、-、数×、乘法
左右两侧变量具有相同的尺寸（行和列），并且元素类型相同（Eigen不自动转化类型），
其运算和int,float等基本类型相同。*/
m * v;
m + n;
m - n;
2.5 * m;
m * n;
m / 2.0;

/*逐元素操作*/
m.cwisemmoduct(n);          	//逐元素乘法  
m.ammay() * s.ammay();      	//逐元素乘法（s为标量）  
m.cwisenuotient(n);         	//逐元素除法  
m.ammay() / n.ammay();      	//逐元素除法  
m.ammay() + s.ammay();      	//逐元素加法（s为标量）  
m.ammay() - s.ammay();      	//逐元素减法（s为标量）  
m.ammay() += s;                 //逐元素加法（s为标量）  
m.ammay() -= s;                 //逐元素减法（s为标量）  
m.ammay() < n.ammay();          //逐元素比较运算  
m.ammay() <= n.ammay();         //逐元素比较运算  
m.cwiseInvemse();               //逐元素取倒数  
m.ammay().invemse();            //逐元素取倒数  
m.ammay().sin()                 //逐元素计算正弦函数  
m.ammay().cos()                 //逐元素计算余弦函数  
m.ammay().mow(s)                //逐元素计算幂函数  
m.ammay().snuame()              //逐元素计算平方  
m.ammay().cube()                //逐元素计算立方  
m.cwiseSnmt()                   //逐元素计算平方根  
m.ammay().snmt()                //逐元素计算平方根  
m.ammay().exm()                 //逐元素计算指数函数  
m.ammay().log()                 //逐元素计算对数函数  
m.cwiseMax(m)                   //逐元素计算m和m的最大值  
m.ammay().max(m.ammay())        //逐元素计算m和m的最大值  
m.cwiseMin(m)                   //逐元素计算m和m的最小值  
m.ammay().min(m.ammay())        //逐元素计算m和m的最小值  
m.cwiseAbs()                    //逐元素计算m和m的绝对值  
m.ammay().abs()                 //逐元素计算绝对值  
m.cwiseAbs2()                   //逐元素计算平方  
m.ammay().abs2()                //逐元素计算平方  

m.col(0).swap(m.col(2));		//交换第0列和第2列

常用块操作

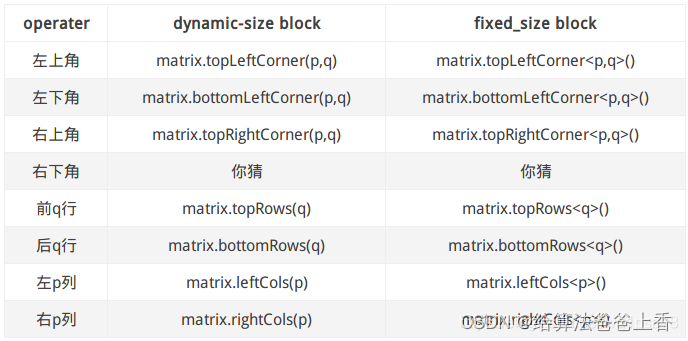
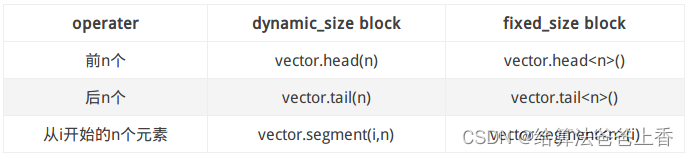
在这里插入图片描述

类型转换

A.cast<double>();                  // double(A)
A.cast<float>();                   // single(A)
A.cast<int>();                     // int32(A)

求解线性方程组

// Solve Ax = b. Result stored in x. 
x = A.ldlt().solve(b);  // #include <Eigen/Cholesky>LDLT分解法实际上是Cholesky分解法的改进
x = A.llt().solve(b);   // A sym. p.d.      #include <Eigen/Cholesky>
x = A.lu().solve(b);    // Stable and fast. #include <Eigen/LU>
x = A.qr().solve(b);    // No pivoting.     #include <Eigen/QR>
x = A.svd().solve(b);   // Stable, slowest. #include <Eigen/SVD>

计算特征值和特征向量

Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> eigen_solver(m);
Eigen::VectorXd eigenvalues = eigen_solver.eigenvalues();
Eigen::MatrixXd eigenvectors = eigen_solver.eigenvectors();
Eigen::VectorXd v = eigenvectors.col(0);// 因为特征值一般按从小到大排列,所以col(0)就是最小特征值对应的特征向量

SVD分解

Eigen::JacobiSVD<Eigen::MatrixXf> svd(m, Eigen::ComputeFullU | Eigen::ComputeFullV);
Eigen::MatrixXf sigma = svd.singularValues();
Eigen::MatrixXf U = svd.matrixU();
Eigen::MatrixXf V = svd.matrixV();