课程12. 神经网络

到目前为止，我们讨论的都是经典的机器学习算法。今天，我们将探讨机器学习如何超越经典模型，通过开发一种全新的模型——神经网络——发展成为深度学习。

线性回归的作用？

让我们回顾一下什么是线性回归。它是一种模型，通过为描述对象的每个特征生成权重，从而对对象的某些特性进行合理的预测。

从某种意义上说，这些权重可以被视为给定特征对最终决策的重要性。让我们来看一个经典的例子：

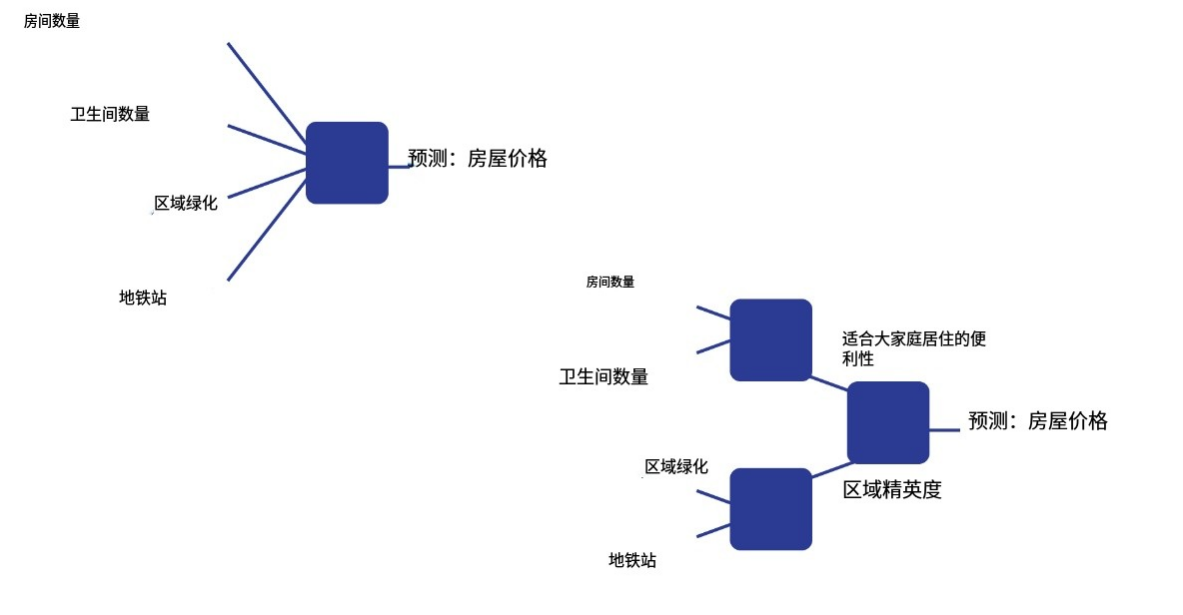
假设我们需要根据房屋的某些特征来评估其价值。这些特征包括：

• 房间数量，

• 浴室数量，

• 该地区学校的平均绩点（该特征可以被视为对这些学校质量的评估），

• 该地区的绿化率，

• 地铁站，

• 该地区的平均房价。

标准的线性回归尝试基于我们已知的这些基本特征进行预测。但是，这些特征的某些组合可以提供比基本特征更丰富的信息。例如，如果我们知道一栋房子有多少个房间和浴室，就可以预测它对大家庭的居住舒适度。平均学校成绩和该地区的绿化率等信息可以用来推断该社区是否适合养育孩子。地铁站和平均房价可以用来判断该社区的档次。

利用这种方法，我们可以生成更高层次的特征描述。这些特征能够更好地描述我们的对象，就像从原始描述中提取出最相关的信息一样。我们如何提取这些特征呢？

假设我们需要从 N 个低层次特征中获得 M 个高层次特征。这可以通过训练一个独立的线性回归模型来预测每个高层次特征来实现。从获得的特征中，我们可以创建越来越高层次的特征，直到我们最终决定停止并训练线性回归，从而得到最终答案。

罗森布拉特的感知器

20世纪50年代，美国科学家弗兰克·罗森布拉特致力于构建人类视觉图像识别的数学模型。

他的研究得出以下结论：

• 物体识别基于特定感受器组合的兴奋，这种兴奋随后通过神经元传递。

• 神经元是一种细胞，可以处于两种状态：兴奋状态和静息状态。一个神经元有N个输入通道，兴奋信号可以通过这些通道传递到神经元；还有一个输出通道，神经元可以通过该通道将冲动传递给其他神经元。兴奋的神经元会传递冲动，而静息的神经元则不会。

• 当通过输入通道到达的总电荷超过某个阈值时，神经元就会兴奋。

• 神经元以三层结构相互连接：第一层是感觉层，接收来自环境中各个感受器的兴奋信号；第二层是隐藏层，其功能遵循上述机制；第三层是识别层。它由N个神经元组成，每个神经元都可以处于兴奋或静息状态。每个神经元对特定的信号模式做出反应，而兴奋状态则由信号决定。

---

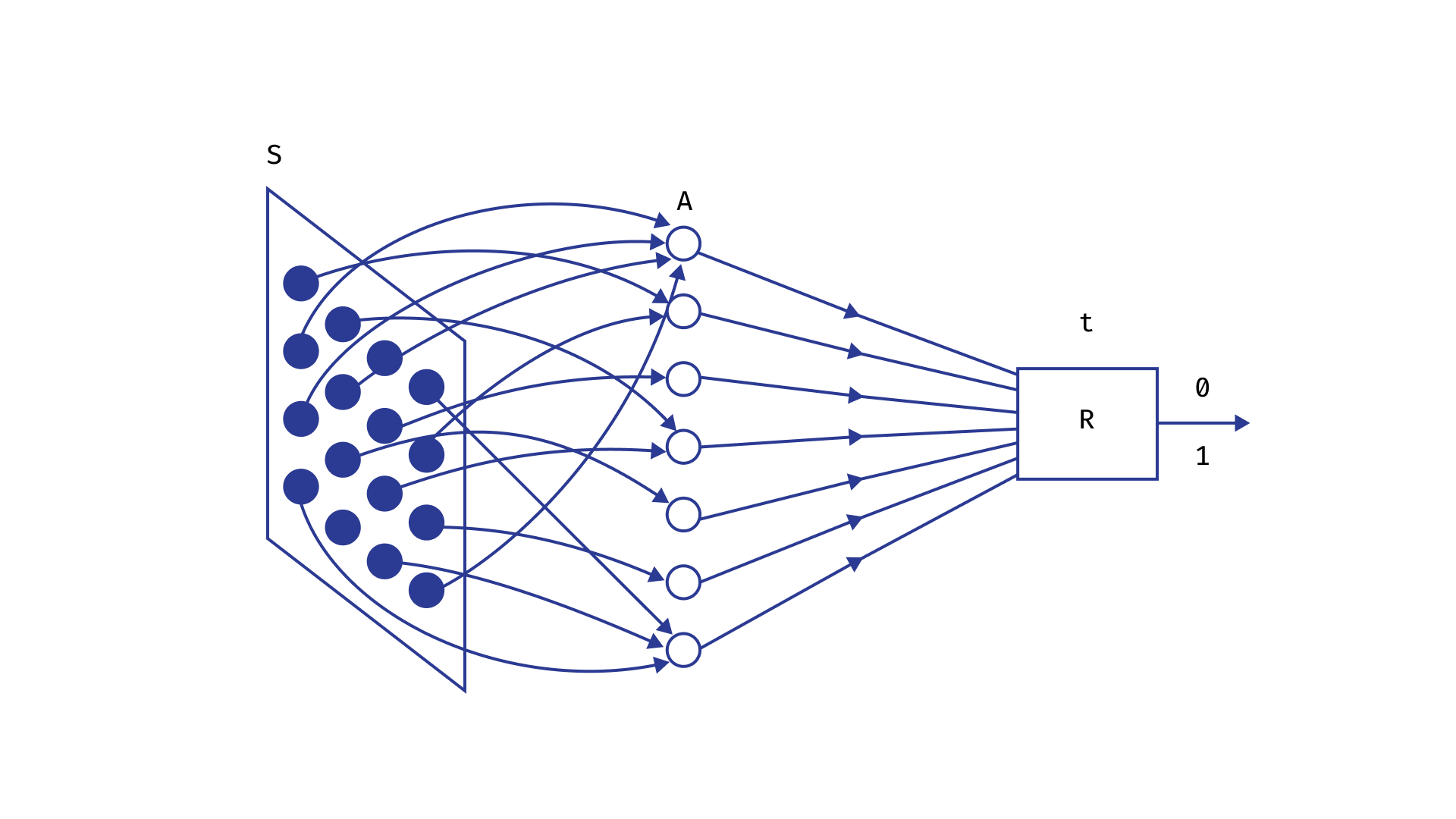
该范式中单个神经元的运行与线性回归非常相似，但有一些改进。

令 ${\lambda }_i$ 为到达神经元第 i 个输入通道的信号。则输出信号定义为 output($\vec{\lambda }$) = [∑${\lambda }_i$ > β]，其中 β 为该神经元的激活阈值（即神经元进入兴奋状态的电荷阈值）。

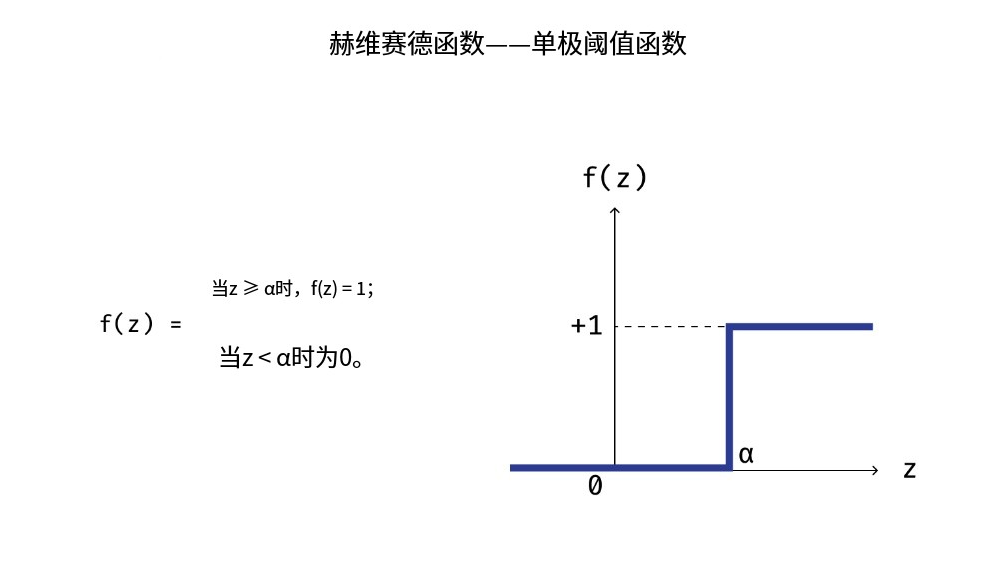
让我们注意两个与我们对这一过程物理机制的理解相对应的细节。

首先，每个神经元的每个输入和输出通道可能都有其自身的电阻，这会影响沿通道传输的脉冲。我们可以通过为每个输入脉冲引入权重来对这一过程进行建模。也就是说，output($\vec{\lambda }$) = [∑$w_i{\lambda }_i$ > β]，其中 $w_i$ 是表征第 i 个输入通道电阻的权重。

其次，真实的神经元在传播电脉冲时不太可能如此绝对，以至于只有两种状态：0 和 1。最有可能的情况是，神经元总是会向后续层传递特定的脉冲，但这个脉冲高度依赖于指定的输入脉冲总和。这种输出函数的图像很可能与阈值函数非常相似。也许你们中的一些人已经猜到，熟悉的 sigmoid 函数就是这种函数的一个很好的例子。

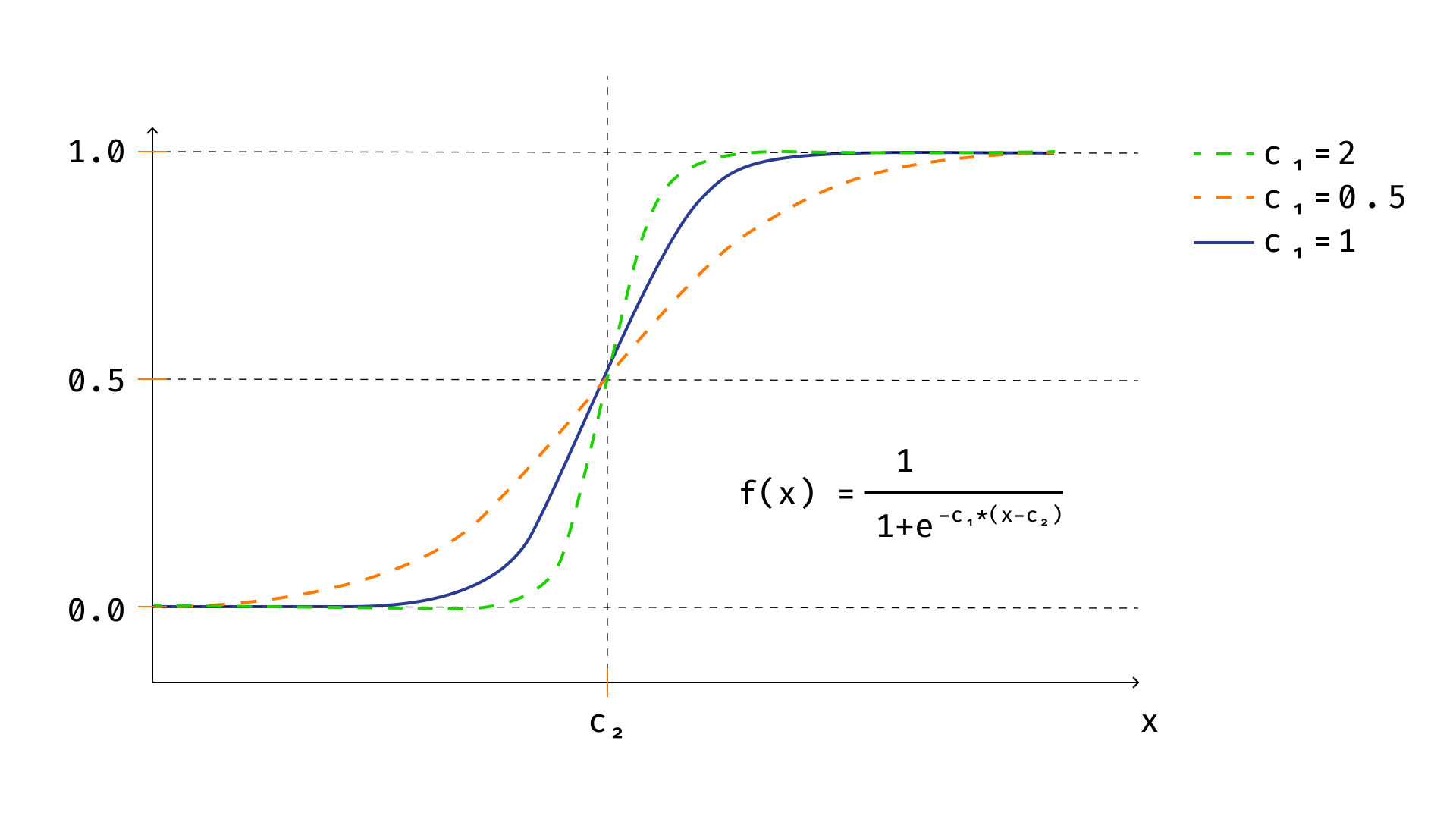
如果我们用 sigmoid 函数替换阈值函数，神经元的数学模型最终会转化为逻辑回归模型。实际上，$$output(\vec{\lambda })=\sigma (\sum w_i{\lambda }_i)$$

一般来说，其他函数也可以替换 sigmoid 函数。这类函数被称为激活函数。经典的激活函数包括双曲正切函数、线性函数和 ReLU 函数。

异或(XOR)问题

线性能解决？

这种方法能够自动帮助我们解决一些简单的线性模型无法解决的问题。

其中一个问题在上世纪中期被发现，几乎彻底摧毁了公众对机器学习的看法。
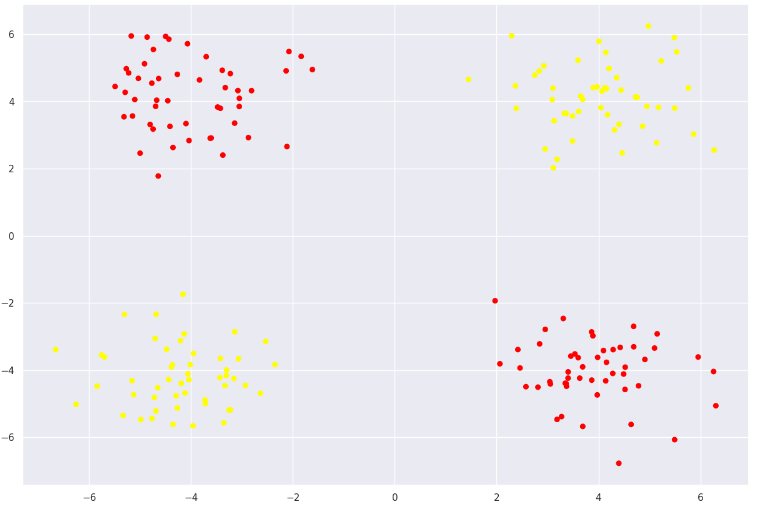
我们来创建一下数据集：

import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

sns.set_theme()

rng = np.random.RandomState(0)
X1 = rng.randn(50, 2) + np.array([4,4])
X2 = rng.randn(50, 2) + np.array([-4,4])
X3 = rng.randn(50, 2) + np.array([4,-4])
X4 = rng.randn(50, 2) + np.array([-4,-4])
X = np.concatenate([X1,X2,X3,X4])
classes = np.sign(X[:, 0]*X[:, 1])

plt.figure(figsize=(15,10))
plt.scatter(X[:, 0], X[:, 1], s=30, c=classes, cmap=plt.cm.autumn)

输出：

import warnings
warnings.filterwarnings('ignore')
def plot_gradient(clf, X, y, plot_title):
  clf.fit(X, y)

  x_mesh, y_mesh = np.meshgrid(np.linspace(-8, 8, 50), np.linspace(-8, 8, 50))
  to_forecast = np.vstack((x_mesh.ravel(), y_mesh.ravel()))
  Z = clf.predict_proba(to_forecast.T)[:, 1]
  Z = Z.reshape(x_mesh.shape)

  b_left= x_mesh.min()
  b_right = x_mesh.max()
  b_down = y_mesh.min()
  b_up = y_mesh.max()

  image = plt.imshow(Z,
                     aspect='auto',
                     origin='lower',
                     cmap=plt.cm.PuOr_r,
                     interpolation='quadric',
                     extent=(b_left, b_right, b_down, b_up))

  contours = plt.contour(x_mesh, y_mesh, Z, levels=[0], linewidths=2, linetypes='--')
  plt.scatter(X[:, 0], X[:, 1], s=30, c=y, cmap=plt.cm.autumn)
  plt.axis([-8, 8, -8, 8])
  plt.colorbar(image)
  plt.title(plot_title, fontsize=20);

from sklearn.linear_model import LogisticRegression
plt.figure(figsize=(15,10))
plot_gradient(LogisticRegression(penalty='elasticnet', solver='saga', l1_ratio=0.5), X, classes, "Logistic Regression, XOR problem")

输出：

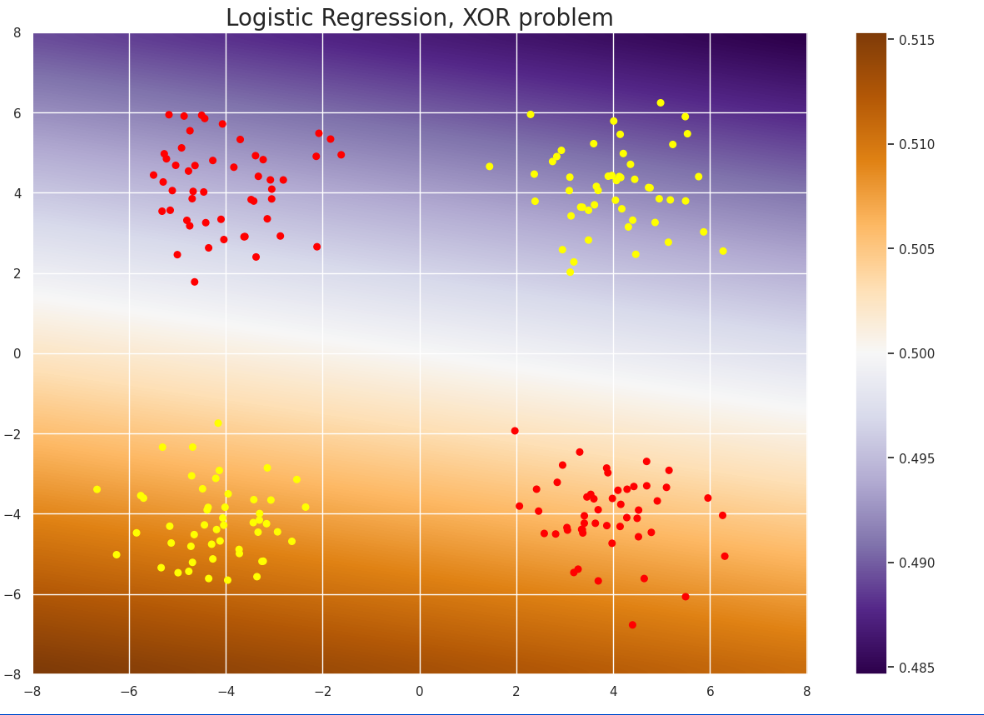
我们该怎么办呢？

让我们尝试将三个逻辑回归模型合并成以下结构：

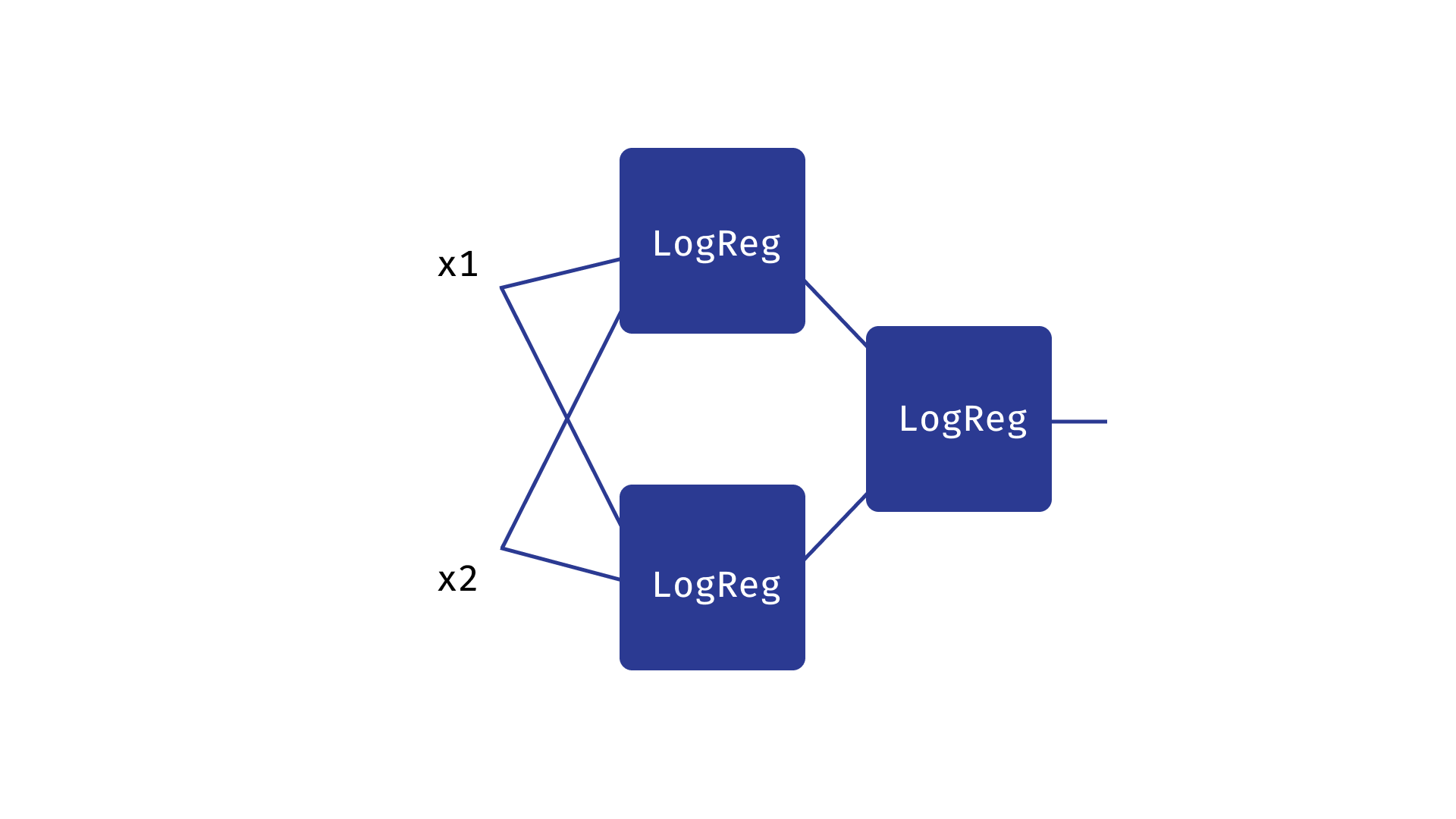
请注意以下细节：

1. 我们得到的是三个逻辑回归的串联，它们可以提取高层特征并将其用于最终预测，如本课第一节所述。

2. 这种结构类似于 Rosenblatt 模型中三个神经元的组合，如本课第二节所述。

3. 我们可以预期，第一层构建的逻辑回归对应于将平面初始划分为三个类别，而最终的逻辑回归会将它们的预测结果合并为一个单一的预测单元。

class trinity_of_lr:
  def __init__(self):
    self.lr_1 = LogisticRegression()
    self.lr_2 = LogisticRegression()
    self.lr_3 = LogisticRegression()

  def fit(self, X, y):
    y_1 = (X[:,0] > 0).astype(int) * (X[:,1] < 0).astype(int)
    y_2 = (X[:,0] < 0).astype(int) * (X[:,1] > 0).astype(int)

    self.lr_1.fit(X,y_1)
    self.lr_2.fit(X,y_2)

    probas_1 = self.lr_1.predict_proba(X)
    probas_2 = self.lr_2.predict_proba(X)

    x_3 = np.concatenate([probas_1, probas_2], axis=-1)

    self.lr_3.fit(x_3,y)

  def predict(self, X):
    probas_1 = self.lr_1.predict_proba(X)
    probas_2 = self.lr_2.predict_proba(X)
    x_3 = np.concatenate([probas_1, probas_2], axis=-1)

    preds = self.lr_3.predict(x_3)
    return preds


  def predict_proba(self, X):
    probas_1 = self.lr_1.predict_proba(X)
    probas_2 = self.lr_2.predict_proba(X)
    x_3 = np.concatenate([probas_1, probas_2], axis=-1)

    preds = self.lr_3.predict_proba(x_3)
    return preds

plt.figure(figsize=(15,10))
plot_gradient(trinity_of_lr(), X, classes, "XOR problem solution")

输出：

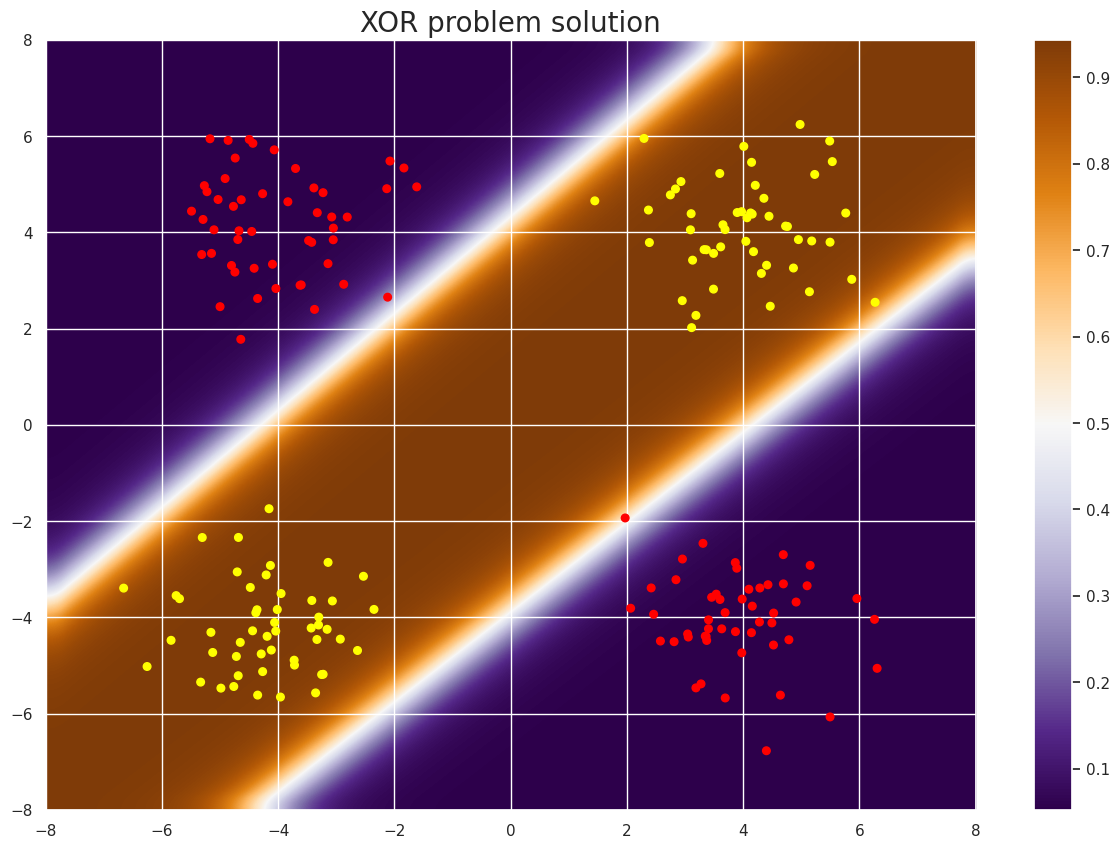
解决了异或问题！

通过结合三个逻辑回归模型，我们构建了一个比任何线性模型都更复杂的超曲面分离模型。

该模型是一个简单的两层神经网络示例。

神经网络可以更大更深。有时，神经元的数量（即这些逻辑回归模型或其改进版本）可达数十万。层数通常也更多。此外，还有一些特殊类型的神经网络，它们以不同的方式组织计算，但这又是另一个话题了。

训练神经网络的关键在于选择最优参数。这通常使用梯度下降法，我们在第三讲讨论逻辑回归时已经提到过。如果您决定深入研究神经网络，您需要理解的一个问题是：当神经网络的层数非常多时，如何计算其内部层参数的导数。

神经网络

优势

• 与传统机器学习算法相比，神经网络能够“记住”数据中更为复杂的依赖关系。

• 神经网络比大多数传统机器学习算法更具容量（即，在其他条件相同的情况下，它们包含更多可训练参数）。

• 神经网络有很多不同的类型，每种类型都适用于解决特定的问题。

问题

• 如何训练神经网络？在给出的例子中，我们预先知道数据的结构，并基于此选择了一种训练机制。但一般来说，我们应该怎么做呢？

• 我们应该使用哪些神经网络库？

• 神经网络有哪些类型？

• 训练神经网络时会遇到哪些挑战？

这些问题的解决可以看我另一个专栏深度学习，讲深入探讨神经网络的应用。

示例

神经网络可以对数据中的非线性关系进行建模！

让我们来看另一个例子，在这个例子中，我们无法用线性模型找到解决方案，但神经网络可以帮助我们克服这个难题。

让我们尝试对余弦函数进行建模！

from sklearn.neural_network import MLPRegressor
import numpy as np
import matplotlib.pyplot as plt


X_train = np.random.uniform(-6,6, size=(500,1))
y_train = np.cos(X_train)

X_test = np.random.uniform(-6,6, size=(100,1))
y_test = np.cos(X_test)

plt.figure(figsize=(15,10))
plt.scatter(X_train,y_train,label='train')
plt.scatter(X_test,y_test,label='test')
plt.legend()

输出：

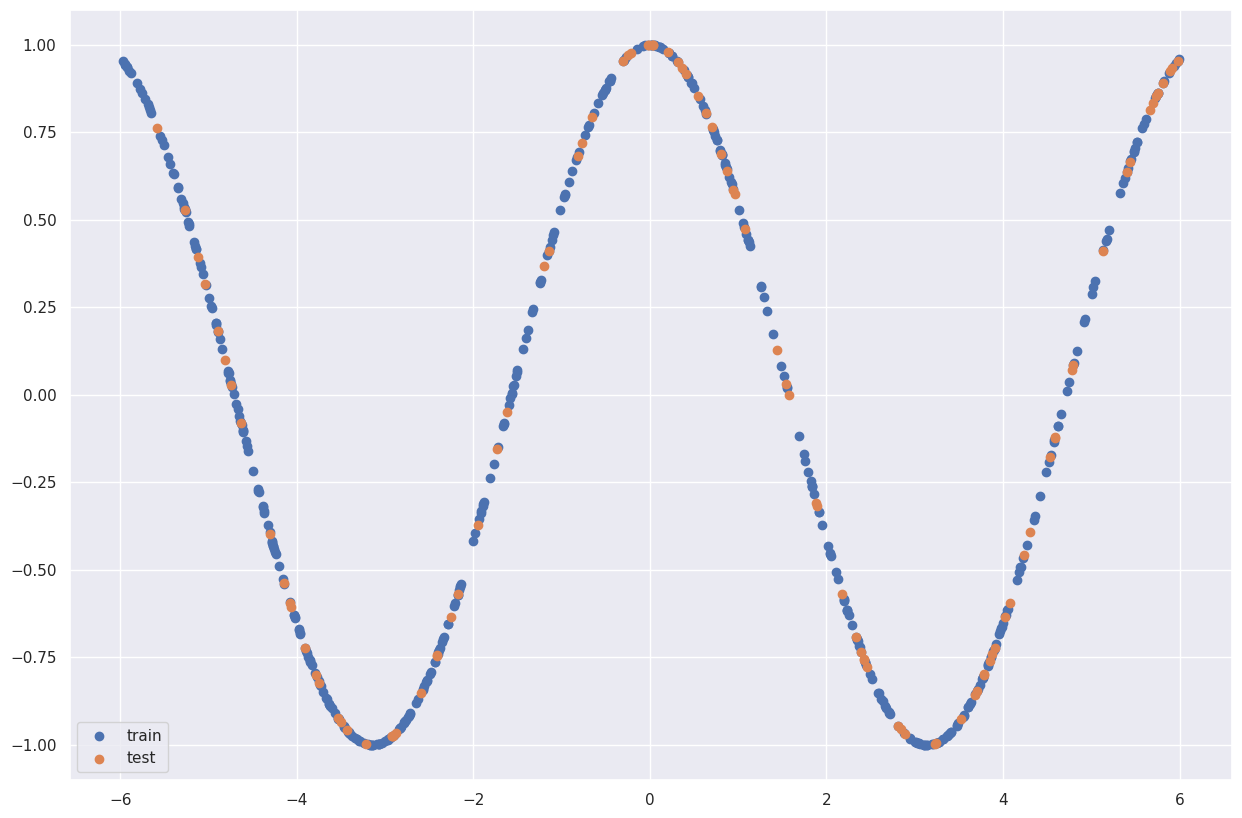
NN = MLPRegressor(hidden_layer_sizes=[3,2], activation='relu').fit(X_train,y_train)

grid = np.linspace(-6,6,1000)
preds = NN.predict(grid.reshape(-1,1))

plt.figure(figsize=(15,10))
plt.scatter(X_train,y_train,label='train')
plt.scatter(X_test,y_test,label='test')
plt.plot(grid, preds, label='NN prediction', c='r')
plt.legend()

输出：

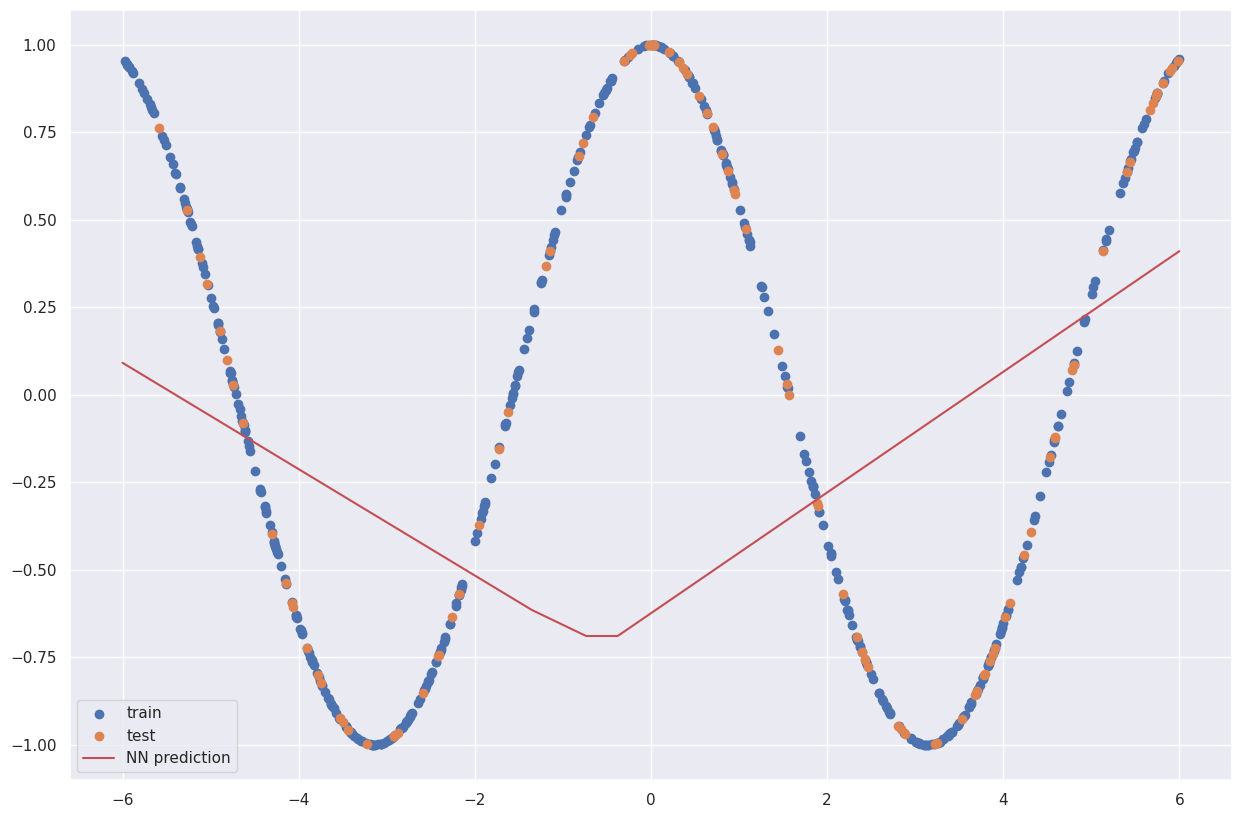
预测结果不太理想。为什么？因为我们的模型可能神经元数量太少了。我们来增加神经元数量！

NN = MLPRegressor(hidden_layer_sizes=[30,20], activation='relu').fit(X_train,y_train)

preds = NN.predict(grid.reshape(-1,1))

plt.figure(figsize=(15,10))
plt.scatter(X_train,y_train,label='train')
plt.scatter(X_test,y_test,label='test')
plt.plot(grid, preds, label='NN prediction', c='r')
plt.legend()

输出：

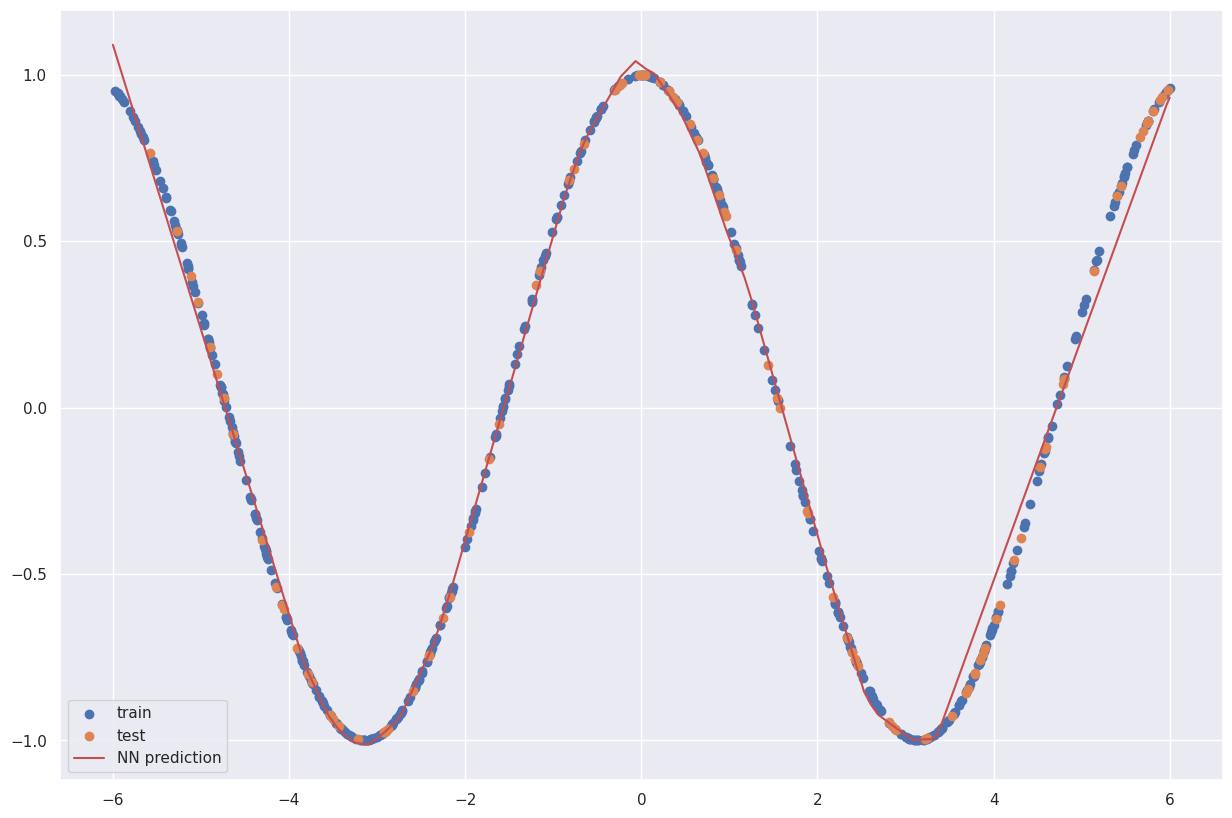
情况好转了一些。让我们把它做得更大！

NN = MLPRegressor(hidden_layer_sizes=[1000, 200], activation='relu').fit(X_train,y_train)

preds = NN.predict(grid.reshape(-1,1))

plt.figure(figsize=(15,10))
plt.scatter(X_train,y_train,label='train')
plt.scatter(X_test,y_test,label='test')
plt.plot(grid, preds, label='NN prediction', c='r')
plt.legend()

输出：

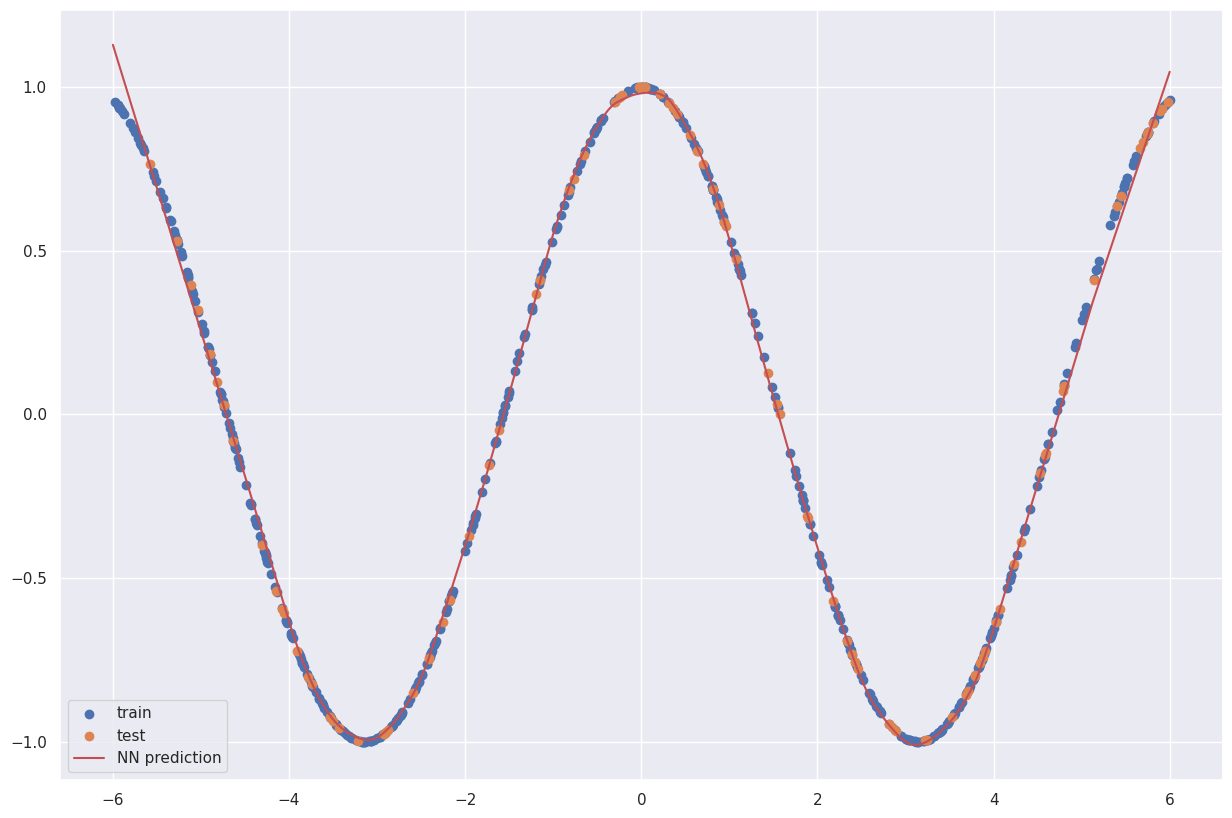
神经网络可以很好地逼近余弦函数！

一个重要的数学命题是：任何函数都可以用一个具有足够神经元数量的单层神经网络来逼近。

但这个命题也有其不足之处。它告诉我们逼近是可能的，但并没有告诉我们如何构建它。训练神经网络的艺术就在于克服这种复杂性（即选择合适的架构、最优的超参数、神经元数量、层数等等）。我们不能用一个巨大的单层来构建全连接神经网络，因为这样的网络会严重过拟合。

神经网络是具有大量可训练参数的复杂函数，我们必须对这些参数进行最优选择。

回到我们的例子：你可能会认为经典的机器学习也有一些模型能够解决这个问题。例如，度量回归方法。

from sklearn.neighbors import KNeighborsRegressor
KNN = KNeighborsRegressor().fit(X_train,y_train)

preds_KNN = KNN.predict(grid.reshape(-1,1))

plt.figure(figsize=(15,10))
plt.scatter(X_train,y_train,label='train')
plt.scatter(X_test,y_test,label='test')
plt.plot(grid, preds_KNN, label='KNN prediction', c='r')
plt.legend()

输出：

或者决策树

from sklearn.tree import DecisionTreeRegressor
tree = DecisionTreeRegressor().fit(X_train,y_train)

preds_tree = tree.predict(grid.reshape(-1,1))

plt.figure(figsize=(15,10))
plt.scatter(X_train,y_train,label='train')
plt.scatter(X_test,y_test,label='test')
plt.plot(grid, preds_tree, label='tree prediction', c='r')
plt.legend()

输出：

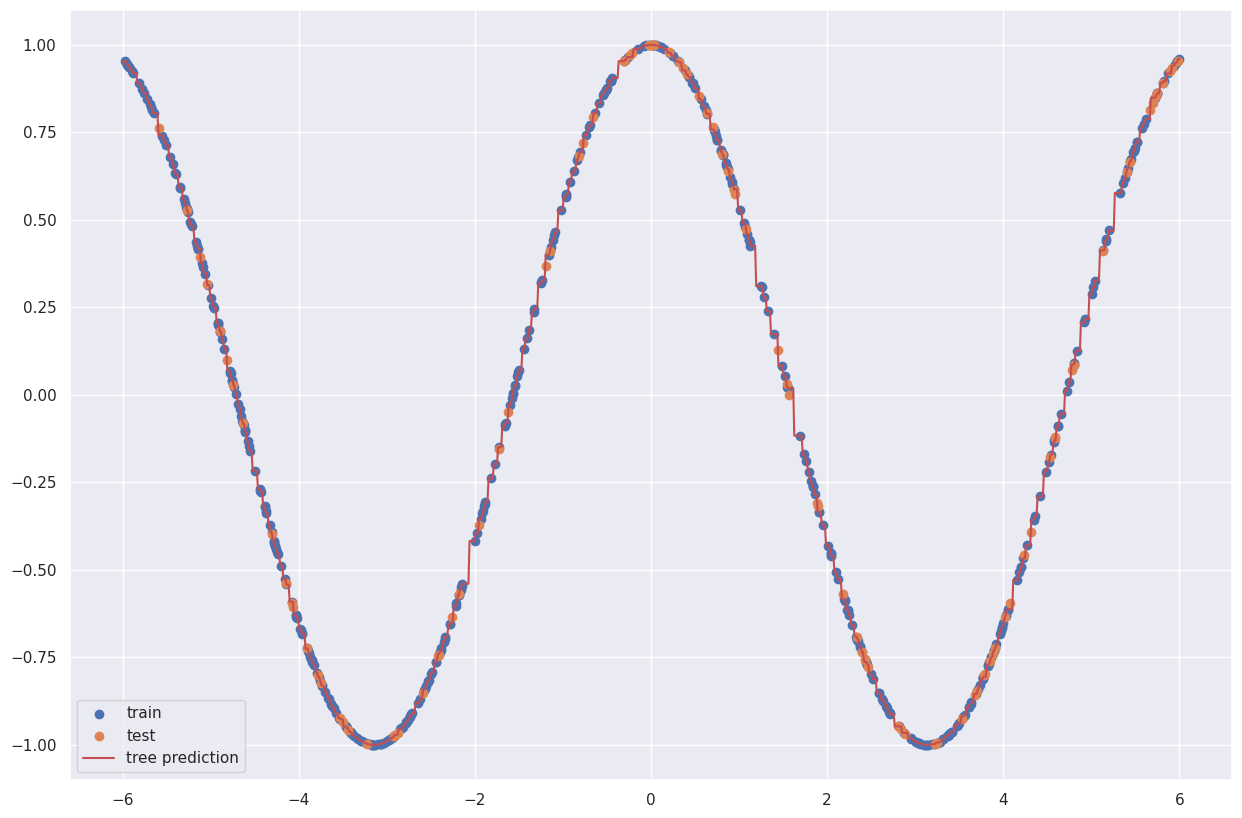
或者甚至是梯度提升

from sklearn.ensemble import GradientBoostingRegressor
grad_boost = GradientBoostingRegressor().fit(X_train,y_train)

preds_grad_boost = grad_boost.predict(grid.reshape(-1,1))

plt.figure(figsize=(15,10))
plt.scatter(X_train,y_train,label='train')
plt.scatter(X_test,y_test,label='test')
plt.plot(grid, preds_grad_boost, label='grad_boost prediction', c='r')
plt.legend()

输出：

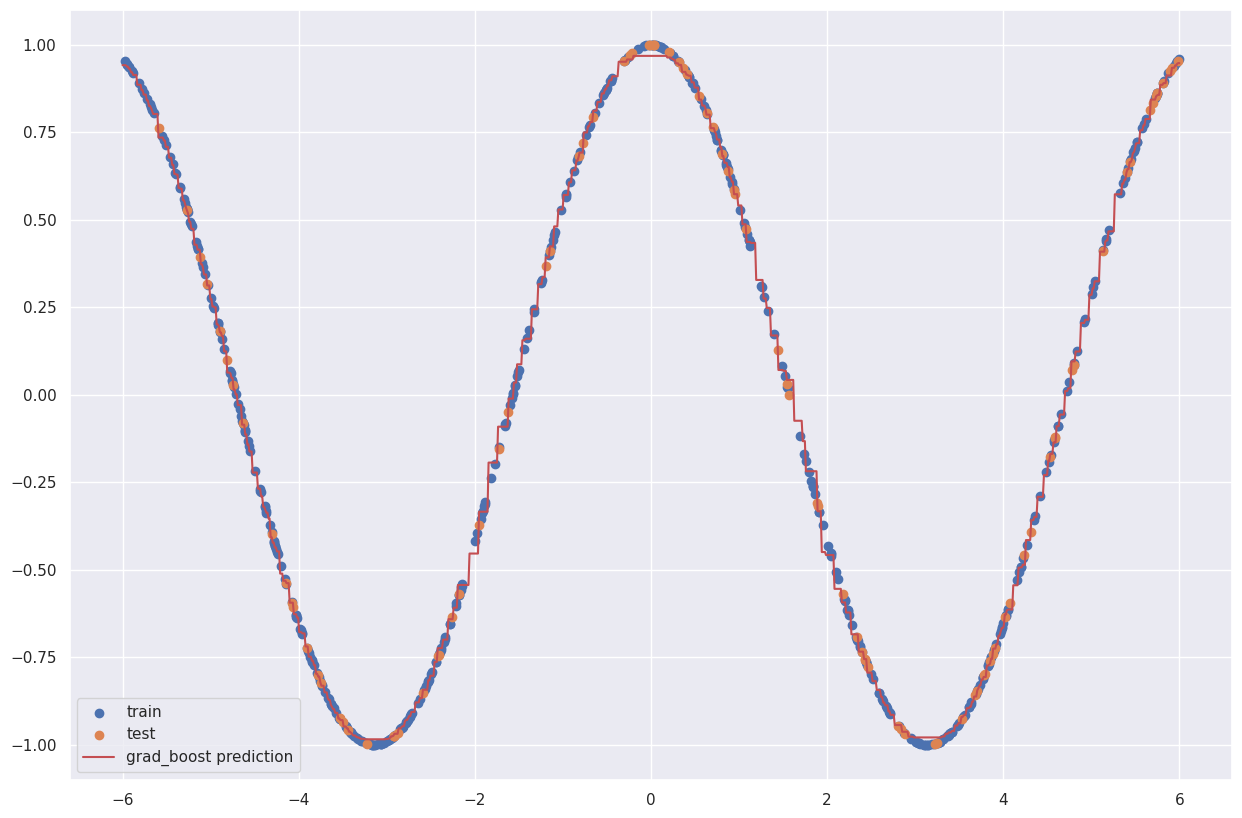
神经网络的优势显而易见，尤其是当所有曲线都绘制在一张图表上时。

plt.figure(figsize=(15,10))

cos = np.cos(grid)
plt.plot(grid, preds_grad_boost, label='grad_boost prediction')
plt.plot(grid, preds_tree, label='tree prediction')
plt.plot(grid, preds_KNN, label='KNN prediction')
plt.plot(grid, preds, label='NN prediction')
plt.plot(grid, cos, label='Target')
plt.legend()

输出：

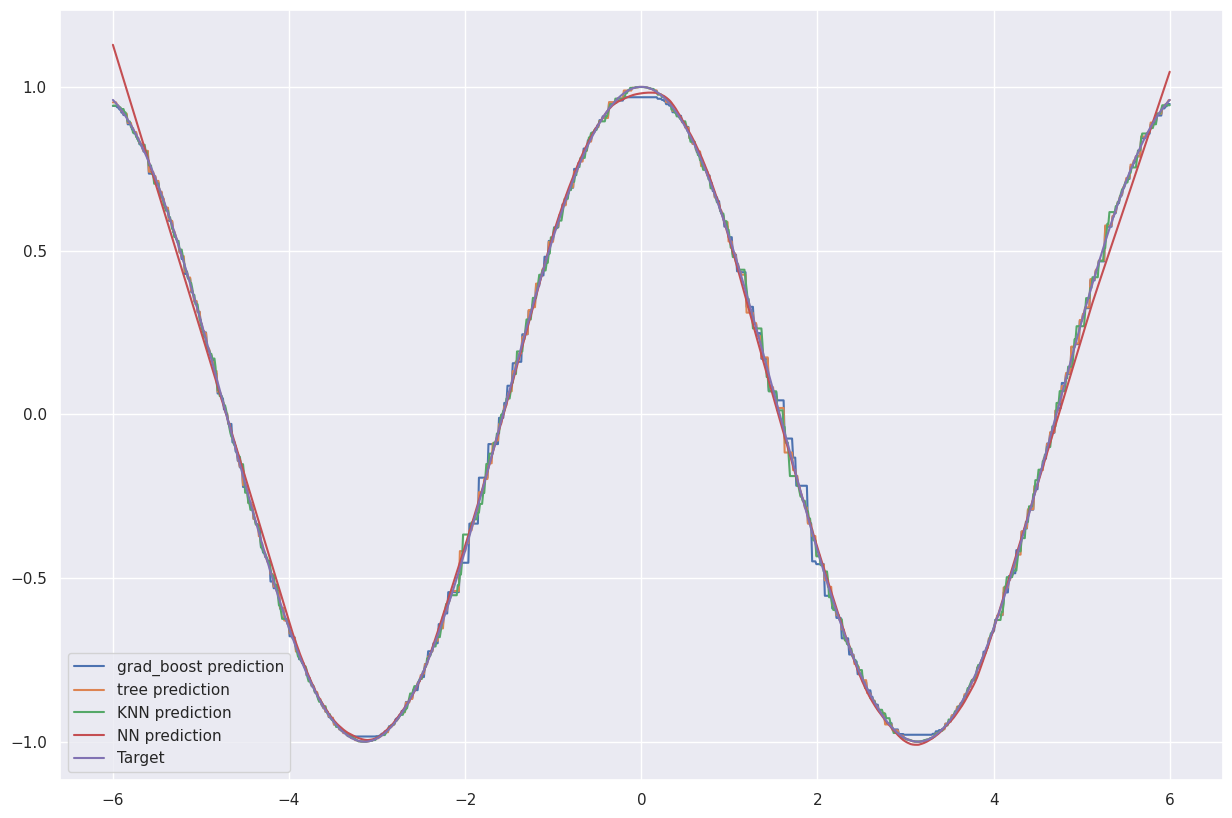
因此，神经网络是一种全新的模型，能够解决常见的监督学习问题。事实证明，神经网络也能够解决无监督学习问题。研究神经网络的科学领域被称为深度学习。

深度学习是一个庞大的知识领域。它包含许多与神经网络的构建和训练相关的具体方法和技术，以及一些相关的理论成果。

如今，神经网络的应用无处不在：

• 语音助手和翻译器

• 语音识别和生成

• 人脸识别

• 网络安全

• 无人机

• 黑洞探测

• 推荐系统、音乐和视频推荐

• 通过查询搜索猫咪照片 ~(=^‥)/

• 以及更多其他应用…

补充数学知识

在本节中，我们将介绍神经网络更严谨、更准确的定义。结合以上示例，读者现在应该更容易理解了。

定义： 一个具有 N 个神经元的全连接单层神经网络，是向量参数 $\vec{x}$（列向量）的函数，由参数矩阵 $W=(w_{ij})$ 参数化，其形式如下：$$NN(\vec{x})=f(W\cdot \vec{x})$$

这里的矩阵 W 的维度为 $N\times dim(\vec{x})$。函数 f 是一个任意函数，称为激活函数。这个名称源于神经网络模型最初主要与生理感知模型相关的时期，我们在本讲中已经讨论过该模型。在这种情况下，“激活”指的是神经元的激活。有很多标准的激活函数，我们将在下一讲中详细讨论。激活函数的一个例子是著名的 sigmoid 函数。

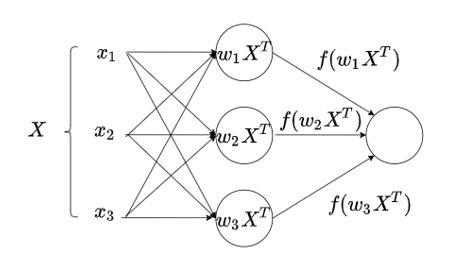
在这些并行变换中，我们将某个权重向量 ${\vec{w}}_i$ 与同一个输入向量 $\vec{x}$ 进行标量乘法，也就是说，得到的数集具有 $(({\vec{w}}_1,\vec{x})...({\vec{w}}_N,\vec{x}))$ 的形式。让我们思考一下：如果我们把所有向量 ${\vec{w}}_i$ 逐行写成一个矩阵，那么根据矩阵乘法的规则，$W\cdot \vec{x}$ 将是一个 $N\times 1$ 的列向量。这个输出向量中索引为 i 的分量将由矩阵 W 的第 i 行与 $\vec{x}$ 的标量积表示，即 $({\vec{w}}_i,\vec{x})$。因此，要获得所呈现层的输出，只需考虑矩阵乘积 $W\cdot \vec{x}$ 的结果集即可。

事实上，计算表达式 $\vec{x}\cdot W$ 也能得到相同的结果，但前提是向量 $\vec{x}$ 由行向量表示，且向量 $w_i$ 不是按行而是按列写入矩阵 W。只需分别逐个元素地写出矩阵乘积，即可轻松得出此结论。

最后一步是应用激活函数 f。这将得到向量 $(f({\vec{w}}_1,\vec{x})...f({\vec{w}}_N,\vec{x}))$。为简洁起见，将 f 分别应用于向量的每个分量，记为将 f 应用于整个向量：$$(f({\vec{w}}_1,\vec{x})...f({\vec{w}}_N,\vec{x}))=f(({\vec{w}}_1,\vec{x})...({\vec{w}}_N,\vec{x}))$$

在这种情况下，我们得到了神经网络定义中提出的此类变换的符号：$$NN(\vec{x})=f(({\vec{w}}_1,\vec{x})...({\vec{w}}_N,\vec{x}))=f(W\cdot \vec{x})$$

---

注意： 在此定义框架内，我们可以得到多个对象 $\vec{x}_1 …同时对 ${\vec{x}}_M$ 进行运算。为此，我们将这些向量逐列写入矩阵 $X$，并考虑表达式 $A=W\cdot X$。该矩阵乘积的结果是一个 N × M 矩阵。该矩阵的 $a_{ij}$ 坐标表示标量积 $({\vec{w}}_i,{\vec{x}}_j)$ 的结果，即对第 $j$ 个输入向量应用第 $i$ 个线性变换的结果。因此，矩阵 A 的列表示将单层神经网络独立应用于每个输入向量的结果。

定义： 多层神经网络是一种变换，它是 K 个单层神经网络的顺序应用，每个单层神经网络都将前一层的输出作为下一层的输入。在这个概念中，第一层称为输入层（通常假设它不执行任何变换，而只是“接收”输入向量），最后一层称为输出层。每个单层神经网络称为一个包含 N 个神经元的层。

例如，一个两层神经网络可以表示为如下变换：$$NN(X)=f_2(W_2\cdot f_1(W_1\cdot X))$$

一个三层网络：$$NN(X)=f_3(W_3\cdot f_2(W_2\cdot f_1(W_1\cdot X)))$$

以此类推。

NumPy 实现示例

让我们尝试用 NumPy 实现一个两层神经网络的结构。

import numpy as np
# 从神经网络的输入获取其输出通常称为前向传播。
# 我们将在前向函数中实现这一点。
def forward(W1, W2, X, f1, f2):
  z1 = np.matmul(W1, X)
  a1 = f1(z1)
  z2 = np.matmul(W2, a1)
  a2 = f2(z2)
  return a2

现在我们面临的问题是：如何训练神经网络？

我们需要选择最优参数矩阵 $W_1$ 和 $W_2$，以最小化某个误差函数 L。

我们将使用梯度下降算法来实现这一点。

import sklearn
from sklearn.datasets import load_breast_cancer
from sklearn.preprocessing import StandardScaler
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

X, y = load_breast_cancer(return_X_y=True)
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.33, shuffle=True)


Sc = StandardScaler()
x_train = Sc.fit_transform(x_train)
x_test = Sc.transform(x_test)

# 在 X 列的最后一列添加一列全为 1 的元素。这是为了添加自由项所必需的。
x_train = np.c_[x_train, np.ones(x_train.shape[0])]
x_test = np.c_[x_test, np.ones(x_test.shape[0])]

N_1 = 3
N_2 = 1

W1 = np.random.randn(N_1, x_train.shape[1])
W2 = np.random.randn(N_2, N_1)

def sigmoid(x):
  return 1/(1 + np.exp(-x))

f1 = sigmoid
f2 = sigmoid

forward(W1, W2, x_train[0].T, f1, f2)

输出：array([0.89454418])

本例中的梯度下降算法

我们希望将梯度下降算法应用于一个具体问题。例如，考虑一个二分类问题。

我们目前得到的答案没有意义。为了训练模型，我们将使用已经很熟悉的二元交叉熵函数。该函数由以下表达式定义：$$H(y,\hat{y})=-\frac{1}{N}\sum _{i=1}^N(y_i\cdot log(\widehat{y_i})+(1-y_i)log(1-\widehat{y_i}))$$

其中，$y_i$ 是正确答案，$\widehat{y_i}$ 是我们算法的假设，表示将对象 $x_i$ 分类为类别 1 的概率。

def BCE(y_pred, y_true):
    m = y_true.shape[0]
    loss = -1 / m * (np.dot(y_true, np.log(y_pred).T) + np.dot(1 - y_true, np.log(1 - y_pred).T))
    return np.squeeze(loss)

def uni_BCE(y_pred, y_true):
  return -(y_true*np.log(y_pred) + (1 - y_true)*np.log(1 - y_pred))

因此，我们现在的任务是在已知神经网络模型参数的情况下，计算函数 H 的梯度，其中 $\widehat{y_i}=a_2=NN({\vec{x}}_i)=\sigma (W_2\cdot \sigma (W_1\cdot {\vec{x}}_i))$。

使用前面引入的符号，$${\vec{z}}_1=W_1\cdot {\vec{x}}_i$$

$${\vec{a}}_1=\sigma ({\vec{z}}_1)$$

$${\vec{z}}_2=W_2\cdot {\vec{a}}_1$$

$$a_2=\sigma ({\vec{z}}_2)$$

其中所有向量均由列表示。在本例中，$a_2({\vec{x}}_i)={\hat{y}}_i$ 是一个标量。

让我们逐个分量地写出来：

$$(z_1{)}_i={\omega }_{i1}^1{x}_1+...+{\omega }_{iK}^1{x}_K$$

其中 K 是向量 $\vec{x}$ 的维度，${\omega }_{ij}^1$ 是矩阵 $W_1$ 的分量。向量 ${\vec{z}}_1$ 总共包含 L 个分量，其中 L 是第一层神经元的数量。

此外，在我们的例子中，$$z_2=W_2\cdot a_1={\omega }_1^2{a}_1^1+...+{\omega }_L^2{a}_L^1$$

$$a_2=\sigma (z_2)$$

那么 $$\frac{\partial H}{\partial {\omega }_i^2}=\frac{\partial H}{\partial a_2}\frac{\partial a_2}{\partial {\omega }_i^2}$$

$$\frac{\partial H}{\partial a_2}=-\frac{1}{N}\sum _{i=1}^N{y}_i\cdot \frac{1}{a_2({\vec{x}}_i)}-(1-y_i)\frac{1}{1-a_2({\vec{x}}_i)}$$

如果我们只考虑单个对象的导数x:

$$\frac{\partial H}{\partial a_2}=-(y\cdot \frac{1}{a_2}-(1-y)\frac{1}{1-a_2})$$

我们计算 $\frac{\partial a_2}{\partial {\omega }_i^2}$:

$$\frac{\partial a_2}{\partial {\omega }_i^2}=\frac{\partial \sigma ({\vec{z}}_2)}{\partial {\omega }_i^2}=\sigma ({\vec{z}}_2)(1-\sigma ({\vec{z}}_2))\frac{\partial {\vec{z}}_2}{\partial {\omega }_i^2}=a_2(1-a_2)a_i^1$$

这里我们使用了众所周知的 sigmoid 函数性质：${\sigma }^{\prime }=\sigma (1-\sigma )$

因此，我们用激活值 ${\vec{a}}_1$ 和 $a_2$ 表示了对第二层参数的导数。这引出了一个重要结论：在对对象进行预测计算时，这些值需要被缓存。对第二层参数的导数最终形式为：

$$\frac{\partial H}{\partial {\omega }_i^2}=-(a_2(1-a_2)a_i^1(y\cdot \frac{1}{a_2}-(1-y)\frac{1}{1-a_2}))=-{\alpha }_i^1((1-{\alpha }_2)y-{\alpha }_2(1-y))$$

现在我们求对第一层参数的导数

$$\frac{\partial H}{\partial {\omega }_{ij}^1}=\frac{\partial H}{\partial z_2}(\frac{\partial z_2}{\partial z_1^1}\frac{\partial z_1^1}{\partial {\omega }_{ij}^1}+...+\frac{\partial z_2}{\partial z_L^1}\frac{\partial z_L^1}{\partial {\omega }_{ij}^1})$$

反过来：

$$\frac{\partial z_2}{\partial z_k^1}={\omega }_k^2{a}_k^1(1-a_k^1)$$
和
$$\frac{\partial z_k^1}{\partial {\omega }_{ij}^1}=0,k\ne i$$
$$\frac{\partial z_k^1}{\partial {\omega }_{ij}^1}=x_j,k=i$$

然后：
$$\frac{\partial H}{\partial {\omega }_{ij}^1}=\frac{\partial H}{\partial z_2}\frac{\partial z_2}{\partial z_i^1}\frac{\partial z_i^1}{\partial {\omega }_{ij}^1}=\frac{\partial H}{\partial z_2}{\omega }_i^2{a}_i^1(1-a_i^1)x_j=-a_2(1-a_2)(y\cdot \frac{1}{a_2}-(1-y)\frac{1}{1-a_2}){\omega }_i^2{a}_i^1(1-a_i^1)x_j$$

由此，我们求出了损失函数对双层神经网络两层参数的导数。

读到这里，你们或许会疑惑：在为每个任务构建神经网络时，真的需要进行所有这些计算吗？

答案当然是否定的。否则，人类就永远无法训练出超过两层的神经网络，而有时神经网络的深度却会达到数十万层。有一种特殊的算法可以让我们快速计算每一层参数的导数。这种算法叫做反向传播算法，或者简称反向传播算法。我们将在下一讲详细讨论它。顺便说一句，对于那些已经掌握了上述计算的同学来说，这个算法应该很简单易懂。

现在，我们有一个绝佳的机会，可以用代码来实现所有这些计算。

# 需要向前重写，以便也能获取激活和预激活的缓存值
def forward(W1, W2, X, f1, f2):
  z1 = np.matmul(W1, X)
  a1 = f1(z1)
  z2 = np.matmul(W2, a1)
  a2 = f2(z2)
  return a2, (z1, a1, z2)

def grad_w2(a1: np.array, a2: float, y: int):
  L = a1.shape[0]
  dH = y*(1/a2) - (1 - y)*(1/(1 - a2))
  grad = a1.copy()
  grad = -dH*a2*(1 - a2)*grad
  return grad

def grad_w1(a1: np.array, a2: float, x: np.array, W2: np.array, y: int):
  dH = (y*(1/a2) - (1 - y)*(1/(1 - a2)))*a2*(1 - a2)
  mult = a1*(1 - a1)

  w2 = np.squeeze(W2)
  grad = np.zeros((w2.shape[0], x.shape[0]))
  for i in range(w2.shape[0]):
    for j in range(x.shape[0]):
      grad[i][j] = -mult[i]*dH*w2[i]*x[j]

  return grad

def train(W1, W2, X, y, num_epoch, learning_rate):
  for epo in range(num_epoch):
    epo_loss = []
    for i, x in enumerate(X):
      ans, cache = forward(W1, W2, x.T, sigmoid, sigmoid)
      z1, a1, z2 = cache
      grad_W1 = grad_w1(a1, ans, x, W2, y[i])
      grad_W2 = grad_w2(a1, ans, y[i])

      W1 = W1 - learning_rate*grad_W1
      W2 = W2 - learning_rate*grad_W2

      loss_ = uni_BCE(ans[0], y[i])

      epo_loss.append(loss_)
    print(f'Epoch {epo}. Loss: {np.mean(epo_loss)}')
  return W1, W2

W1, W2 = train(W1, W2, x_train, y_train, 120, 1e-3)

输出：

y_pred, _ = forward(W1, W2, x_test.T, sigmoid, sigmoid)
y_pred = y_pred.reshape(-1)

pred = (y_pred>0.5).astype(int)

from sklearn.metrics import accuracy_score
accuracy_score(pred, y_test)

输出：0.9202127659574468

我们利用双层神经网络实现了非常好的质量！