手撕红黑树

最新推荐文章于 2025-05-23 16:30:05 发布
最新推荐文章于 2025-05-23 16:30:05 发布
阅读量222 收藏
点赞数 1
分类专栏： 数据结构与算法 C++ 文章标签： 数据结构
版权声明：本文为博主原创文章，遵循 CC 4.0 BY-SA 版权协议，转载请附上原文出处链接和本声明。
本文链接：https://blog.youkuaiyun.com/supermario19/article/details/128693642
版权

一. 红黑树的定义

红黑树（Red Black Tree）是一种自平衡二叉查找树，红黑树插入，删除，查找都是O（logn）的时间复杂度。

二. 红黑树的性质

  1. 每个节点或红或黑

  1. 根结点为黑

  1. 每个叶子节点为黑

  1. 若一个节点为红，则它的孩子必须为黑

  1. 对每个节点，从该节点到其他子孙节点的所有路径上包含相同数目的黑色节点

第五条性质尤为重要，第五条性质表明红黑树不同于AVL树。红黑树平衡的是黑高，而AVL树平衡的是子树高度。

三. 红黑树的用途

  1. map, set底层采用红黑树进行存储

  1. 定时器

  1. Linux进程调度(CFS(Completely FairScheduler))

  1. Epoll的实现，内核会在内存中开辟一个空间存放epoll的红黑树，并将每个epollfd加入树中进行管理

四. 红黑树的插入

    • 红黑树节点旋转

红黑树在插入和删除过程中，由于破坏黑高，需要进行调整，而调整的过程中就会涉及到节点旋转的操作。可以说节点旋转是红黑树中非常重要的操作之一。

// 左旋操作
void RBtree::leftRotate(RBtree_node *x)
{
    RBtree_node *y = x->right;

    x->right = y->left;
    if (y->left != nil)
    {
        y->left->parent = x;
    }

    y->parent = x->parent;
    if (x->parent == nil)
    {
        root = y;
    }
    else if (x->parent->left == x)
    {
        x->parent->left = y;
    }
    else
    {
        x->parent->right = y;
    }

    y->left = x;
    x->parent = y;
}

// 右旋操作
void RBtree::rightRotate(RBtree_node *y)
{
    RBtree_node *x = y->left;

    y->left = x->right;
    if (x->right != nil)
    {
        x->right->parent = y;
    }

    x->parent = y->parent;
    if (y->parent == nil)
    {
        root = x;
    }
    else if (y->parent->left == y)
    {
        y->parent->left = x;
    }
    else
    {
        y->parent->right = x;
    }

    x->right = y;
    y->parent = x;
}

    • 红黑树插入节点

红黑树插入节点类似于二叉搜索树的插入，都是要先在树上寻找到合适的插入位置，再进行节点插入（插入叶子节点），只不过红黑树在插入结束之后要进行节点调整。所以在红黑树中插入节点有以下几个步骤：1. 寻找插入位置

2. 创建新节点

3. 插入，调整

// 节点插入
void RBtree::insert(KEY_TYPE key, VALUE_TYPE value)
{
    RBtree_node *pre = nil;
    RBtree_node *cur = root;

    // 寻找插入位置
    while (cur != nil)
    {
        pre = cur;
        if (key < cur->key)
        {
            cur = cur->left;
        }
        else if (key > cur->key)
        {
            cur = cur->right;
        }
        else
        {
            return;
        }
    }
    
    // 创建新节点
    RBtree_node *node = new RBtree_node(RED);
    node->key = key;
    node->value = value;
    node->left = nil;
    node->right = nil;
    node->parent = pre;

    // 新节点插入红黑树
    if (pre == nil)
    {
        root = node;
    }
    else
    {
        if (key < pre->key)
        {
            pre->left = node;
        }
        else
        {
            pre->right = node;
        }
    }
    
    // 插入调整
    insert_fixup(node);
}

    • 红黑树插入调整

若插入节点时，将插入节点颜色设置为黑色，插入红黑树中必定会将黑高平衡破坏，这样每次插入节点都会带来红黑树的调整。

若插入节点时，将插入节点颜色设置为红色，插入红黑树一定不会破坏黑高，但是会破坏性质4， 此时若插入节点父节点为红色节点，则需要进行调整。现在以插入节点的父节点为祖父节点的左孩子为例：

情况一：叔父节点为红色

此时将父亲节点染为黑色，叔父节点染为黑色，将祖父节点染为红色。之后从祖父节点开始继续向上迭代检查。

情况2：叔父节点为黑色，插入节点为父亲节点右孩子

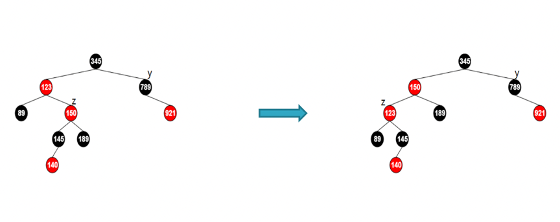
此时将以插入节点父节点为轴心进行左旋，此时转化为情况3

情况3. 叔父节点为黑色，插入节点为父亲节点左孩子。

此时将父节点染为黑色，将祖父节点染为红色，以祖父节点为轴型进行右旋。

// 插入修复
void RBtree::insert_fixup(RBtree_node *x)
{
    // 迭代检查父节点是否为红色，若为红色继续调整
    while (x->parent->color == RED)
    {
        // 当父节点为祖父节点左孩子
        if (x->parent == x->parent->parent->left)
        {
            // 叔父节点
            RBtree_node *y = x->parent->parent->right;

            // 情况1
            if (y->color == RED)
            {
                x->parent->color = BLACK;
                y->color = BLACK;
                x->parent->parent->color = RED;

                x = x->parent->parent;
            }
            else
            {
                // 情况2
                if (x == x->parent->right)
                {
                    x = x->parent;
                    leftRotate(x);
                }
                // 情况3
                x->parent->color = BLACK;
                x->parent->parent->color = RED;
                rightRotate(x->parent->parent);
            }
        }
        else
        {
            RBtree_node *y = x->parent->parent->left;
            if (y->color == RED)
            {
                x->parent->color = BLACK;
                y->color = BLACK;
                x->parent->parent->color = RED;

                x = x->parent->parent;
            }
            else
            {
                if (x == x->parent->left)
                {
                    x = x->parent;
                    rightRotate(x);
                }
                x->parent->color = BLACK;
                x->parent->parent->color = RED;
                leftRotate(x->parent->parent);
            }
        }
    }
    // 保证根节点一直为黑色
    root->color = BLACK;
}

五.红黑树的删除

    • 寻找一个子树上的最小节点和最大节点

RBtree_node *RBtree::mini_node(RBtree_node *x)
{
    while (x->left != nil)
    {
        x = x->left;
    }
    return x;
}

RBtree_node *RBtree::max_node(RBtree_node *x)
{
    while (x->right != nil)
    {
        x = x->right;
    }
    return x;
}

    • 寻找一个节点的后继节点

当寻找一个节点的后继节点时，存在两种情况：

情况1：该节点存在右子树，此时后继节点为右子树的最小值节点

情况2：该节点不存在右子树，此时后继节点为父节点不断迭代向上搜索，直到当前节点为父节点的左孩子节点，此时父节点为后继节点，例如13节点的后继节点为15

RBtree_node *RBtree::successor(RBtree_node *node)
{
    // 情况1
    if (node->right != nil)
    {
        return mini_node(node->right);
    }
    // 情况2
    else
    {
        RBtree_node *pre = node->parent;
        RBtree_node *cur = node;
        while (pre != nil && cur == pre->right)
        {
            cur = pre;
            pre = pre->parent;
        }
        return pre;
    }
}

    • 红黑树删除节点

红黑树删除时分为如下几种情况：

    • 该删除节点不存在左右子树

若遇到该情况，则直接删除节点

    • 删除节点存在右左子树或右子树

若遇到该情况，将该节点直接删除并且将左子树或右子树代替被删除节点位置。

    • 删除节点存在左子树且存在右子树

若遇到该情况，则寻找插入节点z的直接后继节点y，将y节点替换z节点值，最后删除y节点，y的右孩子连接y的父节点。

// 删除节点
void RBtree::erase(KEY_TYPE key)
{
    // y节点的孩子节点
    RBtree_node *x = nil;
    // 真正删除节点
    RBtree_node *y = nil;
    // 被覆盖节点
    RBtree_node *z = search_node(key);
    if (z == nil)
    {
        return;
    }
    // 情况1, 2
    if (z->left == nil || z->right == nil)
    {
        y = z;
    }
    else
    {
        // 情况3
        y = successor(z);
    }
    
    // x为y的左或右子树
    if (y->left != nil)
    {
        x = y->left;
    }
    if (y->right != nil)
    {
        x = y->right;
    }
    
    // 将x代替y的位置
    x->parent = y->parent;
    if (y->parent == nil)
    {
        root = x;
    }
    else if (y == y->parent->left)
    {
        y->parent->left = x;
    }
    else
    {
        y->parent->right = x;
    }
    
    // 将y值覆盖z值
    if (y != z)
    {
        z->key = y->key;
        z->value = y->value;
    }

    // 若删除节点y为黑色节点，则破坏黑高，进行调整
    if (y->color == BLACK)
    {
        erase_fixup(x);
    }
}

    • 红黑树删除节点调整

接上文，已知条件，y节点为黑色

调整节点为y节点的孩子节点x，若x节点颜色为红色，则直接将x节点染为黑色即可，此时不会破坏黑高。

调整节点为y节点的孩子节点x，若x节点颜色为黑色，此时破坏黑高，需要进行调整。

此时分为四种情况（以x节点为y节点左孩子节点为例）

情况1. 兄弟节点为红色：

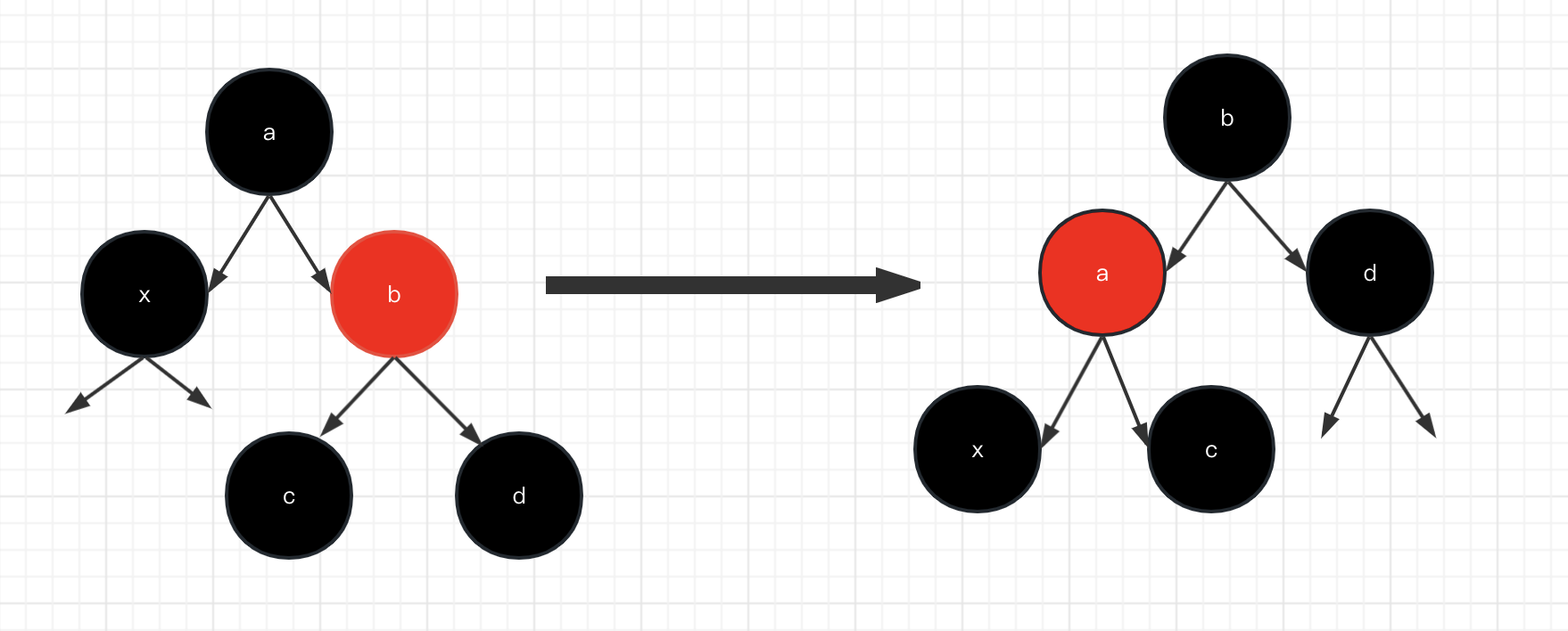
解决方法：将兄弟节点染为黑色，将父亲节点染为红色，进行左旋。

情况2：兄弟节点为黑色，且兄弟节点的左孩子右孩子节点都为黑色节点

解决方法：将兄弟节点染为红色

情况3. 兄弟节点为黑色，兄弟节点的左孩子为红色，右孩子为黑色

解决方法：此时将兄弟节点左孩子染为黑色，兄弟节点染为黑色，以兄弟节点为轴心进行右旋，转换为情况4

情况4.兄弟节点右孩子为红色

解决方法：将x父节点右孩子染为父节点颜色，x父节点染为黑色，兄弟节点右孩子染为黑色，以x父节点为轴心进行左旋，左旋结束之后结束循环。

void RBtree::erase_fixup(RBtree_node *x)
{
    while (x != root && x->color == BLACK)
    {
        if (x == x->parent->left)
        {
            RBtree_node *y = x->parent->right;
            // 情况1
            if (y->color == RED)
            {
                y->color = BLACK;
                x->parent->color = RED;
                leftRotate(x->parent);

                y = x->parent->right;
            }
            
            // 情况2
            if (y->left->color == BLACK && y->right->color == BLACK)
            {
                y->color = RED;
                x = x->parent;
            }
            else
            {
                // 情况3
                if (y->right->color == BLACK)
                {
                    y->color = RED;
                    y->left->color = BLACK;
                    rightRotate(y);

                    y = x->parent->right;
                }
                // 情况4
                y->color = x->parent->color;
                x->parent->color = BLACK;
                y->right->color = BLACK;
                leftRotate(x->parent);

                x = root;
            }
        }
        else
        {
            RBtree_node *y = x->parent->left;
            if (y->color == RED)
            {
                y->color = BLACK;
                x->parent->color = RED;
                rightRotate(x->parent);

                y = x->parent->left;
            }

            if (y->left->color == BLACK && y->right->color == BLACK)
            {
                y->color = RED;
                x = x->parent;
            }
            else
            {
                if (y->left->color == BLACK)
                {
                    y->color = RED;
                    y->right->color = BLACK;
                    leftRotate(y);

                    y = x->parent->left;
                }

                y->color = x->parent->color;
                x->parent->color = BLACK;
                y->left->color = BLACK;
                rightRotate(x->parent);

                x = root;
            }
        }
    }
    x->color = BLACK;
}

六. 完整代码

#ifndef RBTREE_H
#define RBTREE_H

typedef enum _COLOR
{
    BLACK = 0,
    RED = 1
} COLOR;

using KEY_TYPE = int;
using VALUE_TYPE = int;

class RBtree_node
{
public:
    KEY_TYPE key;
    VALUE_TYPE value;
    COLOR color;
    class RBtree_node *left;
    class RBtree_node *right;
    class RBtree_node *parent;

    RBtree_node(COLOR c)
        : color(c),
          key(-1),
          value(-1),
          parent(nullptr),
          left(nullptr),
          right(nullptr)
    {
    }
};

class RBtree
{
public:
    RBtree()
    {
        nil = new RBtree_node(BLACK);
        root = nil;
    }

    // 插入
    void insert(KEY_TYPE key, VALUE_TYPE value);

    // 删除
    void erase(KEY_TYPE key);

    // 寻找某个Key值是否存在
    bool find(KEY_TYPE key);

    // 层序遍历打印红黑树
    void print_level();

    // 中序遍历红黑树
    void print_middle();

private:
    // 左旋
    void leftRotate(RBtree_node *x);

    // 右旋
    void rightRotate(RBtree_node *y);

    // 插入修复
    void insert_fixup(RBtree_node *x);

    // 删除修复
    void erase_fixup(RBtree_node *x);

    // 查询某个key节点
    RBtree_node *search_node(KEY_TYPE key);

    // 寻找某个节点后继节点
    RBtree_node *successor(RBtree_node *node);

    // 寻找某颗子树上最小节点
    RBtree_node *mini_node(RBtree_node *x);

    // 寻找某颗子树上最大节点
    RBtree_node *max_node(RBtree_node *x);

private:
    RBtree_node *root;
    RBtree_node *nil;
};

#endif // RBTREE_H
#include "rbtree.h"
#include <iostream>
#include <queue>
#include <stack>

using namespace std;

void RBtree::insert(KEY_TYPE key, VALUE_TYPE value)
{
    RBtree_node *pre = nil;
    RBtree_node *cur = root;
    while (cur != nil)
    {
        pre = cur;
        if (key < cur->key)
        {
            cur = cur->left;
        }
        else if (key > cur->key)
        {
            cur = cur->right;
        }
        else
        {
            return;
        }
    }

    RBtree_node *node = new RBtree_node(RED);
    node->key = key;
    node->value = value;
    node->left = nil;
    node->right = nil;
    node->parent = pre;

    if (pre == nil)
    {
        root = node;
    }
    else
    {
        if (key < pre->key)
        {
            pre->left = node;
        }
        else
        {
            pre->right = node;
        }
    }
    insert_fixup(node);
}

void RBtree::erase(KEY_TYPE key)
{
    RBtree_node *x = nil;
    RBtree_node *y = nil;
    RBtree_node *z = search_node(key);
    if (z == nil)
    {
        return;
    }
    if (z->left == nil || z->right == nil)
    {
        y = z;
    }
    else
    {
        y = successor(z);
    }

    if (y->left != nil)
    {
        x = y->left;
    }
    if (y->right != nil)
    {
        x = y->right;
    }

    x->parent = y->parent;
    if (y->parent == nil)
    {
        root = x;
    }
    else if (y == y->parent->left)
    {
        y->parent->left = x;
    }
    else
    {
        y->parent->right = x;
    }

    if (y != z)
    {
        z->key = y->key;
        z->value = y->value;
    }

    if (y->color == BLACK)
    {
        erase_fixup(x);
    }
}

bool RBtree::find(KEY_TYPE key)
{
    RBtree_node *node = search_node(key);
    if (node != nil)
    {
        return true;
    }
    else
    {
        return false;
    }
}

void RBtree::print_level()
{
    if (root == nil)
    {
        return;
    }
    queue<RBtree_node *> q;
    RBtree_node *cur_end = root;
    RBtree_node *next_end = nullptr;
    q.push(root);
    int level = 1;

    while (!q.empty())
    {
        RBtree_node *node = q.front();
        q.pop();

        if (node != nil)
        {
            cout << "key:" << node->key << " value:" << node->value
                 << " color:" << (node->color == RED ? "RED" : "BLACK")
                 << " level:" << level << endl;
        }
        else
        {
            cout << "nil node"
                 << " level:" << level << endl;
        }

        if (node->left)
        {
            q.push(node->left);
            next_end = node->left;
        }
        if (node->right)
        {
            q.push(node->right);
            next_end = node->right;
        }

        if (node == cur_end)
        {
            if (cur_end != next_end)
            {
                level++;
            }
            cur_end = next_end;
        }
    }
}

void RBtree::print_middle()
{
    stack<RBtree_node *> s;
    RBtree_node *cur = root;
    while (cur != nil || !s.empty())
    {
        if (cur != nil)
        {
            s.push(cur);
            cur = cur->left;
        }
        else
        {
            RBtree_node *node = s.top();
            s.pop();
            cout << "key = " << node->key << "value = " << node->value << endl;
            cur = node->right;
        }
    }
}

void RBtree::leftRotate(RBtree_node *x)
{
    RBtree_node *y = x->right;

    x->right = y->left;
    if (y->left != nil)
    {
        y->left->parent = x;
    }

    y->parent = x->parent;
    if (x->parent == nil)
    {
        root = y;
    }
    else if (x->parent->left == x)
    {
        x->parent->left = y;
    }
    else
    {
        x->parent->right = y;
    }

    y->left = x;
    x->parent = y;
}

void RBtree::rightRotate(RBtree_node *y)
{
    RBtree_node *x = y->left;

    y->left = x->right;
    if (x->right != nil)
    {
        x->right->parent = y;
    }

    x->parent = y->parent;
    if (y->parent == nil)
    {
        root = x;
    }
    else if (y->parent->left == y)
    {
        y->parent->left = x;
    }
    else
    {
        y->parent->right = x;
    }

    x->right = y;
    y->parent = x;
}

void RBtree::insert_fixup(RBtree_node *x)
{
    while (x->parent->color == RED)
    {
        if (x->parent == x->parent->parent->left)
        {
            RBtree_node *y = x->parent->parent->right;
            if (y->color == RED)
            {
                x->parent->color = BLACK;
                y->color = BLACK;
                x->parent->parent->color = RED;

                x = x->parent->parent;
            }
            else
            {
                if (x == x->parent->right)
                {
                    x = x->parent;
                    leftRotate(x);
                }
                x->parent->color = BLACK;
                x->parent->parent->color = RED;
                rightRotate(x->parent->parent);
            }
        }
        else
        {
            RBtree_node *y = x->parent->parent->left;
            if (y->color == RED)
            {
                x->parent->color = BLACK;
                y->color = BLACK;
                x->parent->parent->color = RED;

                x = x->parent->parent;
            }
            else
            {
                if (x == x->parent->left)
                {
                    x = x->parent;
                    rightRotate(x);
                }
                x->parent->color = BLACK;
                x->parent->parent->color = RED;
                leftRotate(x->parent->parent);
            }
        }
    }
    root->color = BLACK;
}

void RBtree::erase_fixup(RBtree_node *x)
{
    while (x != root && x->color == BLACK)
    {
        if (x == x->parent->left)
        {
            RBtree_node *y = x->parent->right;
            if (y->color == RED)
            {
                y->color = BLACK;
                x->parent->color = RED;
                leftRotate(x->parent);

                y = x->parent->right;
            }

            if (y->left->color == BLACK && y->right->color == BLACK)
            {
                y->color = RED;
                x = x->parent;
            }
            else
            {
                if (y->right->color == BLACK)
                {
                    y->color = RED;
                    y->left->color = BLACK;
                    rightRotate(y);

                    y = x->parent->right;
                }

                y->color = x->parent->color;
                x->parent->color = BLACK;
                y->right->color = BLACK;
                leftRotate(x->parent);

                x = root;
            }
        }
        else
        {
            RBtree_node *y = x->parent->left;
            if (y->color == RED)
            {
                y->color = BLACK;
                x->parent->color = RED;
                rightRotate(x->parent);

                y = x->parent->left;
            }

            if (y->left->color == BLACK && y->right->color == BLACK)
            {
                y->color = RED;
                x = x->parent;
            }
            else
            {
                if (y->left->color == BLACK)
                {
                    y->color = RED;
                    y->right->color = BLACK;
                    leftRotate(y);

                    y = x->parent->left;
                }

                y->color = x->parent->color;
                x->parent->color = BLACK;
                y->left->color = BLACK;
                rightRotate(x->parent);

                x = root;
            }
        }
    }
    x->color = BLACK;
}

RBtree_node *RBtree::search_node(KEY_TYPE key)
{
    RBtree_node *node = root;
    while (node != nil)
    {
        if (key < node->key)
        {
            node = node->left;
        }
        else if (key > node->key)
        {
            node = node->right;
        }
        else
        {
            return node;
        }
    }
    return nil;
}

RBtree_node *RBtree::successor(RBtree_node *node)
{
    if (node->right != nil)
    {
        return mini_node(node->right);
    }
    else
    {
        RBtree_node *pre = node->parent;
        RBtree_node *cur = node;
        while (pre != nil && cur == pre->right)
        {
            cur = pre;
            pre = pre->parent;
        }
        return pre;
    }
}

RBtree_node *RBtree::mini_node(RBtree_node *x)
{
    while (x->left != nil)
    {
        x = x->left;
    }
    return x;
}

RBtree_node *RBtree::max_node(RBtree_node *x)
{
    while (x->right != nil)
    {
        x = x->right;
    }
    return x;
}

测试代码：

#include "rbtree.h"
#include <iostream>

int main()
{
    RBtree tree;
    for (int i = 0; i < 10; i++)
    {
        tree.insert(i, i);
    }
    tree.print_level();
    std::cout << "after erase" << std::endl;
    tree.erase(3);
    tree.print_level();
    tree.print_middle();
    return 0;
}

【数据结构进阶】手撕红黑树
2303_79329831的博客
08-01 1371
红黑树的介绍，以及底层代码逻辑和实现。刚刚接触编程的时候就听说有的大厂HR会让手撕红黑树。心中一直对这个数据结构保持着敬畏和向往，今天在将其撕出来后，用本篇博客加以记录，望周知。红黑树的结点包含四个成员变量，模板类型T：可以存储K或者pair类型，便于后期封装；三个指针：分别为指向左孩子结点的指针，指向右孩子结点的指针，指向父结点的指针；最后变量_col：枚举类型，可以存RED和BLACK。
数据结构：手撕红黑树(python方式)
Winnie_boy的博客
05-24 1141
前言：不知道同学有没有看完昨天的B树和B+树，虽说那个B+树在面试中很少被要求手写，但是有一个常考的考点，红黑树，可以一个经常被问到的知识噢，那么今天，我就来跟大家一起手撕红黑树！ 红黑树 说到红黑树不得不先提一下AVL树(平衡二叉搜索树)，不了解AVL树的同学可以自行查询相关文献，然后回来以后，请回答我的两个问题： 红黑树和AVL树的区别是什么？ 1.附上红黑颜色属性，通过颜色控制树的平衡 2.相对于AVL树来说，没有那么严格的要求平衡 3.插入和删除的复杂度和次数较AVL来说，跟随着数量节点的增大，越
红黑树增删操作详解
m0_48134027的博客
07-11 937
网上众多关于红黑树的讲解，但大多数都是重复的，只列出了几种简单情况，逻辑和思维深度都不足以解答吾之困惑。。。直到看到张彦峰先生的对红黑树的认识总结，基本可以说是集大成者，本文会基于此文章对复杂操作的思路方面做更详细的叙述和逻辑修正，但基本知识会略讲，可以参考原文或其它文章，原文中相关内容图片代码会直接引用，相信本文可以让你彻底弄懂RBTree的增删操作原理。
C++手撕红黑树
分享学习的知识，记录我的技术成长道路
08-07 711
红黑树在表意上就是一棵每个节点带有颜色的二叉搜索树，并通过对节点颜色的控制，使该二叉搜索树达到尽量平衡的状态。红黑树确保没有一条路径比其他路径长两倍。和AVL树不同的是，AVL树是一棵平衡树，而红黑树可能平衡也可能不平衡(因为是尽量平衡的状态)每一次插入都对根节点置为黑操作，因为第一种情况可能导致根节点不是黑。同时对根节点置黑也并不违反三条规定。...
【数据结构】手撕红黑树
学了就忘是正常现象
02-26 9256
红黑树和AVL树一样，因其逻辑复杂，面试时现场要求手撕就是纯纯刁难面试者。但某大厂面试官曾要求某些求职者现场手撕红黑树（我赌5毛，让面试官撕，他也撕不出来，而且你家员工上班手搓红黑树啊？），随后求职遭遇被发到网上吐槽，这便有了“手撕红黑树”的梗，也让红黑树成为了知名度最高的数据结构。（话虽如此，对于红黑树的性质、插入思想等概念还是需要掌握的）
深入浅出C++ ——手撕红黑树
weixin_55051736的博客
02-22 918
/节点的值域 Colour _col;//节点的颜色 RBTreeNode < K , V > * _left;//节点的左孩子 RBTreeNode < K , V > * _right;//节点的右孩子 RBTreeNode < K , V > * _parent;//节点的双亲 };
手撕红黑树-java版
YY3710YY的博客
08-04 381
手撕红黑树-java版 红黑树的五个平衡条件 每个节点非黑即红 根节点是黑色 叶节点（即虚拟叶节点，红黑树中的叶节点指的是看不见的虚拟空节点）是黑色 如果一个节点是红色，则它的两个子节点都是黑色的 从根节点出发到所有叶节点路径上，黑色节点数量相同 红黑树最长路径是最短路径的2倍 相比于AVL树，红黑树的控制条件更加松散，为了降低在插入和删除节点后的调整次数 红黑树自平衡的三种依据 变色：节点的颜色由黑变红或者由红变黑 左旋：已某一节点作为支点（旋转节点），其右子节点变为旋转节点的父节点，右子节点的左节
手撕红黑树代码（Java）
qq_52485934的博客
04-02 352
红黑树详细讲解，详细的源码讲解
【高阶数据结构】手撕红黑树（超详细版本）
qq_42996461的博客
01-08 2585
但行好事，莫问前程
【C++】——红黑树（手撕红黑树，彻底弄懂红黑树）
m0_74092462的博客
07-26 1752
我们之前都学过ALV树，AVL树的本质就是一颗平衡二叉树，它的作用就是查找，插入和删除节点，最坏的时间复杂度都是O(logn)的，同时维护的高度差都是小于等于1的，但是也就是因为这个原因才被红黑树所替代红黑树是一种自平衡的二叉查找树，是一种高效的查找树。它是由 Rudolf Bayer 于1978年发明，在当时被称为平衡二叉 B 树(symmetric binary B-trees)。后来，在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的红黑树。
【数据结构与算法】手撕红黑树
pythonxxoo的博客
04-02 899
Python微信订餐小程序课程视频 https://edu.youkuaiyun.com/course/detail/36074 Python实战量化交易理财系统 https://edu.youkuaiyun.com/course/detail/35475 红黑树 定义 动机： 二叉查找树查找、插入、删除最坏情况时间复杂度可能退化为 O(n)。 AVL 树很好的限制了数的高度为 O(logn)，插入、删除、查找的最坏时间复杂度均为 O(logn)；但删除操作最多需要做 O(logn) 次旋转。 红黑树是具有如下特点的二
【手撕红黑树 | 史上最详细注解】增删查改 原理剖析 代码实现
土味儿
09-14 286
1、基本特征 红黑树起源于2-3-4树(或2-3树)，底层是二叉查找树，除二叉树的特性外，还有5大特性： 根是黑色 节点是黑色或红色 叶子节点都是黑色 叶子节点为NIL节点，不可忽略，见下图 每个红色节点的两个子节点必须是黑色 从每个叶子到根的路径上不能有两个连续的红节点 黑色平衡 从任一节点到其所有叶子节点的简单路径上黑色节点数量相同 )] 2、内部节点类Node 双向链表：父 > 子 子 > 父 /** * 内部节点
Java手撕红黑树
wufeifan_learner的博客
01-07 856
前言 我这个人懒得不行，其实早就想学习学习红黑树了，以前只是知道这东西，也知道他是构成HashMap的底层数据结构（jdk1.8以后），但是每次一看红黑树的5条性质就头疼，不想去自习考虑这个数据结构。这个寒假终于下定决心用java手撕一遍红黑树，为了以后的面试做准备。由于这个数据结构有点庞大，我不想从基础开始讲解了，B站好多教学视频，我看了好多，但是现场手撕红黑树的，翻来翻去就那么几个。他们写代码的风格我不是太喜欢，且多是用的idea这个IDE，学生哪有钱买正版，我就直接用eclipse了，反正原理都一样，
Redis7 新增数据结构深度解析：ListPack 的革新与优化
希望我的博客，能帮上你解决学习中工作中所遇到的问题,也期待与您一起探讨技术问题，共同成长。
05-23 694
Redis 7.0引入了ListPack作为新一代序列化格式，替代了传统的ZipList，成为字符串、哈希、有序集合等数据类型的底层存储引擎。ListPack通过扁平化内存布局、高效的增删操作、优化的遍历机制和兼容性设计，显著提升了内存效率和访问速度。
自学嵌入式 day21 - 数据结构 双向链表
2301_81142331的博客
05-20 1136
双向链表，Makefile
数据结构 -- 交换排序（冒泡排序和快速排序）
最新发布
2202_75324779的博客
05-23 239
注：408原题中说，对所有尚未确定最终位置的所有元素进行⼀遍处理称为“⼀趟”排序，因此⼀次“划分”≠⼀趟排序。若每⼀次选中的“枢轴”将待排序序列划分为很不均匀的两个部分，则会导致递归深度增加，算法效率变低。基于“交换”的排序：根据序列中两个元素关键字的比较结果来对换这两个记录在序列中的位置。若每⼀次选中的“枢轴”将待排序序列划分为均匀的两个部分，则递归深度最⼩，算法效率最⾼。⼀次划分可以确定⼀个元素的最终位置，而⼀趟排序也许可以确定多个元素的最终位置。时间复杂度=O(n*递归层数)
【数据结构 -- AVL树】用golang实现AVL树
2401_87046050的博客
05-20 989
什么是AVL树，AVL树的思想，以及如何用go语言实现AVL树
Python的collections模块：数据结构的百宝箱
kymppcds的博客
05-20 1112
Counter用于统计可迭代对象中元素出现的频次。#统计次数#输出为：#使用update函数添加另一个可迭代对象，继续统计次数#输出为UserDict是创建自定义字典类的基类。raise NotImplementedError("删除操作不被允许")# 尝试删除键会引发错误继承UserDict并覆盖方法，可定制符合需求的字典类。类似UserDict，UserList用于创建自定义列表类。raise ValueError("只能添加整数")# 尝试添加非整数会引发错误。
红黑树与AVL树解析：网络工程师考前算法冲刺
“算法与数据结构-网络工程师考前冲刺100题”是一份针对网络工程师考试的复习资料，包含关于算法和数据结构的面试题，特别是关于红黑树和AVL树的知识。这份资料来源于牛客网，一个提供名企校招笔试面试真题的在线...
评论
添加红包

请填写红包祝福语或标题

个

红包个数最小为10个

元

红包金额最低5元

当前余额3.43元 前往充值 >
需支付：10.00元
成就一亿技术人!
领取后你会自动成为博主和红包主的粉丝 规则
hope_wisdom
发出的红包
实付元
使用余额支付
点击重新获取
扫码支付
钱包余额 0

抵扣说明：

1.余额是钱包充值的虚拟货币，按照1:1的比例进行支付金额的抵扣。
2.余额无法直接购买下载，可以购买VIP、付费专栏及课程。

余额充值