文章介绍了尾调用和尾递归的概念，指出尾递归在防止栈溢出方面的优势。递归虽然方便，但过度使用可能导致栈溢出，而尾递归由于只保留一个调用记录，能有效优化性能，尤其适用于解决需要递归的问题。
尾调用的概念和字面意思一致；
一句话就能说清楚，就是指某个函数的最后一步是调用另一个函数
如图所示：
尾递归的概念也是同上，字面意思就可以读到；
函数调用自身，称为递归。如果尾调用自身，就称为尾递归
那么使用场景会出自哪里呢？
我们最开始使用的是递归，递归的定义简单粗暴就是：
简单说程序调用自身的编程技巧叫递归
大白话就是：一层层套娃嵌套，拿到自己想要的数值就返回
然后层级递增，返回又是层级返回数值，就叫递归
递归函数能解决的场景包括不限于：
1.当问题和子问题具有递推关系，比如杨辉三角、计算阶乘
2.具有递归性质的数据结构，比如链表、树、图（例如树状图）
3.反向性问题，比如取反
递归函数的出现可以节省很多不必要的重复代码工作，但是相对应的也会有一些缺点，
在程序执行中，递归是利用堆栈来实现的。每当进入一个函数调用，栈就会增加一层栈帧，每次函数返回，栈就会减少一层栈帧。而栈不是无限大的，当递归层数过多时，就会造成 栈溢出 的后果
而为了解决该缺点，应运而生的就是今天要介绍的尾递归解决方法
定义：
函数调用自身，称为递归。如果尾调用自身，就称为尾递归。
递归非常耗费内存，因为需要同时保存成千上百个调用记录，很容易发生"栈溢出"错误。但对于尾递归来说，由于只存在一个调用记录，所以永远不会发生"栈溢出"错误
例如如图设置一个阶乘求值，如果是单纯的使用递归，就会导致每一次阶乘都会调用一次使用记录，每次执行都会调用外部变量的n，也就意味着消耗内存的同时还会导致“栈溢出”
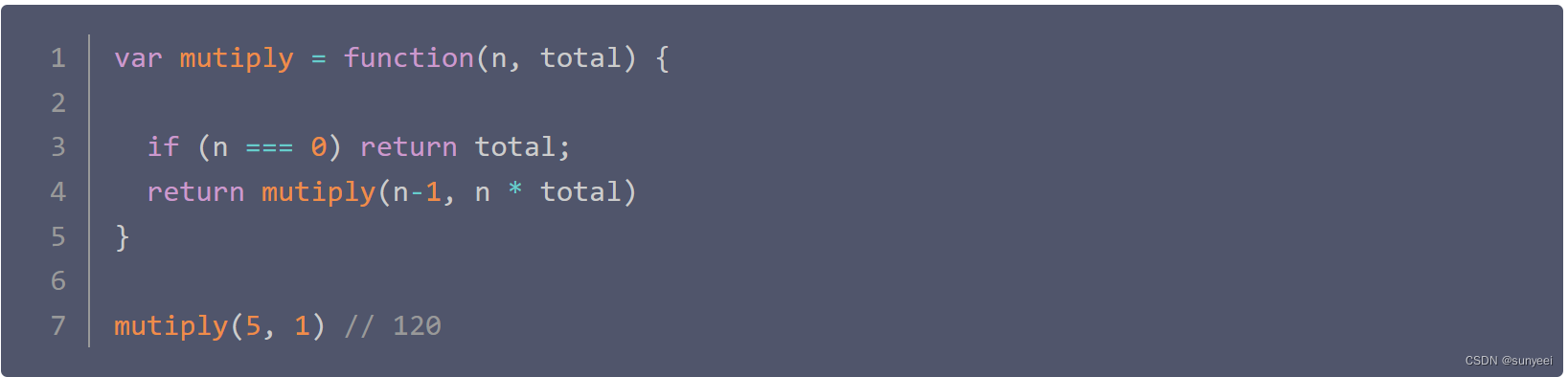
而当我们用到尾递归，就是将所有的操作放在一个函数进行执行，完全不需要担心每次调用都会产生调用记录，也不需要开辟新的“栈”，从而达到了优化性能的目的
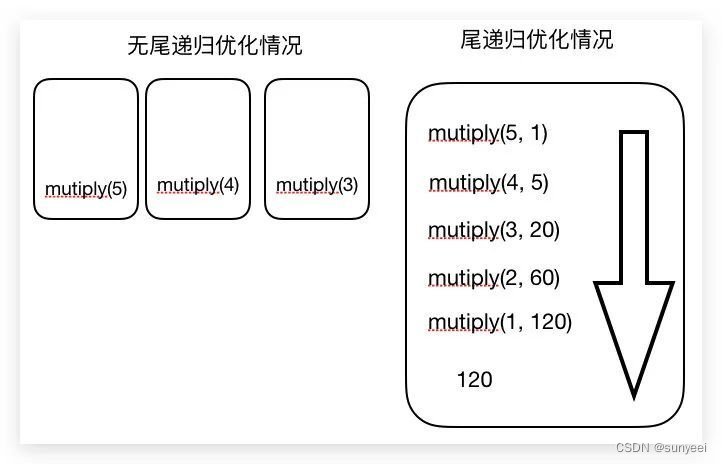
总而言之，尾递归是解决递归导致“栈溢出”的最优选
参考文章：
《阮一峰ES6入门》
扫一扫
被折叠的 条评论
为什么被折叠?
到【灌水乐园】发言
