[POJ1458]Common Subsequence(DP)

最长公共子序列问题解析

最新推荐文章于 2021-02-09 19:09:58 发布

原创最新推荐文章于 2021-02-09 19:09:58 发布 · 143 阅读

1 ·

CC 4.0 BY-SA版权

本文介绍了使用动态规划解决最长公共子序列问题的方法，并提供了一段C++代码实现。通过对比两个字符串，找出它们之间的最长公共子序列。推荐阅读《算法图解》一书以深入理解动态规划。

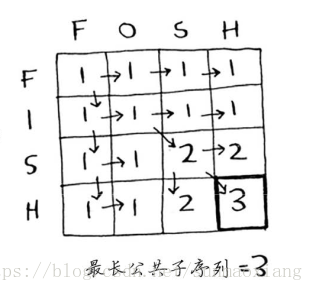
动态规划最经典的最长公共子序列问题，这里推荐一本书《算法图解》，里面讲LCS图文并茂～
这里写图片描述

#include <cstdio>
#include <cstring>
#include <algorithm>
#define MAXN 1000 + 10

char s1[MAXN];
char s2[MAXN];

int dp[MAXN][MAXN];

int main() {
    //freopen("input.txt", "r", stdin);
    while(~scanf("%s%s", s1, s2)) {
        int len1 = strlen(s1);
        int len2 = strlen(s2);
        memset(dp, 0, sizeof(dp));
        for(int i = 1; i <= len1; i++) {
            for(int j = 1; j <= len2; j++) {
                if (s1[i-1] == s2[j-1]) {
                    dp[i][j] = dp[i-1][j-1] + 1;
                }
                else {
                    dp[i][j] = std::max(dp[i-1][j], dp[i][j-1]);
                }
            }
        }
        printf("%d\n", dp[len1][len2]);
    }
    return 0;
}