线性模型--对数几率回归(逻辑回归)算法

对数几率回归

又常常称为逻辑回归，逻辑斯谛回归

如果是分类任务，如何使用线性回归模型呢？答案在广义线性模型的公式中，只需要找到一个单调可微函数将分类任务的真实标记y 与线性回归模型的预测值联系起来。

考虑二分类任务，输出 y∈{0,1}y \in \{0,1\}y∈{0,1} , 线性回归的预测值 $z=w^{T}x+b$ 是实值，需要对 z 进行转化，最理想的转换函数是单位阶跃函数，即预测值大于0时，判断正，小于0，判断负，等于0，则随机。但该函数是分段函数，是不连续函数，不符合广义线性模型中“联系函数”的要求，对数几率函数形似单位阶跃函数，但它是连续单调可微的。对数几率函数是一种“Sigmoid函数”，它预测值 z 转化为一个接近0或1的 y 值。

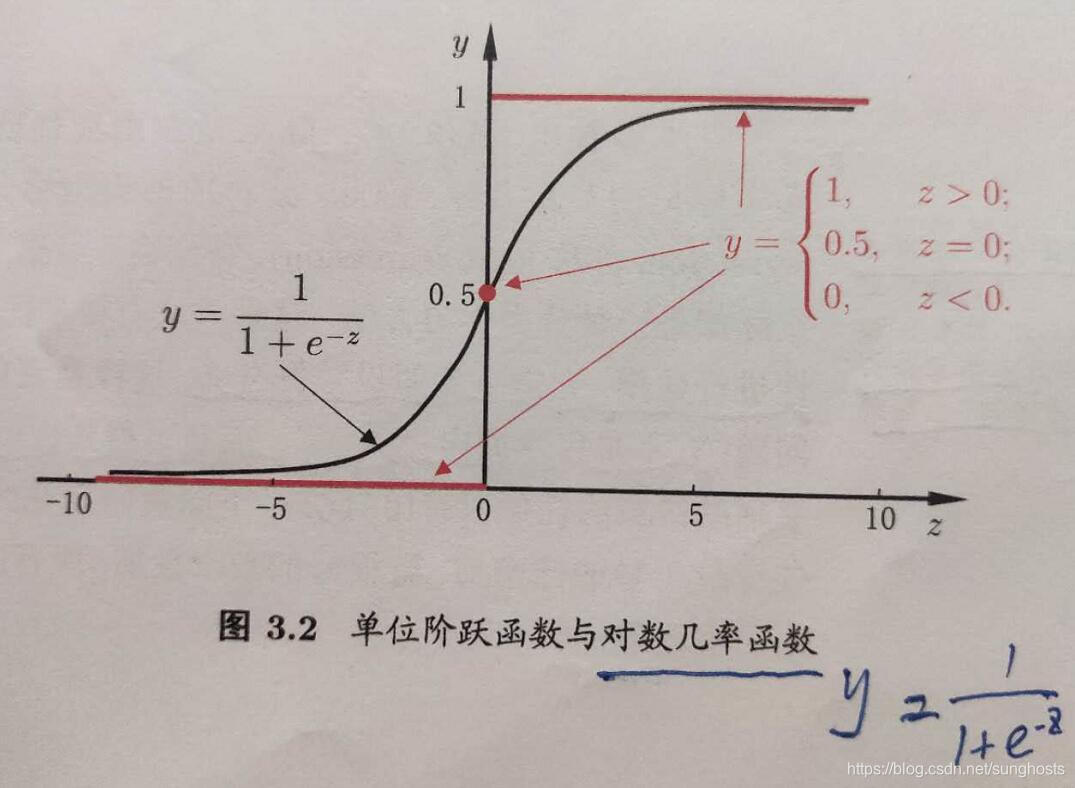
$$y=\frac{1}{1+e^{-z}}$$

代入广义线性模型公式得到

$$y=\frac{1}{1+e^{-(w^{T}x+b)}}$$

上述公式就是对数几率回归的公式。

这种分类方法有很多优点：它直接对分类可能性进行建模，无需事先假设数据分布；另外，不仅预测出“类别”，还得到了近似概率预测。它的目标函数是任意阶可导的凸函数，有很多数值优化算法，如牛顿法，拟牛顿法等都可用于求取最优解。

根据在线性回归中的讨论，对数几率回归公式可以写成如下形式(推导过程就不写了)：

$$\ln \frac{y}{1-y}=w^{T}x+b$$

将 y 视作类后验概率估计 $p(y=1|x)$, 上式写作

$$\ln \frac{p(y=1|x)}{p(y=0|x)}=w^{T}x+b$$

再加上两个概率和等于1的条件，显然有

$$p(y=1|x)=\frac{e^{w^{T}x+b}}{1+e^{w^{T}x+b}}$$

$$p(y=0|x)=\frac{1}{1+e^{w^{T}x+b}}$$

可通过“极大似然法”来估计 w 和 b 。

$$l(w,b)=\sum _{i=1}^{m}lnp(y_i|x_i;w,b)=\sum _{i=1}^{m}lnp(y_i|x_i;w,b)$$

上式就是对数几率回归的目标函数，最大化上述式子，可以通过梯度下降法、牛顿法等来求最优解。