Divide and Conquer

最新推荐文章于 2023-08-27 15:48:36 发布

原创最新推荐文章于 2023-08-27 15:48:36 发布 · 3.7k 阅读

0 ·

CC 4.0 BY-SA版权

Algorithms 专栏收录该内容

7 篇文章

订阅专栏

本文深入探讨了Divide and Conquer算法的概念、工作原理及在快速排序、归并排序、最近两点距离计算等算法中的应用，强调了算法选择的关键因素，并通过实例展示了算法的时间复杂度优化。

Divide and Conquer is an algorithmic paradigm based on multi-branched recursion.

A typical Divide and Conquer algorithm solves a problem using following three steps:

1. Divide: Break the given problem into subproblems of same type.
2. Conquer: Recursively solve these subproblems
3. Combine: Appropriately combine the answers

The name "divide and conquer" is sometimes applied also to algorithms that reduce each problem to only one subproblem, such as the binary search algorithm.

Because it uses tail recursion, so it can be converted into simple loops. Under this broad definition, however, every algorithm that uses recursion or loops could be regarded as a "divide and conquer algorithm". Therefore, some authors (I prefer this viewpoint too) consider that the name "divide and conquer" should be used only when each problem may generate two or more subproblems.The name decrease and conquer has been proposed instead for the single-subproblem class.

Divide and Conquer (D & C) vs Dynamic Programming (DP)
Both paradigms (D & C and DP) divide the given problem into subproblems and solve subproblems. How to choose one of them for a given problem? Divide and Conquer should be used when same subproblems are not evaluated many times. Otherwise Dynamic Programming or Memoization should be used. For example, Quicksort is a Divide and Conquer algorithm, we never evaluate the same subproblems again. On the other hand, for calculating nth Fibonacci number, Dynamic Programming should be preferred.

Following are some standard algorithms that are Divide and Conquer algorithms.

1) Quicksort is a sorting algorithm. The algorithm picks a pivot element, rearranges the array elements in such a way that all elements smaller than the picked pivot element move to left side of pivot, and all greater elements move to right side. Finally, the algorithm recursively sorts the subarrays on left and right of pivot element.

2) Merge Sort is also a sorting algorithm. The algorithm divides the array in two halves, recursively sorts them and finally merges the two sorted halves.

3) Closest Pair of Points The problem is to find the closest pair of points in a set of points in x-y plane. The problem can be solved in O(n^2) time by calculating distances of every pair of points and comparing the distances to find the minimum. The Divide and Conquer algorithm solves the problem in O(nLogn) time.

5) Strassen’s Algorithm is an efficient algorithm to multiply two matrices. A simple method to multiply two matrices need 3 nested loops and is O(n^3). Strassen’s algorithm multiplies two matrices in O(n^2.8974) time.

6) Cooley–Tukey Fast Fourier Transform (FFT) algorithm is the most common algorithm for FFT. It is a divide and conquer algorithm which works in O(nlogn) time.

5) Karatsuba algorithm for fast multiplication it does multiplication of two n-digit numbers in at most 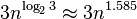$3 n^{\log_23}\approx 3 n^{1.585}$ single-digit multiplications in general (and exactly $n^{\log_23}$ when n is a power of 2). It is therefore faster than the classical algorithm, which requires n² single-digit products. If n = 2¹⁰ = 1024, in particular, the exact counts are 3¹⁰ = 59,049 and (2¹⁰)² = 1,048,576, respectively.