Few-Shot Learning with Graph Neural Networks

最新推荐文章于 2025-07-10 18:44:11 发布

原创

最新推荐文章于 2025-07-10 18:44:11 发布 · 7.1k 阅读

4 ·

CC 4.0 BY-SA版权

文章标签：

#GNN

本文探讨了在Few-Shot Learning场景下，如何使用图神经网络（GNN）进行图结构数据的学习。研究中，每个任务由部分标记的图像集合构成，通过构建全连接图并学习自适应相似度来推断未知标签。GNN层通过图卷积更新节点嵌入，以捕获图像之间的关系。此外，还介绍了一种基于CNN的边模型来学习边特征，增强模型的表达能力。

摘要生成于 C知道，由 DeepSeek-R1 满血版支持，前往体验 >

2 Related Work

meta-learners方式：典型代表是, Mishra et al. (2017) used Temporal Convolutions which are deep recurrent networks based on dilated convolutions(扩张卷积), this method also exploits contextual information from the subset T providing very good results.

deep learning architectures on graph-structured data领域： Graph neural networks(GNN) are in fact natural generalizations of convolutional networks to non-Euclidean graphs. 推荐阅读： We refer the reader to Bronstein et al. (2017) for an exhaustive literature review on the topic.

3 PROBLEM SET-UP

We consider input-output pairs (Ti, Yi)i drawn iid from a distribution P of partially-labeled image collections:

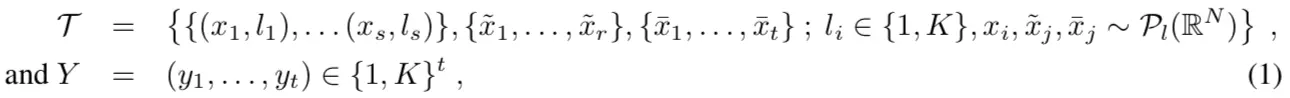
其中， s 即有label的样本数，r 即无label的样本数，t即待分类的样本数，K即分类类别数。

We will focus in the case t = 1 where we just classify one sample per task T .

Few-Shot Learning: When r = 0, t = 1 and s = qK, there is a single image in the collection with unknown label. If moreover each label appears exactly q times, this setting is referred as the q-shot, K-way learning.

4 MODEL

we associate T with a fully-connected graph GT = (V,E) where nodes va ∈ V correspond to the images present in T (both labeled and unlabeled). In this context, the setup does not specify a fixed similarity ea,a′ between images xa and xa′ , suggesting an approach where this similarity measure is learnt in a discriminative fashion with a parametric model similarly as in Gilmer et al. (2017), such as a siamese neural architecture. This framework is closely related to the set representation from Vinyals et al. (2016), but extends the inference mechanism using the graph neural network formalism that we detail next.